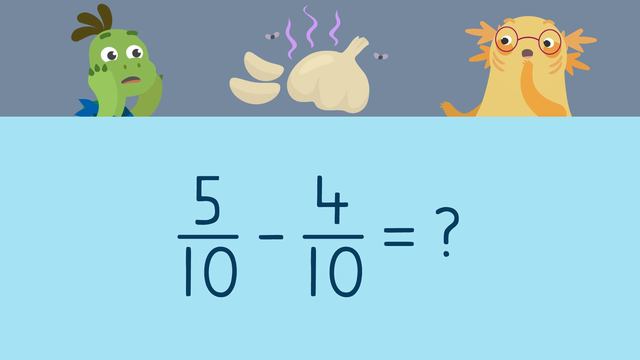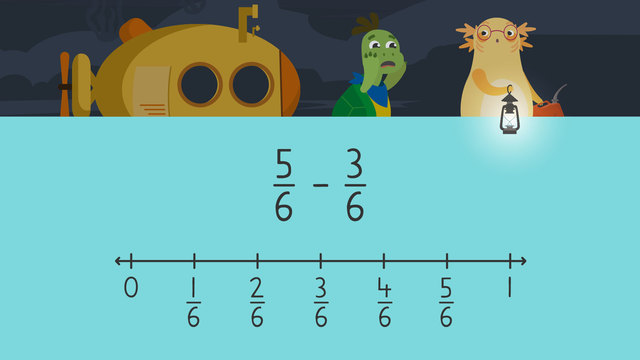Subtracting Fractions on a Number Line — Let's Practice!


Basics on the topic Subtracting Fractions on a Number Line — Let's Practice!
Today we are practicing subtracting fractions with Razzi! This video contains examples to help you further practice and grow confident in this topic.
Transcript Subtracting Fractions on a Number Line — Let's Practice!
Razzi says get these items ready, because today we're going to practice subtracting fractions on a number line. Using a number line, solve six eighths minus three eighths. Pause the video to work on the problem, and press play when you are ready to see the solution! Both denominators are eight, so divide the number line into eight equal parts. Now locate six eighths, which is here. Count back the numerator of the second fraction, which is three. Did you also get three eighths? Let's tackle the next problem! Using a number line, solve four fourths minus three fourths. Pause the video to work on the problem, and press play when you are ready to see the solution! Both denominators are four, so divide the number line into four equal parts. One whole is the same as four fourths, so start here. Count back the numerator of the second fraction, which is three. Did you also get one fourth? Let's tackle the final problem! Using a number line, solve two thirds minus two thirds. Pause the video to work on the problem, and press play when you are ready to see the solution! Both denominators are three, so divide the number line into three equal parts. Now locate two thirds, which is here. Count back the numerator of the second fraction, which is two. We land on zero, so we say the answer is zero. Did you also get zero? Razzi had so much fun practicing with you today! See you next time!
Subtracting Fractions on a Number Line — Let's Practice! exercise
-
Which number is the numerator?
HintsThe denominator is the bottom number in a fraction.
SolutionThe numerator in the fraction is the 1! The top number is the numerator and it will be very important in subtracting fractions!
-
Subtract these fractions and find the solution.
HintsHere is how the number line should look to solve the problem!
Since the problem is $\frac{7}{10}$ - $\frac{3}{10}$ you should start counting back from the fraction $\frac{7}{10}$!
SolutionThe correct answer is $\frac{4}{10}$! If you count back 3 points on the number line from $\frac{7}{10}$ you will see the answer is $\frac{4}{10}$!
-
Subtract these fractions and find the solution.
HintsHere is the number line you should use to solve the problem!
Since the problem is $\frac{4}{5}$ - $\frac{2}{5}$ you should start counting back from the fraction $\frac{4}{5}$!
Count back 2 from $\frac{4}{5}$!
SolutionThe correct answer is $\frac{2}{5}$! If you count 2 points back on the number line starting at $\frac{4}{5}$ you will see the answer is $\frac{2}{5}$!
-
Match the equations with the correct solutions.
HintsRemember, when subtracting fractions if the denominators are the same in the problem it will also be the same in the solution.
When using a number line to subtract, use the numerator (top number) in the second fraction to count backwards!
SolutionGreat job! Check your answers with the answers Razzi has in the image!
-
What is the missing numerator?
HintsHere is how your number line should look! Use this to help you solve the problem!
Start counting down from $\frac{9}{10}$!
Count back 5 from $\frac{9}{10}$!
SolutionThe correct answer is $\frac{4}{10}$! If you count 5 points back on the number line from $\frac{9}{10}$ you will see the answer is $\frac{4}{10}$! The 5 comes from the fraction $\frac{5}{10}$ in the problem.
-
What is the missing numerator?
HintsWe can use a number line to help us solve for the missing number too! Use this number line to help!
To solve for the missing number, we just need to find the difference between the numbers we do know. Subtract the smaller fraction from the larger fraction.
SolutionThe missing number is 4! We found this by subtracting $\frac{7}{8}$ - $\frac{3}{8}$ leaving us with the solution $\frac{4}{8}$.