Simple Interest
- Simple Interest – Definition
- Simple Interest Formula
- Calculating Simple Interest – Step-by-Step Process
- Finding Simple Interest – Practice
- Problem Solving with Simple Interest
- Solving for Principal ($P$)
- Solving for Time ($t$)
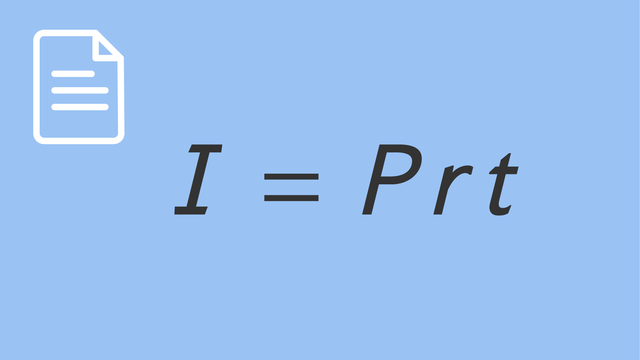

Basics on the topic Simple Interest
Simple Interest – Definition
When we talk about money, whether it's saving in a bank, borrowing for a car, or investing, interest often comes into play. Simple interest is a way to calculate the extra money earned or paid on a certain amount of money, called the principal, over a period of time. It's like a fee you pay for using someone's money or a reward for saving.
Simple interest is calculated using the formula $I = P \cdot r \cdot t$, where $I$ is the interest, $P$ is the principal amount, $r$ is the annual interest rate, and $t$ is the time. Understanding simple interest is crucial as it helps you calculate how much extra money you'll earn or need to pay on investments or loans, making financial planning more straightforward.
Simple Interest Formula
The formula used to calculate simple interest is the product of the principal amount, interest rate, and time. These three pieces of information must be known to find the simple interest.
Take a look at the meaning of each of these variables in the formula.
| Symbol | Meaning | Example |
|---|---|---|
| I | Interest earned or paid | - |
| P | Principal amount (initial money) | $200 |
| r | Annual interest rate (in decimal form) | 0.05 (5% ÷ 100) |
| t | Time the money is invested or borrowed (years) | 3 years |
Conversion of Percent to Decimal: To convert an interest rate from a percent to a decimal, divide by 100. For example, 5% becomes 0.05.
Understanding how to and being fluent in converting between percent, fractions and decimals is a skill that will help calculate simple interest.
Calculating Simple Interest – Step-by-Step Process
| Step | Action | Description |
|---|---|---|
| 1 | Identify Principal Amount (P) | Identify the principal amount (P), which is the initial amount of money. |
| 2 | Convert Rate to Decimal | Convert the interest rate from a percentage to a decimal by dividing by 100. |
| 3 | Determine Time Period (t) | Determine the time period (t) in years for which the interest will be calculated. |
| 4 | Use Simple Interest Formula | Use the simple interest formula $I = P r t$ to calculate the interest. |
| 5 | Calculate Total Amount | Calculate the total amount after interest by adding the principal amount and the interest earned. |
Finding Simple Interest – Practice
Practice finding the simple interest on your own.
Problem Solving with Simple Interest
The formula for calculating interest can also be used to problem-solve and work backward to find missing values, such as the principal, rate, or time.
Solving for Principal ($P$)
Given:
- Interest ($I$) = $\$150 $
- Interest rate ($r$) = 5% per year or 0.05 in decimal
- Time ($t$) = 3 years
We want to find the principal amount ($P$).
Rearrange the formula to solve for $P$: $P = \frac{I}{(r )( t)}$
Substitute in the values: $P = \frac{150}{(0.05)(3)} = \frac{150}{0.15} = 1000$
Answer: The principal amount is $\$$1000.
Solving for Time ($t$)
Given:
- Interest ($I$) = $\$200$
- Principal amount ($P$) = $\$1,000 $
- Interest rate ($r$) = 4% per year or 0.04 in decimal
We want to find the time ($t$).
Rearrange the formula to solve for $t$: $t = \frac{I}{(P)(r)}$
Substitute in the values: $t = \frac{200}{(1000)(0.04)} = \frac{200}{40} = 5$
Answer: The time is 5 years.
Now try more worded problems with various unknowns:
Simple Interest – Summary
Key Learnings from this Text:
- Simple interest is a straightforward way to calculate interest on a principal amount over time.
- The formula for simple interest is $\bf{I = P r t}$.
- The formula is also useful for finding missing information when the interest amount is already known.
- Always convert the interest rate from a percentage to a decimal before using the formula.
- The total amount after the interest period is the sum of the principal and the interest earned.
Simple Interest – Frequently Asked Questions
Transcript Simple Interest
Otter This World is known for its otterly awesome rides, and the Otter Viking Ship is no different. Hark! That noise can only mean one thing, those pesky weasels are "making it rain" again. Uh-oh...this time the weasels have gone too far. They've broken the machine! Luckily, Harriet, the park manager, notices this on CCTV, and puts in a call to a couple banks to get a quote on a loan so she can replace the broken ride. She calls the 1st National Beaver Bank, and the 2nd National Beaver Bank. The business beaver from the 1st Beaver Bank informs Harriet that he has an offer of a loan with a simple interest rate of 10% per year. The teller from the 2nd Beaver Bank counters with an attractive offer of 7% simple interest over 6 months. In order for Harriet to choose the best loan, and save some money, she'll have to understand simple interest. Let's help Harriet avoid paying more interest on the loan than she has to... What's a loan? A loan is money you can borrow from a bank for a given time period. The initial amount of money you borrow is called the principal. Of course, you need to pay this principal back in addition to the simple interest. Simple interest is the money you pay the bank to borrow the money. Harriet is requesting $5,000 in principal from the banks. The beaver banker from the 1st National Beaver Bank is offering a simple interest rate of 10% per year, while the beaver banker from the 2nd National Beaver Bank is offering a simple interest rate of 7% per six months. To calculate simple interest, you simply need to multiply the principal by the interest rate (in decimal form) by the length of time. In short form, this is written simply as 'i' equals 'p' 'r' 't'. As we said before, you not only need to pay the bank back the principal, but also the interest for the period of time you borrowed the money. Regardless of which bank Harriet borrows from, the principal is $5,000. Now we need to convert both of the interest rates to decimal form by dividing each percentage by 100. We get 0.1 for the first beaver bank and 0.07 for the second. The first bank's time period is already a year, so we can simply substitute 'one' for 't'. Also, since we want to compare the two interest rates, we should convert the second bank's time into years. Because 6 months happens twice a year we have to multiply the percentage, 0.07, by 2. If we plug in the numbers and multiply, we see that the interest owed to the first beaver bank at the end of a year is $500 and $700 for the second beaver bank. Great, let's review what we've learned. Harriet needs to get a loan from one of two beaver banks. The principal amount is $5,000. The simple interest rate from the 1st National Beaver Bank is 10% per year, which we calculated to be $500. The simple interest rate from the 2nd National Beaver Bank is 7% per 6 months, which sounds better at first, but which we calculated to be $700 per year. So if Harriet chooses the loan from the 1st bank with the 10% simple interest rate, she would owe the bank $5,500 at the end of the year. But if she chooses the 2nd Beaver Bank with the 7% simple interest over 6 months, she'd owe the bank $5,700 at the end of the year! Remember! If you want to compare two rates, make sure the time interval and units are the same! Sometimes, you might have to convert just like we did with the second bank's rate of 7% every 6 months. We can save Harriet $200 a year by going with the first beaver's offer! To find simple interest, you must multiply the principal times the decimal form of the rate, multiplied by the time in years. Harriet receives word that the repairs are done. And she scurries down to see the newly-repaired ride. Time for the big reveal... Let's see the new Otter Viking Ship! What in the world...!?!? Those weasels! What is this weasely ship?!
Simple Interest exercise
-
Understand the formula to find simple interest.
HintsThe formula for simple interest is calculated by multiplying the principal amount (the original amount of money) by the interest rate (the percentage charged or earned) and the time (how long the money is borrowed or invested).
The formula is expressed as:
Simple Interest = Principal × Rate ($r$) × Time ($t$)
For example, if you invest $100 (principal) at an interest rate of 5% per year for 3 years, the simple interest earned would be calculated as follows:
Simple Interest = $100 × 5% × 3 = $100 × 0.05 × 3 = $15
So, you would earn $15 in interest over 3 years.
Solution- Interest: The amount of money earned or paid for borrowing or lending money, calculated based on the principal, interest rate, and time.
- Principal: The original amount of money borrowed or invested.
- Rate: The percentage of the principal that is paid as interest per period.
- Time: The duration for which the money is borrowed or invested, typically in years.
-
Analyze the information in each problem to find the interest.
Hints$I$ = Interest: The amount of money earned or paid for borrowing or lending money, calculated based on the principal, interest rate, and time.
$P$ = Principal: The original amount of money borrowed or invested.
$r$ = Rate: The percentage of the principal that is paid as interest per period. This value is always given as a percent.
$t$ = Time: The duration for which the money is borrowed or invested, typically in years. This value is typically presented in years.
Solution1.) Principal = $500 Rate = 2% per year Time = 3 years
2.) Principal = $10 Rate = 1% per month Time = 6 months
3.) Principal = $15,500 Rate = 5% per year Time = 4 years
-
Calculate the simple interest.
HintsThe formula to find the simple interest is seen here.
- $I$ = Interest: The amount of money earned or paid for borrowing or lending money, calculated based on the principal, interest rate, and time.
- $P$ = Principal: The original amount of money borrowed or invested.
- $r$ = Interest Rate: The percentage of the principal that is paid as interest per period.
- $t$ = Time: The duration for which the money is borrowed or invested, typically in years.
The rate needs to be converted into a decimal.
To change a percent to decimal, divide by 100.
$2\%$ = $\frac{2}{100}$ = $0.02$
SolutionThe formula used is $I=Prt$
$P = 500$
$r = 2% = 0.02$
$t = 3$ years
The solution is:
$I = \bf{(500)(0.02)(3)}$
-
Understand the process to finding the simple interest of a real-world situation.
HintsTo change a percent to a decimal, divide the percent value by 100. Essentially, you are moving the decimal point two places to the left. For example, to convert $75\%$ to a decimal, divide $75$ by $100$, which equals $0.75$.
- $I$ = Interest: The amount of money earned or paid for borrowing or lending money, calculated based on the principal, interest rate, and time.
- $P$ = Principal: The original amount of money borrowed or invested.
- $r$ = Interest Rate: The percentage of the principal that is paid as interest per period.
- $t$ = Time: The duration for which the money is borrowed or invested, typically in years.
SolutionAri borrows $1,500 from a friend who charges them a simple interest of 4% per year. If Ari takes 2 years to pay back the loan, how much interest will they pay?
The formula used to find the interest is $\bf{I=Prt}$.
The principal amount that is borrowed is $\bf{\$1,500}$, the interest rate written as a decimal is $\bf{0.04}$, and the time period is 2 years.
When these values are substituted into the formula, the equation is $\bf{I=(1,500)(0.04)(2)}$.
After calculating, Ari will have accrued $120 in interest on top of the $1,500 they already owe back to their friend.
-
What is the formula to calculate simple interest?
HintsSimple interest is a way of calculating the interest you earn or pay on a loan or investment based on the original amount (principal), the interest rate, and the time the money is borrowed or invested.
The formula for simple interest is calculated by multiplying the original amount of money ($P$) by the percentage charged or earned ($r$) and then how many years the money is borrowed or invested ($t$).
Solution$I$ = Interest: The amount of money earned or paid for borrowing or lending money, calculated based on the principal, interest rate, and time.
$P$ = Principal: The original amount of money borrowed or invested.
$r$ = Rate: The percentage of the principal that is paid as interest per period.
$t$ = Time: The duration for which the money is borrowed or invested, typically in years.
-
Calculate the simple interest.
HintsUse the formula, $I=Prt$.
- $I$ = Interest: The money earned or paid from borrowing or lending, based on principal, rate, and time.
- $P$ = Principal: The initial amount borrowed or invested.
- $r$ = Rate: The percent of principal paid as interest per period.
- $t$ = Time: How long the money is borrowed or invested, usually in years.
SolutionTo find the interest earned, use the formula $I=Prt$.
$I=(3,000)(0.025)(3)$
$I$ = $225















