How to Read Complex Expressions

Basics on the topic How to Read Complex Expressions
Interpreting Algebraic Expressions
In this text, we're embarking on an adventure, but instead of battling monster llamas, we'll be tackling the world of algebraic expressions. Sharpen your pencils and put on your thinking caps because we're about to decode the language of algebra together!
Understanding Algebraic Expressions
An algebraic expression is a mathematical phrase that can include numbers, variables (like $x$ or $y$), and operation symbols. It's like a code that needs to be deciphered to understand the mathematical stories it tells.
These expressions can represent everything from simple quantities to complex relationships in equations. To help you become a code-cracking math-whiz, let's go over some vocabulary.
| Term | Operation | Description |
|---|---|---|
| Sum | Addition | Indicates adding two or more numbers together. |
| Difference | Subtraction | Signals the result of subtracting one number from another. |
| Product | Multiplication | Means the result of multiplying two or more numbers. |
| Quotient | Division | Refers to the result of dividing one number by another. |
Interpreting Algebraic Expressions – Examples
Example 1: Picture yourself in Aerial's boots, facing a puzzling expression: $3n + 6$ . The twist here is not to hastily read it from left to right. Instead, remember the golden rule: multiplication and division come before addition and subtraction, unless parentheses say otherwise.
Example 2: Aerial comes across another riddle: $3 - n \div 5$. She might misread it as "three minus $n$" first and then divide by five. Remember, prioritize division over subtraction. Writing division as a fraction helps in understanding the correct order.
Example 3: Our hero is faced with one last challenge: a verbal conundrum, "The quantity $x$ plus $8$, raised to the $4$th power." The term "quantity" clues us in that $x + 8$ is a group that we handle before applying the power of $4$.
Interpreting Algebraic Expressions – Practice
Reading and Interpreting Algebraic Expressions – Summary
Key Learnings from this Text:
- Algebraic expressions are codes made up of numbers, variables, and operations.
- Vocabulary like "sum," "difference," "product," and "quotient" gives clues on how to read expressions.
- Remember the order of operations: Multiplication and division come before addition and subtraction, with parentheses indicating priority.
- Translating words into algebraic expressions is a critical skill for solving mathematical problems.
Take the lessons from Aerial's story and apply them to your math adventures. The more you practice, the more confident you'll become in reading and interpreting these algebraic puzzles. And remember, this is just the beginning of your journey to becoming a math superhero!
Dare to explore more? Check out our interactive practice problems, videos, and worksheets on our educational platform. Your math hero journey continues!
Reading and Interpreting Algebraic Expressions – Frequently Asked Questions
Transcript How to Read Complex Expressions
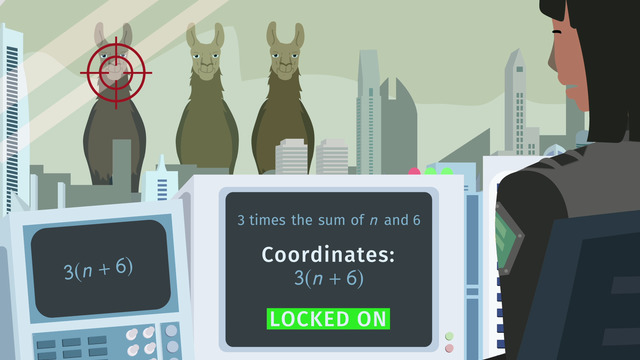
Megalopolis is on lockdown! Why? Every ten years, monster llamas, looking to graze, chow through the fields and forests surrounding Megalopolis. But this year, they're headed straight for the city! To fend off the llama monsters, the mayor of Megalopolis launches Neo-Hunter, a mecha for dealing with pretty much anything. But a new pilot, Aerial Earmath, has just completed her training and she’s a little unsure of how to work the guidance system. Luckily for Aerial, her robot friend, K2B2, will help her figure out how to read complex expressions so she can initiate the defense system.
First example - Addition and multiplication
Aerial sees an algebraic expression on the small monitor. To input the coordinates of the launch, she reads the expression: 3 times n plus 6. Oh no! That's wrong! An error message?! Her robot pal, K2B2, is trying to tell her something. In math, certain keywords - such as sum, difference, product and quotient tell you how the expressions are grouped. The correct way to read any algebraic expression is to distinguish what operation should be done and in what order. Thanks to K2B2, we know to group the addition before applying the multiplication and we're able to read the expression correctly, ‘3 times the sum of n and 6.’ Great work! The Neo-Hunter is now programmed to lock onto the correct coordinates but with no time to rest on her laurels Aerial gets another set of coordinates.
Second example - Subtraction and division
This time the expression includes division. At first, Aerial reads out the coordinates as, ’three minus n divided by 5.’ Oh no! Aerial didn't group the operations for this algebraic expression correctly. For fractions, we should read the numerator first, and then read the denominator. To help you stay organized when reading expressions, you can imagine that the numerator has parentheses around it, but it's not entirely necessary. For this example, the coordinates should be read: 'the quotient of the difference of 3 and n and 5.' Aerial thinks one more strike will get rid of the llamas for good.
Third example - Expression in written words
The next coordinate is an expression written out in words! We lucked out! All we have to do is read the expression and see what coordinates come out. ‘The quantity, x plus 8, raised to the 4th power.’ Let's start with what we know: 'x' plus 8. The word 'quantity' lets us know that this portion of the expression should be evaluated before any other operation is performed. In this case raising it to the 4th power. It worked! Neo-Hunter launches the projectiles of pizza? The city is saved! Hip, hip hooray! The llama monsters happily chow down.
How to Read Complex Expressions exercise
-
Explain how to read algebraic expressions out loud.
HintsKeep the parentheses in mind: there is a difference between $3(n+6)$ and $3n+6$.
In a fraction, you can also put the numerator or the denominator in parentheses:
$\frac{3-n}5=\frac{(3-n)}{5}$.
You first have to consider the term inside the parentheses.
For the order of operations remember:
- Paranthesis
- Exponent
- Multiplication
- Division
- Addition
- Subtraction
SolutionEach time we have to decide which operations should be done and the order in which they are done.
First, Aerial tries the following:
"Three times $n$ plus six!"
But, what's that? The login failed! Why?
The statement above stands for $3n+6$ without the parentheses. But there are parentheses around the sum of $n$ and $6$. So you have to read as follows:
"Three times the sum of $n$ and six."
In a similar way, if we read the second term as "Three minus $n$ over five“ then what we actually said was $3-\frac n5$.
So you have to show clearly that we are dividing a difference: "The quotient of the difference of 3 and $n$ and five."
-
Represent the given expression in an algebraic form.
Hints"... raise to the $4^{th}$ power" means $(~~~)^4$.
"plus" indicates addition ($+$).
There is a difference between $x^4+8^4$ and $(x+8)^4$.
You should read $x^4+8^4$ as follows:
"$x$ raised to the $4^{th}$ power plus $8$ raised to the $4^{th}$ power."
Solution"The quantity $x$ plus $8$, raised to the $4^{th}$ power."
What does this mean? Let's look at the expression step by step:
- "The quantity $x$ plus $8$" indicates addition. So we have $x+8$.
- "... raised to the $4^{th}$ power" means $(~~~)^4$.
Thus, we get the following algebraic expression: $(x+8)^4$.
-
Identify each algebraic expression with the correct way of reading it out loud.
HintsPay attention to the paranthesis.
Keep PEMDAS in mind for the order of operations.
- Paranthesis
- Exponent
- Multiplication
- Division
- Addition
- Subtraction
Here you see
"Three times the difference of $n$ and two."
SolutionFor transforming expressions in algebraic terms, we have to identify the operations as well as the order of those operations.
- $n-4\cdot 3$; the priority rule is Multiplication before Difference: "$n$ minus four times three."
- $5\cdot (n+4)$; the priority rule is Paranthesis before Multiplication: "Five times the sum of $n$ and four."
- $\frac{3+n}4$; the priority rule is Paranthesis before Division: "The quotient of the sum of three and $n$ and four".
- $\frac 3 4+n$; the priority rule is Divsion before Addition: "The quotient of three and four plus $n$."
-
Determine the right expression in written form for each of the given audio clips.
Hintsplus or sum indicate addition ($+$).
quotient or over stand for division ($\div$).
times indicates multiplication ($\times$).
- $3(n+4)$ can be read as "three times the sum of $n$ and four" or "three times the quantity of $n$ plus four".
- $3n+4$ can be read as "three times $n$ plus four".
SolutionLet's start with "Three times the sum of two times $x$ and three". We can see that "...the sum of two times $x$ and three" can be written as $2x+3$. Then we write three times this sum. To indicate the order we use parentheses around the sum: $3(2x+3)$.
Next we examine "the quotient of the sum of three and $x$ and the sum of two and $x$". "The quotient o...f" indicates $(~~~)\div(~~~)$. The numerator as well as the denominator are sums: $3+x$ and $2+x$. Together we get $\frac{3+x}{2+x}=(3+x)\div(2+x)$.
The last expression is "Three times $x$ plus two times the sum of $x$ and two". We have that "Three times $x$..." can be written as $3x$, "...the sum of $x$ and two" is $x+2$, and "...two times the sum of $x$ and two" is the algebraic term $2(x+2)$. Putting this all together gives us $3x+2(x+2)$.
-
Name keywords that indicate operations.
HintsYou can use numbers in algebraic operations: $5+6$.
You can also multiply numbers by variables: $5\times x$.
Keep the following terms in mind:
- summand $+$ summand $=$ sum
- minuend $-$ subtrahend $=$ difference
- factor $\times$ factor $=$ product
- dividend $\div$ divisor $=$ quotient
SolutionTo transform a given expression in an algebraic term, we first have to decide which operations are used.
There are a lot of keywords indicating the use of an operation:
- sum or plus indicate addition: $+$
- difference indicates subtraction: $-$
- times indicates multiplication: $\times$
- quotient indicates division: $\div$
-
Find the right audio clip(s) for the expression.
HintsYou can read a fraction as "the quotient of ... and ...", or as "the quotient of ... over ....".
- Three times the sum of $x$ and two can be written as $3(x+2)$.
- Three times $x$ and two can be written as $3x+2$.
Keep the order of operations as well as paranthesis in mind.
SolutionLet's start with the left part: it's a fraction with a sum in the numerator and a difference in the denominator:
- $3x+4$ can be read as "three $x$ plus four", or "the sum of three $x$ and four"
- $x-5$ is "the difference of $x$ and five", or "$x$ minus five"
Next we consider the right term, $-5(2x-3)$, which can be read as "minus five times the difference of two $x$ and 3".
Now we can put those parts together to get,
"The quotient of the sum of three $x$ and four and the difference of $x$ and five minus five times the difference of two $x$ and three",
or
"The sum of three $x$ and four over the difference of $x$ and five minus five times the difference of two $x$ and three".











