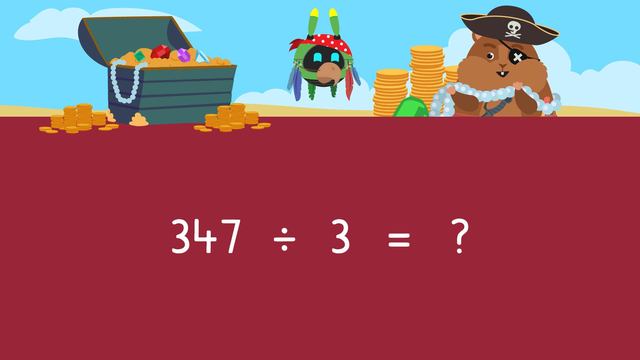Division with Remainders (Area Models) — Let's Practice!
- Understanding Division with Remainders Using Area Models – Introduction
- What Is Division with Remainders Using Area Models?
- Solving Division Problems with Remainders Using Area Models – Example
- Understanding Division with Remainders Using Area Models – Guided Practice
- Using Division with Remainders Using Area Models – Application
- Solving Division Problems Using Area Models – Summary
- Solving Division Problems Using Area Models – Frequently Asked Questions


Basics on the topic Division with Remainders (Area Models) — Let's Practice!
Understanding Division with Remainders Using Area Models – Introduction
We're diving into the world of division with remainders using area models. This method helps us visualize division and understand how remainders work. Get ready because today, we're going to practice this together!
What Is Division with Remainders Using Area Models?
Division with remainders using area models involves breaking down a division problem into smaller, more manageable parts and using an area model to visualize the process. This method helps us see how the numbers are divided and where the remainder comes from.
Here are the steps to tackle division with remainders using area models:
| Step # | Action |
|---|---|
| 1 | Identify the total number to be divided. |
| 2 | Use multiplication to create sections with an area model. |
| 3 | Subtract each section from the total number. |
| 4 | Continue until the remainder is less than the divisor. |
| 5 | Combine the results to find the quotient and the remainder. |
| 6 | Check your answer to ensure it makes sense with the problem. |
Let's practice understanding this method with a few examples.
Solving Division Problems with Remainders Using Area Models – Example
Example 1:
Problem: Use an area model to solve $ 86 ÷ 7$ .
Steps to Solve the Problem:
| Step # | Action | Description |
|---|---|---|
| 1 | Identify the total number to be divided. | 86 |
| 2 | Multiply $ 7 × 10$ . | 70 |
| 3 | Subtract 70 from 86. | 86 - 70 = 16 |
| 4 | Carry the 16 over. | 16 |
| 5 | Multiply $ 7 × 2$ . | 14 |
| 6 | Subtract 14 from 16. | 16 - 14 = 2 |
| 7 | The remainder is 2. | 2 |
| 8 | Add the results. | 10 + 2 = 12 |

Solution: The quotient is 12 remainder 2.
Example 2:
Problem: Use an area model to solve $ 527 ÷ 4$ .
Steps to Solve the Problem:
| Step # | Action | Description |
|---|---|---|
| 1 | Identify the total number to be divided. | 527 |
| 2 | Multiply $ 4 × 100$ . | 400 |
| 3 | Subtract 400 from 527. | 527 - 400 = 127 |
| 4 | Carry the 127 over. | 127 |
| 5 | Multiply $ 4 × 30$ . | 120 |
| 6 | Subtract 120 from 127. | 127 - 120 = 7 |
| 7 | Carry the 7 over. | 7 |
| 8 | Multiply $ 4 × 1$ . | 4 |
| 9 | Subtract 4 from 7. | 7 - 4 = 3 |
| 10 | The remainder is 3. | 3 |
| 11 | Add the results. | 100 + 30 + 1 = 131 |

Solution: The quotient is 131 remainder 3.
Understanding Division with Remainders Using Area Models – Guided Practice
Take a look at this problem: Use an area model to solve $ 68 ÷ 5$ .
In number sentence form: 68 ÷ 5 = 13 R3
Using Division with Remainders Using Area Models – Application
Now it's your turn. Solve these problems on your own.
Use an area model to solve $ 93 ÷ 6$ .
In number sentence form: 93 ÷ 6 = 15 R3
Solving Division Problems Using Area Models – Summary
Key Learnings from this Text:
- Solving problems using an area model can be achieved by following these steps:
| Step # | Action |
|---|---|
| 1 | Identify the total number to be divided. |
| 2 | Use multiplication to create sections of the area model. |
| 3 | Subtract each section from the total number. |
| 4 | Continue until the remainder is less than the divisor. |
| 5 | Combine the results to find the quotient and remainder. |
| 6 | Check your answer to ensure it makes sense with the problem. |
- Mastering the use of an area model for division with remainders is an important foundational math skill.
Keep practicing these steps, and you'll become a pro at using an area model to divide numbers with remainders! Check out more fun math challenges and exercises on our website to continue sharpening your skills.
Solving Division Problems Using Area Models – Frequently Asked Questions
Transcript Division with Remainders (Area Models) — Let's Practice!
Razzi says get these items ready, because today we're going to practice division with remainders, area models. It's time to begin! Use an area model to solve eighty-six divided by seven. Pause the video to work on the problem, and press play when you are ready to see the solution! Seven times ten equals seventy. Eighty-six minus seventy is sixteen. Carry the sixteen over. Seven times two equals fourteen. Sixteen minus fourteen is two, which is the remainder. Ten plus two equals twelve. Add the remainder, two. Did you also get twelve remainder two? Let's tackle one more problem! Use an area model to solve five hundred twenty-seven divided by four. Pause the video to work on the problem, and press play when you are ready to see the solution! Four times one hundred equals four hundred. Five hundred twenty-seven minus four hundred is one hundred twenty-seven. Carry the one hundred twenty-seven over. Four times thirty equals one hundred twenty. One hundred twenty-seven minus one hundred twenty is seven. Carry the seven over. Four times one equals four. Seven minus four is three, which is the remainder. One hundred plus thirty plus one is one hundred thirty-one. Add the remainder, three. Did you also get one hundred thirty-one remainder three? Razzi had so much fun practicing with you today! See you next time!
Division with Remainders (Area Models) — Let's Practice! exercise
-
Find the remainder of a division problem.
HintsTo complete the first section of the division diagram, we multiply $6 \times 4$ to get $24$, subtract this from $35$ to get a remainder of $11$, which carries over to the next box in the diagram.
In the second box on the diagram, there is a ?. What is $11 - 6$? This is the number which should be where the ? is.
Once you've figured out what $11-6$ is for the first ?, you should notice you cannot divide this by a multiple of $6$ any more so this is also the remainder for the overall calculation.
SolutionThe remainder for $35 \div 6$ is $5$. Look at the complete area model to see how $6$ divides into $35$, $5$ times and leaves a remainder of $5$.
-
Complete the calculation.
HintsFor the first box, what is $5 \times 4$? You could also figure out this box by working out the answer to the problem $27 -$? = $7$.
How many whole multiples of $4$ will divide into 7? This will help you with the box at the top of the area model diagram.
For the missing box closest to the bottom of the area model diagram, what is $7-4$? It is also the same number as the overall remainder for this problem.
How many whole multiples of $4$ will fit into $27$? This number will be your answer for the final box on the right side of the area model diagram.
SolutionLook at the worked solution of the area model to help with the division problem. $27 \div 4 = 6r3$.
-
Match the division sums with their corresponding answers and remainders.
HintsHave a look at the completed area model for the calculation $25 \div 7$ to give you a place to start. You'll notice that $2$ lots of $7$ were subtracted out first and then another single multiple of $7$ was able to be divided out giving a final solution of $3$ r $4$.
Here is another worked solution for the sum $18 \div 4$ to help you solve this question. In this question, $4$ lots of $4$ can be divided out leaving a remainder of $2$ which cannot have any more multiples of $4$ divided out any further.
This is another worked example of the sum $32 \div 6$ to help you find the matching pairs. $5$ multiples of $6$ can be divided out leaving us a remainder of $2$.
SolutionThe correct matching pairs are as follows;
- $18 \div 4 = 4 r 2$
- $25 \div 7 = 3 r 4$
- $31 \div 6 = 5 r 2$
- $28 \div 5 = 5 r 3$
-
Sort the steps into the correct order.
HintsWe use area models to help us with division calculations and working out remainders but also to help us break calculations down into smaller, more manageable steps.
When calculating a division, you would look for how many whole multiples divide into the number. The amount left over is the remainder.
SolutionThe correct order for the steps is;
1.) When completing the calculation $38 \div 9$ you can use a method such as an area model to help you break the problem down into smaller, more manageable steps.
2.) Find a multiple of $9$ that divides $38$ a whole number of times. For example, choose $3$, since $9 \times 3 = 27$ and $38 - 27 = 11$. Show this in the first box of the area model diagram.
3.) Next, focus on the current remainder, which is $11$ in this example. Notice that you can divide this by another multiple of $9$. This calculation goes into the second box of the area model, showing $9 \times 1 = 9$, so $11 - 9 = 2$.
4.) There are $4$ multiples of $9$ in $38$ with a remainder of $2$. Thus, $38 \div 9 = 4 $, r $2$.
-
Choose the correct answer.
HintsBy adding the two digits on the top of the area model diagram, $5+2$ you will get how many whole multiples of $6$ divide into $47$ and the first whole number to add to the diagram.
If you focus on the second box of the area model diagram and figure out the subtraction, $17-12$, this will be the remainder of the overall division sum and the second missing number.
Sometimes it can help to do the calculation from scratch, following the area diagram model method, instead of trying to pick it up midway from someone else's work.
SolutionThe correct solution for $47 \div 6$ is $7$ r $5$.
-
Sort the calculations.
HintsThere are two approaches to this task: either go through each calculation one by one or scan for those that are part of common times tables and won't result in a remainder.
Use an area model diagram, like we've done before, to determine which questions have remainders. Look at this example to see how.
Is it easier to start with the smaller divisor questions like $27 \div 5$ or $20 \div 4$?
SolutionThe calculations which have a remainder are;
- $27 \div 5$ as the answer is $5$ r $2$.
- $38 \div 9$ as the answer is $4$ r $2$.
- $50 \div 7$ as the answer is $7$ r $1$.
- $20 \div 4$ as the answer is $5$.
- $36 \div 6$ as the answer is $6$.
- $45 \div 9$ as the answer is $5$.