Division with Remainders (Area Models)
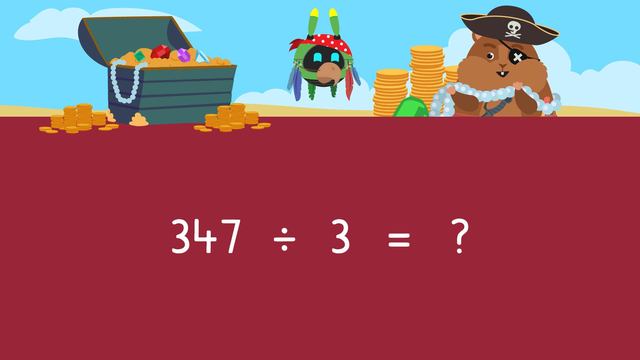

Basics on the topic Division with Remainders (Area Models)
Division with Remainders (Area Model)
Sometimes in division, you are left with a remainder. Imagine this: You’ve collected candy on Halloween with your friends and now you want to split up the candy evenly. You can visualize this division problem using an area model. In this text, you will learn how to use an area model with division and remainders.
Area Models in Division Problems – Example
You can use an area model for division with remainders by following some steps. Let’s practice with fifty-nine divided by five. These are the steps to follow in order to do division with remainders using an area model.
- Step 1: divide the area model
- Step 2: Write the divisor on the left side
- Step 3: Find a multiple close to the dividend
- Step 4: Subtract the product and carry the leftover
- Step 5:Add the numbers for the quotient, followed by the remainder (R).
First, set up an area model with columns matching the number of place values of the dividend. Fifty-nine has two place values, so set up an area model with two columns.
Next, put the divisor, five, on the left side, and write fifty-nine inside the first column.
It is usually easier to multiply by tens first, so write a ten above the first column.
Now multiply ten by the divisor, five, which is fifty. We need to subtract fifty from fifty-nine, which is nine.
Then, bring the nine over to the next column. This time, think how many times does five go into nine. It goes one time, so write one above the column.
Next, multiply five by one, which is five, and subtract this from the nine, which leaves us with four.
Since five cannot go into four, this will be the remainder. We add the ten and one at the top of the columns for the quotient, and add R 4 for the remainder.
Area Models in Division with Remainders – Review
Follow these steps to do division with area models:
| Step # | What to do |
|---|---|
| 1 | Divide the area model to match the number of place values in the dividend. |
| 2 | Write the divisor on the left side. |
| 3 | Find a multiple of the divisor that is close to, but doesn't go over the dividend. |
| 4 | Subtract the product from the dividend and carry the leftover to the next column. |
| 5 | Step 5 - Add the numbers above the columns for the quotient, then write (R) followed by the remainder. |
Want some more practice? After watching the video, you can find interactive exercises, worksheets and more activities on dividing with area models and remainders.
Transcript Division with Remainders (Area Models)
Mr. Squeaks and Imani have been on a treasure hunt with their crew. "Alright, me hearties! I shall share the gems and gold equally with you all and any left over is mine!" "Is mine!" Let's help share the treasure equally by learning about division with remainders, area models. Mr. Squeaks has fifty-nine gems to be shared between five crew mates! When using division to find remainders, we can use area models like this. Split the area model into columns to match the number of place values in the dividend. Fifty-nine has two place values, tens and ones, so split the area model into two columns. Then, write the divisor, five, on the left side of the area model. Next, write fifty-nine here. Now think, what number, when multiplied by five, has a product that is close to, but doesn't go over, fifty-nine? It is often easier to multiply by tens first when dividing two-digit numbers with area models. So write ten above the column. Then, multiply the divisor, five, by ten to get the product, fifty. Now, subtract fifty from fifty-nine to get nine, and carry it over to the next column. Now we need to identify how many times five, goes into the leftover value, nine. Five goes into nine only one time, so write one here. Now, multiply five by one, to get five. Then, subtract five from nine to get four. Since five cannot go into four, we add the numbers above the columns to find the quotient. Ten plus one equals eleven. Since there are four leftover, this is the remainder. Write an R to represent remainder, followed by four. Fifty-nine divided by five equals eleven with four remaining meaning the five crew mates will get eleven gems each, with four left for Mr. Squeaks. Now, Mr. Squeaks wants to share three hundred forty-seven coins between three crew mates! What is the first step? Split the area model into three columns, since the dividend has three place values, hundreds, tens, and ones. What happens with the divisor and dividend? Write the divisor, three, on the left side of the area model, and write the dividend inside the first column. Now find a three-digit number, when multiplied by three, has a product that is close to three hundred forty-seven. It is often easier to multiply by hundreds and tens first when dividing three-digit numbers with area models. What could we multiply three by? We could multiply three by one hundred, so write it here. Three times one hundred is three hundred, so subtract three hundred from three hundred forty-seven to get forty-seven. What is the next step? Write forty-seven here. What number, when multiplied by three, has a product close to forty-seven? We could multiply three by ten, so write it here. Three times ten is thirty so subtract thirty from forty-seven to get seventeen. What is the next step? Write seventeen here. What number, when multiplied by three, has a product that is close to seventeen? Five, so write five here. Three times five is fifteen, so subtract fifteen from seventeen, which is two. What is the final step? Add all the numbers above the columns to get one hundred fifteen. Don't forget to represent the remainder by writing R two. Three hundred forty-seven divided by three equals one hundred fifteen with two remaining, meaning the three crew mates will get one hundred fifteen coins each, with two remaining for Mr. Squeaks. While Mr. Squeaks finishes up, let's review! Remember, when dividing using area models first, divide the area model to match the number of place values in the dividend. Second, write the divisor on the left side. Third, find a multiple of the divisor that is close to, but doesn't go over, the dividend. Fourth, subtract the product from the dividend and carry the leftover to the next column. Repeat steps three and four until you are left with a remainder. Add the numbers above the columns for the quotient, then write R followed by the remainder. "Captain Squeaks, what about our treasure!?"
Division with Remainders (Area Models) exercise
-
How do we solve division problems using an area model?
HintsOnce you have the area model drawn with the divisor on the left hand side, what do you do with the dividend?
Look at this area model to help you to see the steps. So far, we have found a first multiple of the divisor and subtracted this from the total. What do we do next?
How do we find our final answer?
Solution- First, divide the area model to match the number of place values in the dividend.
- Next, write the divisor on the left side.
- Then, find a multiple of the divisor that is close to, but doesn't go over, the dividend.
- Now, subtract the product from the dividend and carry the leftover to the next column.
- Repeat steps three and four until you are left with a remainder.
- Add the numbers above the columns for the quotient, then write R followed by the remainder.
-
Can you help Mr. Squeaks divide the gems?
HintsWhat would be a good multiple of 6 to start with? Write this at the top left of box.
We can multiply 6 by 10 to get 60 and then subtract this from 81.
What is a multiple of 6 that is close to 21?
SolutionThe correct answer is 13 R3.
The crew mates would get 13 gems each and there would be 3 remaining for Mr. Squeaks.
-
Has Mr. Squeaks solved this problem correctly?
HintsHas the area model been set up correctly? Is the divisor on the left hand side?
What has each number been multiplied by? This is the number that should be at the top of each column.
4 x 50 = 200. Does this help you to check the first column?
Have the numbers at the top been added correctly to find the answer?
Try solving 267 $\div$ 4 yourself with your own area model and then seeing what is different.
SolutionHere we can see the correct area model and answer.
- 4 x 50 = 200. The number above the first column should be 50, not 40.
- 4 x 10 = 40. The number above the second column should be 10, not 4.
- 4 x 6 = 24. The number above the third column should be 6, not 8.
- 50 + 10 + 6 = 66. When we add the correct numbers together we get 66, not 53.
-
Can you match the problems to the answers?
HintsTo draw your own area model, first divide it into the correct number of boxes to match the number of place values in the number being divided.
To solve 96 $\div$ 7, we could start an area model like this. What have we multiplied 7 by to make 70?
7 x 10 = 70 so we write 10 at the top of the left column. 96 - 70 = 26 so we carry this to the right side. What has 7 been multiplied by to make 21?
Once you have completed the columns in your area model, add the numbers at the top and then write your remainder.
SolutionHere we can see an area model used to solve 96 $\div$ 7.
- First we draw our area model with two columns as 96 has two place values.
- We then put 7 on the left hand side.
- 7 x 10 = 70 so we write 10 at the top of the left column and subtract 70 from 96 to get 26.
- 7 x 3 = 21 so we write 3 at the top of the right column and subtract 21 from 26 which equals 5.
- 7 does not go into 5 so this is our remainder.
- 10 + 3 = 13 therefore 96 $\div$ 7 = 13 R 5
- 111 $\div$ 8 = 13 R 7
- 176 $\div$ 3 = 58 R 2
- 241 $\div$ 4 = 60 R 1
-
Can you share the coins?
HintsWhich number in the equation is the divisor? Remember, this needs to go on the left of the model.
If we subtract 50 from 62 we get 12. What do we subtract from 12 to get 2?
We now need to figure out which number we add to 10 to make 12.
Solution62 $\div$ 5 = 12 R 2
- First of all, we need to add the divisor, 5 to the left of the model.
- In the left hand column, we have multiplied 5 by 10 to get 50. This is then subtracted from 62 to give us 12.
- We can then add 12 to the top of the right column. What is a multiple of 5 that is near 12? 10. 12 - 10 = 2.
- We multiplied 5 by 2 to get 10 so 2 is placed above the right column.
- We can then see from the right column that we are left with a remainder of 2 so we add this to the answer at the top.
-
The Treasure Chest.
HintsRemember, you can get a pencil and paper and draw your own area models to help you to solve each problem.
Think about how many place values the dividend has and how many columns your area model will need.
You could multiply your divisor by 50 the first time. How many would this leave you with?
For example, if we are solving 479 $\div$ 6, we could multiply 6 by 50 to get 300 then subtract this from 479 before carrying on with our next steps.
SolutionThere were 479 coins which Mr. Squeaks wanted to share between 6 crew mates. Each crew mate got 79 coins and there was a remainder of 5 for Mr. Squeaks. (Above you can see an example area model solving this problem.)
There were also 394 diamonds. Each of 7 crew mates got 56 diamonds and Mr. Squeaks took the remainder of 2.
Finally they found 247 rubies. These were shared between 4 crew mates who each got 61. This left Mr. Squeaks with a remainder of 3.


















