Word Problems with Quadratic Equations

Basics on the topic Word Problems with Quadratic Equations
There are many ways to solve quadratic equations. You can factor them, complete the square, graph them, and use the quadratic formula, for instance.
At least one of these methods can be used to solve any problem involving a quadratic equation, and which method you choose depends on the kind of problem you are presented with.
If the quadratic equation can be represented by mapping or a table, then graphing can do the trick. If the quadratic equation is factorable, then factoring, of course, and completing the square are good choices. When the quadratic equation has coefficients that are real numbers, like decimals, fractions, or maybe even radicals, then using the quadratic formula is highly recommended.
One must note though that these problems often look for concrete answers, like units of measurement or quantity. A negative root, though a valid solution to a quadratic equation, may not be the answer that a word problem is looking for. A positive root, or possibly roots, then is the more appropriate final answer.
Analyze Functions Using Different Representations.
CCSS.MATH.CONTENT.HSF.IF.C.8.A
Transcript Word Problems with Quadratic Equations
The mighty King Wallace sits on his throne and rules his kingdom every day of the year, except for his birthday. Every year, to celebrate his birthday he takes a trip to visit various scenic outlooks and famous locations within his kingdom. For this year’s birthday celebration, the decision is difficult, there're so many destinations to choose from.But finally, the mighty king decides to visit one of the more beautiful castles in his kingdom for the umteenth time. To prepare for the king's visit, the servants must cover the ground around the castle with carpet, so the King’s shoes won’t get dirty. How much carpet do they need?
Setting up the quadratic equation
To figure this out, we can use a quadratic equation. Take a look at the diagram of the castle. The length of the area that needs carpet is equal to an unknown length, 'x', plus 9, the width is 'x' + 3, and the total area is 72 square wallacesons. You might be wondering, what’s a wallaceson? King Wallace devised his very own system of weights and measures. I know! What a narcissist but whatever, right?! Okay back to the problem. To help the servants figure out the amount of carpet they need, we can set up an equation and solve for 'x'. First use FOIL: first, outer, inner, last. You know the drill.
Factoring the quadratic equation
Next, you'll need to factor the quadratic equation. Using the standard form of the quadratic equation as your guide, set the equation equal to zero. Then find the product of ac that sums to 'b'. That's negative 3 and 15. Now set each of the two binomials factors equal to 0. You're not done yet; you still have to solve for 'x'. Use opposite operations to solve each mini equation. X has two possible solutions, 3 and negative 15.
Completing the square
But factoring’s not the only game in town. We can also solve for 'x' by completing the square. FOIL first, so it's easier to work with. To complete the square, follow these steps: Move the constant to the other side of the equal sign. Then take the 'b' value, divide it by 2, and square it, and then add this number to both sides of the equation. Factor the left side of the equal sign and finally, solve for 'x', by taking the square root of each side of the equal sign and finish it off with PEMDAS. X is equal to 3 and -15, just like before.
Let’s plug in the values for 'x' into the equation, so the servants can order the carpet. Plug in 'x' is equal to 3. The measurements are 12 wallacesons by 6 wallacesons! That’s a big carpet! Now for the second value, 'x' = -15. The measurements of the carpet are equal to -6 and -12. You can’t have a negative measure of carpet so although 'x' = -15 works as a solution for the quadratic equation. It’s not a valid solution for this situation. So the correct solution is 'x' is equal to 3.
Indecisive as always, the king changes his mind at the very last minute and decides he wants to visit a place he’s never been to before. He'll go to a village near the border of his kingdom. He’s been curious about this village because he heard they have some unusual customs. When the King gets to the village, the villagers seem normal enough. The villagers stand with baskets of apples patiently waiting for his speech to begin. Luckily for the king, his squire knows all about the village's unusual customs, the villagers always give an enthusiastic welcome to visitors. By throwing apples at them! To keep the king safe, the squire will have to control the crowd, but how can he do that?
Graphing the parabola
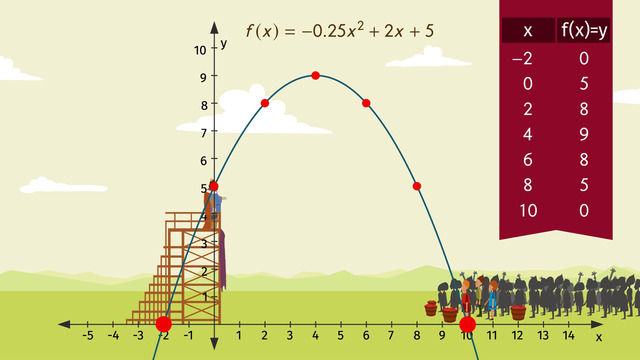
The king will give his speech while standing on a tower 5 wallace yards high, at the point on the graph (0, 5). The trajectory of the apples can be described by the function of 'x' = -0.25x² + 2x + 5, since it's a quadratic equation, we know the shape of the graph is a parabola. So, where does the crowd need to stand to so they won't be able to hit the king with apples? This whole situation sounds a little crazy, right? What can you do? You have to respect peoples' customs, right?
Let’s solve this problem by graphing. Plug in a few points for 'x' and determine the corresponding 'y' values. Plot the points and then draw in the parabola. Where the graph touches the x-axis is a possible solution set for this quadratic equation, at 'x' = 10 and -2. The king will be safe as long as the crowd is placed more than 10 feet in front of the podium or 2 feet behind.
Quadratic formula
We can also calculate the solution by using the quadratic formula. Use the standard quadratic equation as your guide to determine the values for a, b, and c, but first manipulate the equation so the 'a' value is equal to positive 1. You could skip this step, but it makes the numbers easier to work with. Now substitute the 'a', 'b' and 'c' values into the quadratic formula, and then do the math. The answer is the same as before, 'x' is equal to 10 and -2. Just as the squire expected, the crowd welcomed the king by throwing lots of apples but thanks to the quadratic equation, the king gave his speech without a single apple finding its mark.
Word Problems with Quadratic Equations exercise
-
Explain how to solve a quadratic equation by factoring.
HintsThe FOIL method a way of multiplying two binomials together. For example, $(x+9)(x+3)$:
- multiply the First $x^2$
- multiply the Outer $9x$
- multiply the Inner $3x$
- multiply the Lasr $27$
Here is an example for solving an equation; subtraction is the opposite operation of addition.
Use the zero factor property: if a product is equal to zero then one of its factors must also be equal to zero.
SolutionThe servants have to calculate the total length of the carpet.
To do this they first use the FOIL method for multiplying the two binomials:
$(x+9)(x+3)=x^2+9x+3x+27=x^2+12x+27$
This quadratic term is equal to the given total area. So we get
$x^2+12x+27=72$
which is equivalent to
$\begin{array}{rcl} x^2+12x+27&=&~72\\ \color{#669900}{-72} & &\color{#669900}{-72}\\ x^2+12x-45&=&~0. \end{array}$
To factor the left-hand side of the equation above we are looking for pairs of factors of $-45$ which sum to $12$:
- $1\times(-45)=-45$ but $1-45=-44$
- ...
- $3\times (-15)=-45$ but $3-15=-12$
- $-3\times 15=-45$ and $-3+15=12$ $~~~~~$✓
To get the solutions we use opposite operations twice:
$\begin{array}{rcl} x-3&=&~0\\ \color{#669900}{+3} & &\color{#669900}{+3}\\ x&=&~3 \end{array}$
and
$\begin{array}{rcl} x+15&=&~0\\ \color{#669900}{-15} & &\color{#669900}{-15}\\ x&=&~-15 \end{array}$
For $x=3$ we get that the length is $3+9=12$ and the width is $3+3=6$. And for $x=-15$, the length is $-15+9=-6$ ... so we can stop because there don't exist any negative lengths.
This means that both $x=3$ as well as $x=-15$ are solutions to the quadratic equation, but only $x=3$ is a possible solution in our given situation.
-
Determine how to solve quadratic equations graphically.
HintsThe function above is a quadratic function.
Any linear function is given by $f(x)=mx+b$, where $m$ is the slope and $b$ the $y$-intercept. The graph of such a function is a line.
The graph of a quadratic function is a parabola. Each parabola has at most two $x$-intercepts.
SolutionThere exist different ways to solve quadratic equations like $ax^2+bx+c=0$.
For example, lets draw the parabola in a coordinate plane which corresponds to the graph of
$f(x)=-0.25x^2+2x+5$
- Plug in a few values for $x$ and calculate the corresponding $y$-values.
- Plot the resulting ordered pairs $(x,y)$ in a coordinate plane.
- Connect those pairs to get the corresponding parabola.
-
Determine how to solve quadratic equations by completing the square.
HintsThe FOIL method is a way of multiplying two binomials; for example, $(x+2)(x-3)$:
- multiply the First $x^2$
- multiply the Outer $-3x$
- multiply the Inner $2x$
- multiply the Lasr $-6$
To complete a quadratic term $x^2+bx$ add $\left(\frac b2\right)^2$.
Here is an example for solving an equation by taking a square root.
Don't forget the $\pm$ sign in your calculation!
Check the solutions. Do they makes sense when trying to determine the positive length and width of the moat?
SolutionFirst, we use the FOIL method for multiplying the two binomials
$(x+2)(x-3)=x^2-3x+2x-6=x^2-x-6$
This must be equal to the given total area. So we get $x^2-x-6=50$, which is equivalent to
$\begin{array}{rcl} x^2-x-6&=&~50\\ \color{#669900}{+6} & &\color{#669900}{+6}\\ x^2-x&=&~56 \end{array}$
Now we complete the quadratic term on the left-hand side to a square. For this we add $(\frac12)^2$:
$\begin{array}{rcl} x^2-x&=&~56\\ \color{#669900}{+\left(\frac12\right)^2} & &\color{#669900}{+\left(\frac12\right)^2}\\ x^2-x+\left(\frac12\right)^2&=&~56+\left(\frac12\right)^2\\ \left(x-\frac12\right)^2&=&~56.25 \end{array}$
Next, we take the square root of both sides to get
$x-\frac12=\pm7.5$
Lastly we add $\frac12=0.5$, which leads to the desired solutions
$x=0.5+7.5=8$ or $x=0.5-7.5=-7$
Let's check if both solutions work with the problem at hand, keeping in mind that we are trying to find the length and width of a moat.
For $x=8$ we get the length $8+2=10$ and the width $8-3=5$. Both are positive, so this solution works.
For $x=-7$ we get the length $-7+2=-5$ and the width $-7-3=-10$. A negative length and width doesn't make any sense, so this solution can't work in our given situation.
-
Calculate where the castle ditches have to be built by using the quadratic formula.
HintsYou can use the quadratic formula with
- $a=-0.5$
- $b=-1.5$
- $c=5$
You can also multiply the equation $-0.5x^2-1.5x+5=0$ by $-2$ to get $x^2+3x-10=0$.
Both solutions are whole numbers. One is negative and the other one is positive.
SolutionYou can solve each quadratic equation $ax^2+bx+c=0$ by using the quadratic formula,
$x=\frac{-b \pm\sqrt{b^2-4ac}}{2a}$.
First, determine $a$, $b$ and $c$ in the equation and then plug those values into the quadratic formula.
For $-0.5x^2-1.5x+5=0$, we have that $a=-0.5$, $b=-1.5$, and $c=5$.
So we calculate
$\begin{array}{rcl} x&=&\frac{1.5\pm\sqrt{(-1.5)^2-4(-0.5)(5)}}{2(-0.5)}\\ &=&~\frac{1.5\pm\sqrt{2.25+10}}{-1}\\ &=&~-1.5\pm\sqrt{12.25}\\ x_1&=&~-1.5+3.5=2\\ x_2&=&~-1.5-3.5=-5 \end{array}$
The desired solutions are then $x=2$ or $x=-5$.
Perhaps you'd like to multiply the quadratic equation $-0.5x^2-1.5x+5=0$ with $-2$ to get $x^2+3x-10=0$. You don't have to do it but it makes the calculations a little bit less complicated.
-
Name the methods for solving quadratic equations.
HintsThe solutions of the corresponding quadratic equation are $x=10$ and $x=90$.
This is the quadratic formula.
The zero factor property states that if a product is equal to zero, then one of its factors must also equal zero.
It doesn't matter at all which method you choose to find the solutions. If the solutions exist, then they are always the same.
SolutionIf you have to solve a quadratic equation like $ax^2+bx+c=0$, or with $a=1$, $x^2+bx+c=0$, which you can derive by dividing the equation $ax^2+bx+c=0$ by $a$, then you can decide from several methods:
- You could factor the left-hand side of the equation $x^2+bx+c=0$ to $(x+d)(x+e)=0$ and get the solutions $x=-d$ and $x=-e$.
- You can complete the square to get $(x+e)^2=d$. You can solve this equation by taking the square root of both sides.
- You can use the quadratic formula for solving $ax^2+bx+c=0$.
- You also could draw the parabola corresponding to $f(x)=ax^2+bx+c$. The $x$-intercepts of this parabola are the desired solutions.
-
Solve the following quadratic equations.
HintsDecide which method you you like to use. No matter which method you choose, your results will always be the same.
Here you see the quadratic formula for solving quadratic equations like $ax^2+bx+c=0$.
For solving a quadratic equation $x^2+bx+c=0$ by factoring, find the factors of $c$ which sum to $b$.
Here is an example of complete the square of a quadratic equation.
SolutionLet's solve the various quadratic equations using the different methods we learned:
First, lets use the method of factoring for the quadratic equation $x^2-2x-8=0$:
- Look for the factors of $8$ which sum to $-2$, namely $2\times (-4)=-8$ and $2-4=-2$ $~~~~~$✓.
- Thus we get the equivalent equation $(x+2)(x-4)=0$ which we solve by using opposite operations:
$\begin{array}{rcl} x+2&=&~0\\ \color{#669900}{-2} & &\color{#669900}{-2}\\ x&=&~-2 \end{array}$
or
$\begin{array}{rcl} x-4&=&~0\\ \color{#669900}{+4} & &\color{#669900}{+4}\\ x&=&~4 \end{array}$
This method (better!) works for whole solutions.
$~$
Next, let's solve $x^2-8x+7=0$ by completing the square:
- Subtract $7$ from both sides to get $x^2-8x=-7$.
- Adding $4^2$ on both sides leads to $x^2-8x+4^2=-7+4^2$.
- $(x-4)^2=9$ is the resulting equation.
- Take the square root on both sides and don't forget the $\pm$ sign: $x-4=\pm3$.
- Almost done: add $4$ to get $x=4+3=7$ or $x=4-3=1$.
You can also use the quadratic formula, which we will use to solve $2x^2+4x-6=0$. Nothing that $a=2$, $b=4$, and $c=-6$, we have that
$\begin{array}{rcl} x&=&~\frac{-4\pm\sqrt{(-4)^2-4(2)(-6)}}{2(2)}\\ &=&~\frac{-4\pm\sqrt{16+48}}{4}\\ &=&~\frac{-4\pm\sqrt{64}}{4}\\ x_1&=&~\frac{-4+8}{4}=1\\ x_2&=&~\frac{-4-8}{4}=-3 \end{array}$
$~$
For $0.2x^2+1.2x+1=0$, first multiply both sides of the equation by $5$ to get $x^2+6x+5=0$, and thus $a=1$, $b=6$ and $c=5$. This simplifies the following calculation:
$\begin{array}{rcl} x&=&~\frac{-6\pm\sqrt{6^2-4(1)(5)}}{2(1)}\\ &=&~\frac{-6\pm\sqrt{36-20}}{2}\\ &=&~\frac{-6\pm\sqrt{16}}{2}\\ x_1&=&~\frac{-6+4}{2}=-1\\ x_2&=&~\frac{-6-4}{2}=-5 \end{array}$
What are Quadratic Functions?
Graphing Quadratic Functions
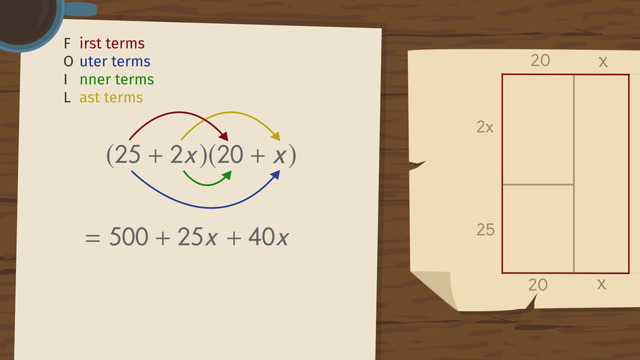
FOILing and Explanation for FOIL

Solving Quadratic Equations by Taking Square Roots
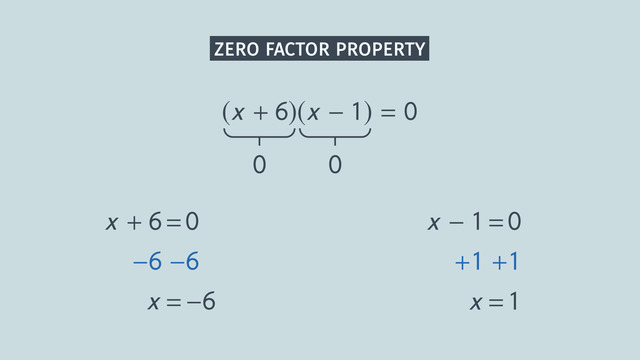
Solving Quadratic Equations by Factoring
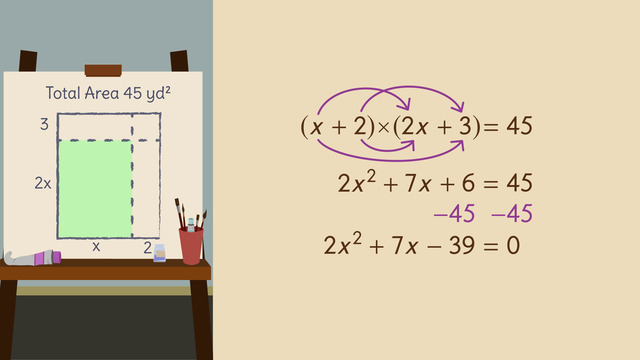
Factoring with Grouping

Solving Quadratic Equations Using the Quadratic Formula

Solving Quadratic Equations by Completing the Square
Finding the Value that Completes the Square
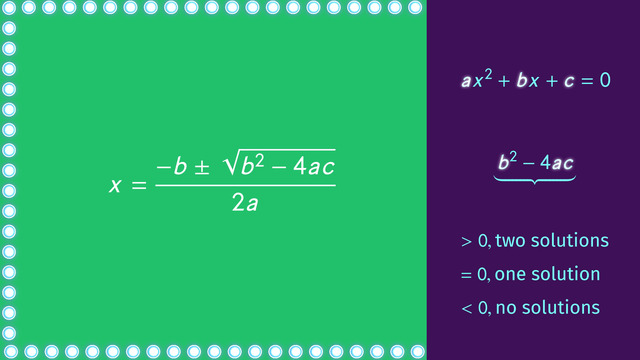
Using and Understanding the Discriminant

Word Problems with Quadratic Equations











