What are Quadratic Functions?
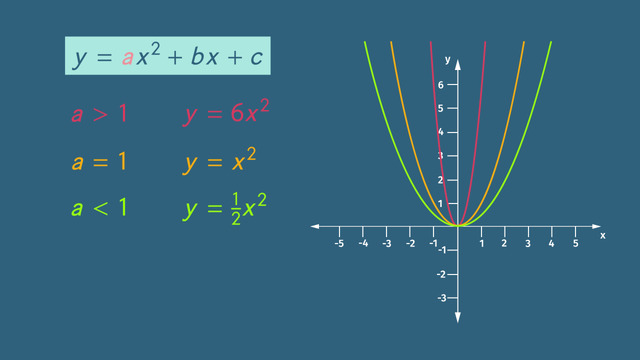

Basics on the topic What are Quadratic Functions?
Summary of What are Quadratic Functions
A quadratic function is represented by the standard form, y = ax2 + bx + c.
In order for such an equation to be a quadratic function, and not a linear one, we must have that the coefficient a is not equal to zero; i.e. a ≠ 0.
The graph of a quadratic function is a parabola. The larger the absolute value of a is, the thinner the shape of the parabola becomes. The smaller the absolute value, the wider the parabola becomes.
The coefficient a is also an indicator of the direction of the shape of the parabola. If the value of a is positive, the parabola opens upwards. If the value of a is negative, the parabola opens downwards.
Graph linear and quadratic functions and show intercepts, maxima and minima.
Common Core Reference
CCSS.MATH.CONTENT.HSF.IF.C.7.A
Let's practice: quadratic functions Exercises
With the following exercises on the topic of quadratic functions, you can test whether you have understood everything. Test your knowledge now!
Transcript What are Quadratic Functions?
"You've seen the posters. You've seen the billboards. Now drink the drink. The question of the summer is about to be answered. The Quadratic Functions are proud to present a refreshing line of new drinks, Parabolica! Parabolica XTRA Strong is just amazing. It makes gravity work better!"
”That jump is a perfectly shaped parabola! What a gorgeous u-shape! You'll love the extra strong flavor. It’s simply refreshing. You wanna know Parabolica's secret ingredients? We're gonna tell ya. PARABOLAS! You may be wondering, is there a standard form like with linear functions? You betcha!”
A quadratic equation, written in standard form, is equal to y=ax²+bx+c for all 'a's not equal to zero.
”Wanna be a quadratic function, too? Then the 2nd degree is the way to be! Tame your inner beast, just look at that beautiful parabola! Also from quadratic functions: Parabolica Chill! Try it! Feel the thrill of Parabolica Chill! This drink will give you energy, but not quite so much."
Back to parabolas and quadratic equations. Let's investigate some characteristics of the equations and their corresponding graphs. The 'a' value, the coefficient of the squared variable, determines the width of the parabola. The greater the 'absolute' value of a, the thinner the parabola. This is the graph of the quadratic equation, with 'a' = 1: y = x². And this is a graph of a quadratic equation, with 'a' less than 1: y = (1/2)x². And here we have 'a' greater than 1: y = 6x². When we compare to the graph of y = x², it's almost as if were on a diet...
Ok, enough math, back to the energy drinks.
_”Something weighing you down? Try the new Parabolica Lite – you’ll feel light as a feather!
You might even defy gravity!”
”Will you just take a look at that nicely-shaped parabola?! See how light he is after drinking Parabolica Lite? Wanna know another secret about Parabolas?”
The sign of the 'a' value affects a parabola's direction. When the 'a' value is negative, the parabola is shaped like a frown. But when the 'a' value is positive, we can turn that frown upside down!
”Now that we've told you all the secret ingredients for Parabolas" Oh dear! It seems they should have invested more money in getting just the right taste - rather than on special effects
What are Quadratic Functions? exercise
-
Decide if the given shape is a parabola.
HintsA parabola looks like a rainbow or a smile.
A parabola doesn't have an angle.
Three of the given examples are parabolas.
SolutionA parabola is shaped like a rainbow.
The standard form of an equation for a parabola is given by
$y=ax^2+bx+c$.
Depending on the sign of $a$ you can determine the direction of the parabola; the parabola can look like a rainbow itself or smile.
There are three images showing a parabola:
- The plane flying.
- The dolphin jumping.
- The swimmer jumping.
-
Describe a quadratic function and the role of $a$.
HintsAn example:
$y=3x^2-2$ is an example of a quadratic function.
SolutionA quadratic function in standard form is given by
$y=ax^2+bx+c$.
Depending on $a$ you can decide the width of the parabola.
For example, let's see when the parabola $y=ax^2$ is thinner than $y=x^2$, and when $y=ax^2$ is wider than $y=x^2$.
The greater the absolute value of $a$, the thinner the parabola.
So when $a>1$, the parabola $y=ax^2$ is thinner than $y=x^2$.
And when $0<a<1$, the parabola $y=ax^2$ is wider than $y=x^2$.
-
Identify the value of the coefficient $a$ of each parabola.
HintsThe greater the absolute value of $a$, the thinner the parabola.
One of the parabolas is the graph of $y=x^2$.
Each quadratic function has the form $y=ax^2$, with $b=c=0$.
Check the $(x,y)$ pairs lying on the parabola.
SolutionThe parabola to the right is the graph of $y=x^2$. So $a=1$.
How can this be determined? Look at some $(x,y)$ points lying on the parabola: $(1,1)$, $(2,4)$, $(-1,1)$. All these points satisfy $y=x^2$.
The smallest $a$ is given by $a=\frac14$. The parabola corresponding to $y=\frac14x^2$ could be determined by the points $(2,1)$ and $(4,4)$.
Next we have $a=\frac12$, which can be determined via the points $(2,2)$ and $(1,0.5)$.
Then we have $a=1$, which is pictured here to the right.
Then we have the parabola which is the graph of $y=1.5x^2$; so $a=1.5$. This can be detected by the points $(1,1.5)$ or $(2,6)$.
The last parabola corresponds to $y=3x^2$; $a=3$ and $(1,3)$ satisfies $y=3x^2$.
-
Find the corresponding quadratic function.
HintsEach quadratic function has the form $y=ax^2$.
Keep the following in mind:
- If $a>0$, then the parabola looks like a rainbow.
- If $a<0$, then the parabola looks like a smile.
Each pair $(x,y)$ on a parabola must satisfy $y=ax^2$.
SolutionEach of the parabolas above belongs to a quadratic function of the form $y=ax^2$.
First we look at the sign of $a$: the yellow as well as the red parabola are opened downwards, or are "rainbow shaped". The blue and the green parabola are opened upwards, or are "smile shaped".
Next we pick some points $(x,y)$ lying on each parabola:
- For the blue parabola, we pick the point $(3,3)$, and check: $y=\frac13 3^2=\frac93=3$. ✓
- For the green parabola, we pick the point $(1,2)$ and check: $y=2\times1^2=2\times 1=2$. ✓
- For the red parabola, we pick the point $(1,-1)$ and check: $y=-1^2=-1$. ✓
- For the yellow parabola, we pick the point $(-3,-3)$ and check: $y=-\frac13\times(-3)^2=-\frac93=-3$. ✓
-
Determine which functions are quadratic functions.
HintsA quadratic function means that the hightest power is $2$.
For example, $y=mx+b$ is a linear function, where the highest power $1$.
The following is an example of a quadratic function:
$y=\frac12x^2+x$.
SolutionThe standard form of a quadratic function is given by
$y=ax^2+bx+c$.
So the highest power is $2$ and $a\neq 0$. Otherwise we would have a linear function $y=mx+n$.
With $a=1$ and $b=c=0$, the function $y=x^2$ is quadratic, as well as the functions:
- $y=6x^2$ with $a=6$ and $b=c=0$.
- $y=\frac12 x^2$ with $a=\frac12$ and $b=c=0$.
-
Explain how to find the corresponding quadratic function.
HintsThe standard form of a quadratic function is given by
$y=ax^2+bx+c$.
The sign of $a$ determines if the corresponding parabola is opened upwards or downwards.
The larger the absolute value of $a$, the thinner the parabola. Similarly, the smaller the absolute value of $a$, the wider the parabola.
SolutionHere you see a parabola, the graph of a quadratic function.
How can you determine the corresponding equation?
- Keep the standard form in mind: $y=ax^2+bx+c$.
- The vertex of the parabola is the origin, so we have $b=c=0$ and thus that our equation is of the form $y=ax^2$.
- The parabola is opened upwards. Thus we know that $a$ must be positive.
- The parabola is thinner than the parabola corresponding to $y=x^2$ (i.e. the red parabola in the picture to the right). You can recognize this, for example, by looking at the point $(1,1)$ on $y=x^2$, and $(1,2)$ on the blue parabola in question. Thus $a$ must be greater than $1$.
- To determine $a$, plug a point on the parabola into $y=ax^2$. For example, the point $(2,8)$ gives us $8=a\times 2^2$. Dividing by $4$ results in $a=2$.
What are Quadratic Functions?
Graphing Quadratic Functions
FOILing and Explanation for FOIL

Solving Quadratic Equations by Taking Square Roots
Solving Quadratic Equations by Factoring
Factoring with Grouping

Solving Quadratic Equations Using the Quadratic Formula

Solving Quadratic Equations by Completing the Square
Finding the Value that Completes the Square
Using and Understanding the Discriminant
Word Problems with Quadratic Equations









