The Pythagorean Theorem
- What is the Pythagorean Theorem?
- Understanding the Pythagorean Theorem
- Brief History
- Real-World Examples


Basics on the topic The Pythagorean Theorem
What is the Pythagorean Theorem?
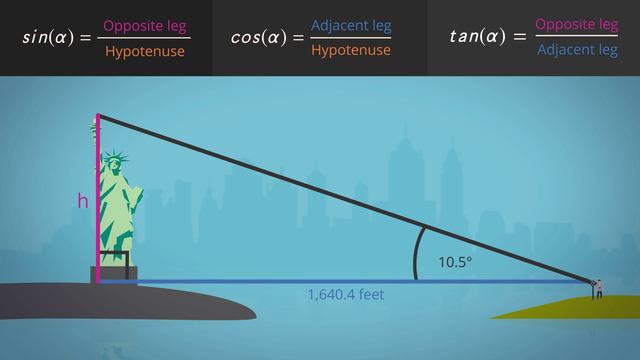
The Pythagorean Theorem is a practical and essential concept in geometry, widely used in numerous real-world scenarios. From determining the shortest path in navigation to calculating the height of a building or the length of a ramp, this theorem is a fundamental tool. It's not just a mathematical formula; it's a practical solution for various everyday problems involving right triangles.
Understanding the Pythagorean Theorem
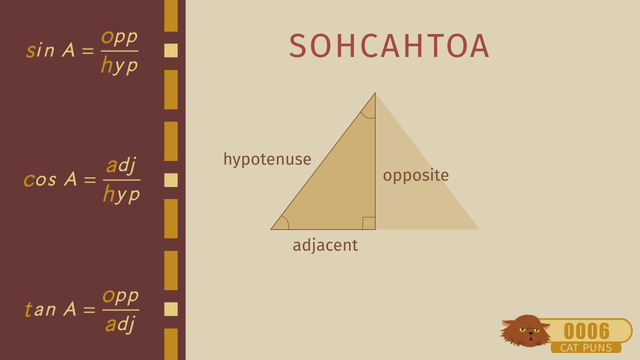
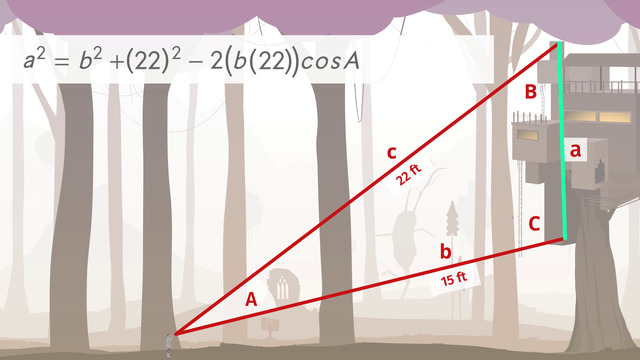
The Pythagorean Theorem states that in a right triangle, the square of the hypotenuse (the side opposite the right angle) equals the sum of the squares of the other two sides, known as the legs. The theorem is typically written as a2+b2=c2 where the c is the hypotenuse, or the longest side, and the a and b are the legs of the triangle.
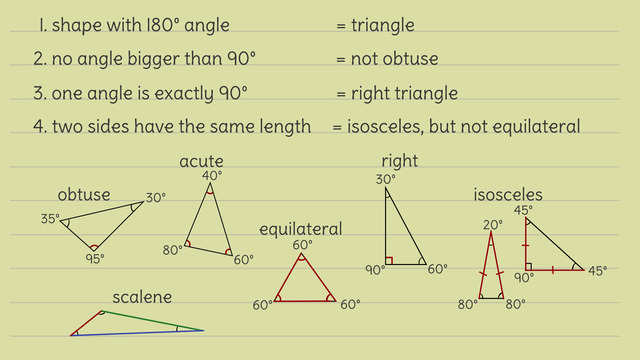
The Pythagorean equation specifically works for a right triangle, but to learn more about other triangles, check out this video: Classifying Triangles by Angles
Brief History
The theorem is named after the Greek mathematician Pythagoras, who popularized it, though it was known in various cultures before his time.
Real-World Examples
The Pythagorean Theorem is widely used in the real world. Here we provide some examples from the fields of architecture, navigation and technology:
| Application Area | Use of Pythagorean Theorem |
|---|---|
| Architecture and Construction | Calculating the height of a structure or the length of a supporting beam. |
| Navigation | Determining the shortest path between two points. |
| Technology | Designing components in various fields of engineering. |
Using the Theorem – Step-by-Step Examples
Identify the Right Triangle: First, ensure you're working with a right triangle (one angle is 90 degrees).
Label the Sides: Label the longest side (opposite the right angle) as c (the hypotenuse). The other two sides are labeled a and b and are called the legs.
Apply the Formula: Use a2 + b2 = c2 to find the missing side. If you know c and one leg, solve the formula to find the other leg. Solve the equation for the missing variable, and if you need a recap on solving equations this video will help: Solving One-Step Equations.
Let’s go through this exercise together!
If a ladder is placed against a wall and reaches $15$ feet high, and the base is $9$ feet away from the wall, how long is the ladder?
- Firstly, label your hypotenuse $c$, and the legs $a$ and $b$.
- Next, substitute the known values into the theorem 92 + 152 = c2.
- Then, calculate: 81 + 225 = c2.
- Finally, solve for $c$: $c = \sqrt{306} \approx 17.5$ feet.
Let’s complete one more exercise together.
A rectangular park measures 80 meters by 60 meters. Find the length of the diagonal path across the park.
Notice this rectangle is made up of two right triangles if we draw a diagonal line connecting one corner to the other. These right triangles are identical but just flipped.
- First, label your sides $a$, $b$, and $c$.
- Next, substitute the known values into the theorem: 802 + 602 = c2.
- Then, calculate: 6400 + 3600 = c2.
- Finally, solve for $c$: $c = \sqrt{6400 + 3600} = \sqrt{10000} = 100$ meters.
The Pythagorean Theorem – Exercises with Solutions
The Pythagorean Theorem – Summary
- At its core, the Pythagorean Theorem provides a mathematical method to determine the relationship between all three sides of any right-angled triangle.
- The Pythagorean Theorem, crucial for calculations in right triangles, asserts that a2 + b2 = c2, where $c$ is the hypotenuse and $a$ and $b$ are the other two sides.
- Applied in diverse real-world situations such as architecture, navigation, and technology, this theorem helps calculate distances and structural dimensions.
- To solve for an unknown side, square the lengths of the known sides, add or subtract these values, and take the square root of the result to find the missing measurement.
- Pythagorean triples, like $(3, 4, 5)$ or $(5, 12, 13)$, provide quick reference solutions for some commonly encountered right triangles.
Discover more about geometry with our interactive practice problems, videos, and worksheets on our platform!
For more practice applying the Pythagorean Theorem, check out this video: Applying the Pythagorean Theorem.
Frequently Asked Questions – The Pythagorean Theorem
Transcript The Pythagorean Theorem
Damo, the son of Pythagoras, wants to build a vacation cottage for his mother and father. In keeping with the family business of triangles, Damo decides to incorporate the shape into the design of the cottage. What a perfect time to use his dad's theorem:The Pythagorean Theorem!
Right Triangles and Pythagorean Triples
For the roof of the cottage, Damo will use a triangle design, but what size and shape should the triangle be? Damo's dad spoke of many combinations of integers to create the three sides of right triangles, called Pythagorean triples, but which one is best? Damo thinks back to his dad's class on triangles from school. His dad taught him well! He remembers that right triangles have one and only one right angle, and a right angle is equal to 90°. Even though one angle has to be 90°, there are several different combinations of side lengths that Damo can use.
These special relationships are called Pythagorean Triples. If the integer side lengths of a triangle create a Pythagorean triple, the formula a² + b² = c² will work. How about this triangle, is it a Pythagorean triple? Let's see. The triangle has a right angle, and if you sum the area of the two smaller squares, the sum is equal to the area of the larger square.
Examples for Pythagorean Triples
Damo has a choice of several different roof shapes, but he wants one in the shape of a right triangle, and it must be just right for the cottage.
The first Pythagorean triple Damo remembers is 3-4-5. Plugging this into dear ol' dad's theorem gives him, 3² + 4² = 5² ...which is 9 + 16 = 25. This is awesome! No wonder dad gets so excited about right triangles. He knows this one is in the shape of a right triangle, but it's too small.
Next, he tries side lengths 8, 15, and 17. Let’s see, is it a right triangle? Shall we try out the theorem? 8² + 15² = 17². So...64 + 225 = 289. Yup, this one works too, but darn – it looks just like the roof on top of Yorgos’ Yogurt Shop, and that just won’t do for his parents.
There are only a few more roof styles that the roof cutters offer: Damo checks the larger roof, with side measures 7-24-25, first. Does it satisfy the theorem? 7² + 24² = 25². This is the same as 49 + 576 = 625. Yes it works, but it’s just too big.
There's one last option, a triangle with side lengths of 5, 12 and 13. I sure hope this one works 25 + 144 = 169. Yeah! This shape is a right triangle, and it's just the right size and style. So Damo picked a roof that's just right. He also practiced the Pythagorean Theorem and learned some Pythagorean triples. Seems like a win, win to me!
The roof of the cottage looks great, and his dad looks very pleased with the shape. Oh no! Damos forgot that different materials have different densities. Oh Geez. Where was Damo when his dad was teaching the unit on density?? I guess he can still learn something from his dear ol' dad. Join us next time for more triangular adventures with Damo!
The Pythagorean Theorem exercise
-
Define the Pythagorean Theorem.
HintsThe Pythagorean theorem focuses on the side lengths of right triangles.
The Pythagorean Theorem focuses on the relationships between the side lengths of right triangles.
Some options in the answer set are true statements about triangles, but are not part of the Pythagorean Theorem.
SolutionThe Pythagorean Theorem relates the side lengths of right triangles. The theorem states that the side lengths of right triangles have a special relationship with each other that is described by the equation $a^2 + b^2 = c^2$. Further, there are sets of integers that satisfy this equation, which are known as "Pythagorean Triples".
Knowing this, let's evaluate each of the statements and determine if they describe the Pythagorean theorem.
- The three side lengths of right triangles form sets called "Pythagorean Triples." ✓ This is correct, and is part of the Pythagorean Theorem.
- A right triangle must have two acute angles. ✗ Although this statement is true, it is not part of the Pythagorean Theorem. This theorem focuses on the side lengths of a right triangle, not the other angles in a right triangle.
- If a triangle is a right triangle, the side lengths $a$, $b$, and $c$, will satisfy the equation $a^2 + b^2 = c^2$. ✓ This is correct, and is part of the Pythagorean Theorem.
- The hypotenuse will always be the longest side of a right triangle. ✗ Although this statement is true, it is not part of the Pythagorean Theorem. It can be proved using the Pythagorean Theorem, though!
-
Determine if the side lengths are a Pythagorean Triple.
HintsRemember that the Pythagorean Theorem can be represented as an equation that uses the squares of the side lengths of a triangle.
The Pythagorean Triples must not include fractions or decimals.
The set of side lengths is a Pythagorean Triple, if they satisfy the equation $a^2 + b^2 = c^2$. This means that the left hand side of the equation must equal the right hand side.
SolutionThe equation given by the Pythagorean Theorem is $a^2 + b^2 = c^2$. Integers that satisfy these equations are known as "Pythagorean Triples".
We are given the side lengths of the triangle: 8, 15, and 17. All being whole numbers, they are definitely also integers. So if the set of numbers satisfies the equation $a^2 + b^2 = c^2$, then it must be a Pythagorean Triple.
The value $c$ is the length of the hypotenuse, which is the longest side. It is also the side across from the right angle. Therefore this side is 17 feet long. Either of the other two sides can act as $a$ or $b$, since they are interchangeable.
Let's assign the values $a = 8$, $b = 15$, and $c = 17$.
Substituting these values in, we get:
$a^2 + b^2 = c^2$
$8^2 + 15^2 = 17^2$
$64 + 225 = 289$
$289 = 289$
The left and right hand sides of the equation are equal. This means that the values satisfy the equation. We can see that this triangle does have side lengths that are a Pythagorean Triple.
-
Find the areas.
HintsHow can you use the Pythagorean Theorem to help you with this question?
The area of each square that is connected to a side represents the literal "square" of that side length. This is equal to the side length, squared.
What is the relationship between the square of each side length?
You can use the equation $a^2 + b^2 = c^2$ to find the area of the square that is attached to the side that has an unknown length.
SolutionIn each of the two cases, we have a right triangle, and we know the lengths of two sides. We must find the area of the square that is connected to the hypotenuse. The area of each square that is connected to a side represents the literal "square" of that side length. This is equal to the side length, squared. We do not know the length of the hypotenuse, but there is another way to find this area.
From the Pythagorean Theorem, we know that:
$a^2 + b^2 = c^2$
We know that $c^2$ represents the area that we must find. We know the side lengths $a$ and $b$.
$a^2 = 3^2$
$a^2 = 9$
$b^2 = 4^2$
$b^2 = 16$
Now we can find $c^2$:
$a^2 + b^2 = c^2$
$9 + 16 = c^2$
$25 = c^2$
Similarly, for the second triangle...
$a^2 = 36$
$b^2 = 64$
$100 = c^2$
-
Decide if the ladder fits.
HintsRemember: the hypotenuse is always the longest side of the a right triangle.
If the equation is satisfied by the given values, then the ladder is the perfect length to fit between the ground and the roof, with the base of the ladder sitting 10 feet from the cottage.
In this question we move straight from the equation $a^2 + b^2 = c^2$, to the square of the values we substitute in. For example, if we had $a = 3$, $b = 4$, and $c = 5$, we would write:
$a^2 + b^2 = c^2$
$9 + 16 = 25$
By doing this, we are skipping the middle step:
$3^2 + 4^2 = 5^2$
SolutionThe ladder, the cottage, and the ground form a right triangle. We are certain about the length of two of the sides of this triangle. We know that the cottage is 24 feet tall. And we know that the bottom of the ladder must sit at least 10 feet from the base of the cottage. The farther away from the cottage the base of the ladder is placed, the longer the ladder will need to be. Let's assume we place the base of the ladder exactly 10 feet from the cottage, so that Damo is able to use the shortest possible ladder.
If the ladder is the correct length, then this set of side lengths should satisfy the Pythagorean theorem, $a^2 + b^2 = c^2$. We know that $c$ should be the hypotenuse. We can see that the ladder, which is 26 feet long, is opposite the right angle. Additionally, the ladder forms the longest side of this right triangle. Therefore it must be the hypotenuse. The other two sides can be labelled $a$ and $b$ interchangably.
$a = 10$
$b = 24$
$c = 26$
By substituting the values in, and simplifying the equation, we can check if the equation is satisfied by these values:
$\begin{array}{rclcl} a^2 + b^2 & = & c^2 &|&\text{subsituting values} \\ 10^2 + 24^2 & = & 26^2 \\ 100 + 576 & = & 676 \\ 676 & = & 676 &|&\text{✓ the two sides are equal} \\ \end{array}$
The two sides of this equation are equal. Therefore the values do satisfy the equation, and the ladder is the correct length.
-
Identify the right triangles.
HintsHow can you determine if a triangle is a right triangle using the Pythagorean Theorem?
What equation can you use to check if a triangle is right, using its side lengths, $a$, $b$, and $c$?
If a triangle's side lengths, $a$, $b$, and $c$, satisfy the equation $a^2 + b^2 = c^2$, then it is a right triangle.
SolutionWe know that if a triangle is right, it's side lengths, $a$, $b$, and $c$, must satisfy the equation:
$a^2 + b^2 = c^2$
We are given the side lengths for each triangle. Let's use the equation to check if the triangles are right angle triangles.
The side lengths of the first triangle are 6, 8, and 10. We know that the value for $c$ must be the longest side of the triangle.
So let's assign the values $a = 6$, $b = 8$, and $c = 10$.
Putting these values into the equation gives us:
$6^2 + 8^2 = 10^2$
$36 + 64 = 100$
$100 = 100$
Since the right hand side is equal to the left hand side, the values of $a$, $b$, and $c$ for this triangle satisfy the equation. That means that this is a right triangle!
Similarly, for the other triangles, we arrive at:
$a = 9$, $b = 40$, $c = 41$:
$81 + 1600 = 1681$ ✓ The left and right sides of this equation are equal, so the triangle is right.
$a = 25$, $b = 60$, $c = 65$:
$625 + 3600 = 4225$ ✓ The left and right sides of this equation are equal, so the triangle is right.
$a = 11$, $b = 60$, $c = 61$:
$121 + 3600 = 3721$ ✓ The left and right sides of this equation are equal, so the triangle is right.
$a = 26$, $b = 36$, $c = 45$:
$676 + 1296 = 2025$ ✗ The left and right sides of this equation are not equal, so the triangle is not right.
$a = 40$, $b = 75$, $c = 85$:
$1600 + 5625 = 7225$ ✓ The left and right sides of this equation are equal, so the triangle is right.
-
Identify the Pythagorean Triples.
HintsSometimes, the two sides of the simplified equation will not be equal. When that happens, the set is not a Pythagorean triple.
Be sure to carefully check that you have squared the terms correctly.
SolutionDamo wants to know if these sets of numbers are Pythagorean Triples. We can check this using the equation $a^2 + b^2 = c^2$, where $c$ is the largest number in the set. $a$ and $b$ are the other two numbers, and are interchangeable.
Looking at the first set, $5, 4$ and $6$, let's set:
$a = 5$
$b = 4$
$c = 6$ (because $6$ is the largest number)
We can substitute these values into the equation:
\begin{array}{rclcl} a^2 + b^2 & = & c^2 &|&\text{substituting} \\ 5^2 + 4^2 & = & 6^2 &|&\text{simplifying} \\ 25 + 16 & = & 36 &|&\text{simplifying} \\ 41 & = & 36 &|&\text{✗ the two sides of the equation are not equal} \\ \end{array}
Therefore this set of numbers does not satisfy the equation, and these numbers are not a Pythagorean Triple. So the statement in the question is false.
Similarly, for the second set, $12, 16$ and $20$:
$12^2 + 16^2 = 20^2$
$144 + 256 = 400$
Both sides of this equation are equal. Therefore the set is a Pythagorean Triple.
And for the third set, $15, 20$ and $25$:
$15^2 + 20^2 = 25^2$
$225 + 400 = 625$
Both sides of this equation are equal. Therefore the set is a Pythagorean Triple.