The Elimination Method

Basics on the topic The Elimination Method
Solving a System of Equation using the Elimination Method
In algebra, one common challenge is solving systems of linear equations - sets of equations with multiple variables. The elimination method is a powerful tool used to find these solutions, especially in real-world scenarios like budgeting or when working with coordinates.
The elimination method is an algebraic technique used to solve systems of linear equations. This method involves adding or subtracting equations to eliminate one of the variables, making solving the remaining variables easier.
The Elimination Method – Steps
The elimination method is particularly useful when equations in a system are not easily solvable using substitution. It involves aligning equations in such a way that adding or subtracting them results in one variable being eliminated, simplifying the system to one equation with one variable.
System of equations are sometimes referred to as simultaneous equations. This is because they represent a set of two or more equations that are solved together, sharing common variables, and solving them involves finding values for these variables that satisfy all equations in the system simultaneously.
| Step Number | Action | Example |
|---|---|---|
| 1 | Write down the system of equations. | $5x + y = 9$ $10x - 7y = -18$ |
| 2 | Manipulate one or both equations to align one variable. | Multiply the first equation by 7: $7(5x + y) = 7 \times 9$ $35x + 7y = 63$ |
| 3 | Rewrite the manipulated system. | $35x + 7y = 63$ $10x - 7y = -18$ |
| 4 | Add or subtract the equations to eliminate one variable. | Add the equations: $(35x + 7y) + (10x - 7y) = 63 - 18$ $45x = 45$ |
| 5 | Solve for the remaining variable. | $x = \frac{45}{45}$ $x = 1$ |
| 6 | Substitute the solved value into one of the original equations. | Substitute $x = 1$ into $5x + y = 9$: $5(1) + y = 9$ $y = 9 - 5$ |
| 7 | Solve for the second variable. | $y = 4$ |
| 8 | Write the final solution. | $x = 1$, $y = 4$ |
If you're interested in how graphing two equations can help find where they intersect to solve the system of equations, dive into the topic with the video Solving Systems of Equations by Graphing for a more detailed explanation.
The Elimination Method – Examples
Let's solve a system of equations using the steps for the elimination method:
Find the solution for $x$ and $y$.
$ \begin{array}{rcl} x + 2y & = & 6 \\ x - 2y & = & 2 \\ \end{array} $
Add the equations to eliminate $y$:
$(x + 2y) + (x - 2y) = 6 + 2$
$2x = 8$
Solve for $x$:
$x = \frac{8}{2}$
$x = 4$
Substitute $x = 4$ into the first equation to find $y$:
$4 + 2y = 6$
$2y = 2$
$y = \frac{2}{2}$
$y = 1$
The solution is:
$x = 4, y = 1$ and can be written as $(4, 1)$.
Let’s try another one!
Solve the system of equations.
$ \begin{array}{rcl} 7x + 2y &=& 24\\ 4x + y &=& 15\\ \end{array} $
Manipulate one equation to align one variable:
Multiply the second equation by -2: $-2(4x + y = 15)$
$-8x - 2y = -30$
Rewrite the manipulated system:
$7x + 2y = 24$
$-8x - 2y = -30$
Add the equations to eliminate $y$:
$(7x + 2y) + (-8x - 2y) = 24 - 30$
$-x = -6$
Solve for $x$:
$x = \frac{-6}{-1}$
$x = 6$
Substitute $x = 6$ into one of the original equations to find $y$:
Substitute into $4x + y = 15$:
$4(6) + y = 15$
$24 + y = 15$
$y = 15 - 24$
$y = -9$
The solution is:
$x = 6, y = -9$ and can be written as $(6, -9)$.
In addition to the Elimination Method, Using Substitution to Solve Systems of Linear Equations is another common algebraic method used!
The Elimination Method – Practice
The Elimination Method – Checking the Solutions
After solving a system of equations using the elimination method, it's important to verify that your solutions are correct. This involves substituting the solutions back into the original equations to ensure they satisfy both equations.
Suppose we solved a system and found that $x = 3$ and $y = 2$. The original equations were:
$\begin{array}{rcl} x+y&=&5\\ 2x-y&=&4\\ \end{array}$
Check:
- For Equation 1: Substitute $x = 3$ and $y = 2$ into $x + y = 5$.
$3 + 2 = 5$ which simplifies to $5 = 5$. This is true, so the solution satisfies the first equation.
- For Equation 2: Substitute $x = 3$ and $y = 2$ into $2x - y = 4$.
$2(3) - 2 = 4$ which simplifies to $6 - 2 = 4$ and further to $4 = 4$. This is also true, confirming the solution is correct for the second equation as well.
Try some checks on your own!
The Elimination Method – Summary
Key Learnings from this Text:
- The elimination method is used to solve systems of linear equations by eliminating one variable.
- It involves adding or subtracting equations to cancel out one of the variables.
- This method is especially useful when substitution is not straightforward.
- It's a practical skill in various real-world applications, like planning and geometry.
For a challenge, check out this video on Systems of Equations – Word Problems.
The Elimination Method – Frequently Asked Questions
Transcript The Elimination Method
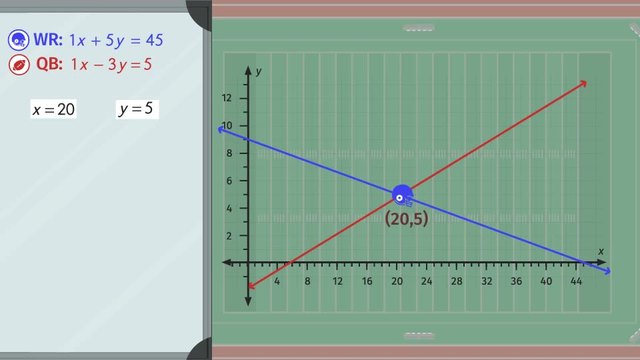
Last Friday, the 79ers football team lost really badly, so to avoid being embarrassed again, some of the players decide to stay after practice. The coach has given each of the players a linear equation to determine where they should be on the field. In order to be more successful in the next game and for the rest of the season, the players need to know how to solve linear systems of equations using the elimination method. The coach’s odd playbook calls for his wide receiver to run according to the linear equation ‘x’ plus 5y equals 45. Montana Jo, the star quarterback, needs to throw the ball with the linear equation 'x' minus 3y equals 5. But where will the ball and the receiver meet? Will they meet? Let’s help the receiver figure out where he’ll be able to catch the ball. To make things easier to see, let’s put a cartesian coordinate system over the football field. When using the elimination method on a system of linear equations, the goal is to ELIMINATE one of the variables, but there are some rules you’ll need to follow. If you notice, the coefficient for the variable ‘x’ in each linear equation is positive 1. However, the coefficients for the variable ‘y’ are 5 and negative 3, respectively. Here, we can use the elimination method for solving two linear equations. The goal is to manipulate, or change, an equation so that when we add the two equations together, we eliminate one of the variables. If we multiply the second equation by negative 1, we distribute to get negative ‘x’ plus 3y equals negative 5. "Now, if we add our two linear equations together, we’ll be able to eliminate the ‘x’s, giving us 0x plus 8y equals 40. Now that we’ve gotten rid of the variable ‘x’ in our equations, we can simply solve for ‘y’ using opposite operations."
Remember, always check your answers! You should end up with the same solution, regardless of which equation you use. Dividing both sides by 8 leaves us with ‘y’ equals 5. To find the value for ‘x’, we simply have to plug in 5 for ‘y’ in either equation. Let's use the first equation. So the solution to this system of linear equations is 'y' equals 5, and 'x' equals 20. Remember, always check your answers! Using the second equation and substituting our solutions for 'x' and 'y', we see that we're correct because 5 equals 5. Multiplying a linear equation by negative one is just one method of eliminating a variable. Let's take a look at the coach's second play to get a better idea. The wide receiver should run a '9 route', or the equation, ‘y’ equals 9, and the quarterback needs to throw the ball with the equation x minus 3y equals zero. Another way to eliminate a variable is to multiply one of the linear equations by a whole number constant. A whole number constant is just a number you multiply an equation by that allows you to add the two equations together. First, we have to find the lowest common multiple for the coefficient of either 'x' or 'y'. For this system of equations, we'll choose the variable 'y' because the first equation doesn't have an 'x'. For these equations, the lowest common multiple of ‘y’ and negative 3y is negative 3y. We could multiply the first equation by negative 3, but since we're looking for a number that will eliminate the negative 3y from the second equation, we can use the the additive inverse of -3, which is positive 3, to multiply the first equation by. Doing so gives us 3y equals 27. Just like the last time, we add the two linear equations together and we get ‘x’ equals 27. Aaaaand we already have our ‘y’!: 9! So our intersection point, and the solution to this system of linear equations, is (27, 9). Practice is going great so far, so the coach decides to give some of the other players a chance to prove themselves. The coach tells his backup quarterback, a young kid named Steve, to try out a play. The wide receiver is given the equation ‘x’ plus 2y equals 18, and the quarterback is given the route 2x plus 4y equals 8. We have to look for the lowest common multiple of 'x' or 'y'. If we choose 'x', what is the LCM of 1 and 2? If you said 2, you're exactly correct! Multiplying the first equation by 2 gives us 2x plus 4y equals 36. And since we need the additive inverse of 2x, we need to multiply the first equation by negative one, giving us negative 2x minus 4y equals negative 36. HUH?! BOTH of the variables have been eliminated! What do we do now? Let’s try to turn each of these equations into slope-intercept form to see what’s going on. The first equation in slope-intercept form is ‘y’ equals negative one-half ‘x’ plus 9, and the second is ‘y’ equals negative two over four ‘x’ plus two. If we simplify the slope in the second equation, we see that the two slopes are the same! We have parallel lines! And what do we know about parallel lines? That’s right. The lines will never, ever, ever meet. There is no solution to this system. Let's review our elimination method gameplan using our first example. The first thing we have to do is to decide which variable we want to eliminate. Next, we have to find the lowest common multiple of the coefficients of the variable we choose. Before adding the two equations make sure that we have the additive inverse of our chosen variable. Now that we've eliminated the variable 'x', we can solve for 'y'. Use the solution for 'y' to substitute and then solve for the variable 'x'. Remember, always check your answers! You should end up with the same solution, regardless of which equation you use. It’s gameday! But the star quarterback seems to be a little under the weather. The coach has no choice but to start his young, second quarterback, Steve. Steve has the play, but it’s the parallel play from practice! That play never works! He's gonna have to call an audible! And there he goes! I think the coach has found a new secret weapon!
The Elimination Method exercise
-
Determine which solution is true for a system of equations.
HintsYou can solve this system by using the elimination method.
In this method, you align two equations so that adding them together will eliminate one variable, making it possible to find the value of the other.
Notice that the equations have $y$ with an addition sign in one and a subtraction sign in the other. When you add the equations, these $y$ terms will cancel each other out, which means you can eliminate $y$ and solve for $x$ directly.
Substitution can be used to check if solutions are true. For example, if we had the equation $a+b=8$, and $a=3$ and $b=5$, we can substitute the values in for $a$ and $b$ so the equation is $3+5=8$. This is equal, so we know these values are true!
Solution$\begin{array}{rcl} x+y&=&10\\ x-y&=&4 \end{array}$
To find the solution, we can add these two equations directly to eliminate $y$ and solve for $x$, then substitute the value of $x$ into one of the equations to solve for $y$.
Let's solve this system:
Add the two equations:
$\begin{array}{rcl} x+y&=&10\\ +(x-y&=&4)\\ \hline 2x&=&14\\ x&=&7 \end{array}$
Now we substitute $x = 7$ into the first equation:
$\begin{array}{rcl} 7+y&=&10\\ y&=&3 \end{array}$
The solution to this system of equations is $x = 7$ and $y = 3$, or $(7,3)$.
-
Describe the elimination method for solving systems of linear equations.
HintsThe solution to a system of equations should be given as an ordered pair in $(x,y)$ format.
When multiplying an equation by a constant, all values on both sides of the equal sign must be multiplied by that value.
For example, if we wanted to change the $-x$ in this equation ($-x+3y=15$) to a positive $x$, the entire equation would be multiplied by $-1$ using the distributive property.
$(-1)(-x+3y=15)$
$x - 3y = -15$
When checking the solution to a system of equations, the ordered pair must make both equations true when substituted in for the values of $x$ and $y$.
SolutionWe are going to use the elimination method to solve a system of linear equations. In this method, we need to find a variable we can eliminate. We first want to create an additive inverse pair for one of our two variables.
Step 1: In this case, since the $x$ values have matching coefficients, we can work to eliminate them. To create an inverse pair of values, multiply the second equation by $\bf{-1}$ to get $x-9y=23$.
$~$
Step 2: Next, we will need to add the two equations together to eliminate a variable. The $x$ values will add to zero, so they cancel out, resulting in the equation $\bf{-16y=32}$.
$~$
Step 3: Now that we have an equation with a single variable, we can use inverse operations to isolate the variable. To isolate the $y$ variable, divide both sides by $\bf{-16}$ to get $y=-2$.
$~$
Step 4: Now that we know the value of $y$, we can solve for $x$. We can do this by substituting $\bf{-2}$ for $y$ in one of the original equations.
- Regardless of which of the original equations you choose, you will get the same result.
Step 5: Substituting $-2$ for $y$ in the first equation gives us $\bf{-x-7(-2)=9}$. Simplifying this equation results in $-x+14=9$. Solve this equation to get $x=5$.
- When solving the equation, you will need to make sure you end up with a positive x. One way to do this is to divide both sides of the equation by $-1$.
Step 6: The ball and the receiver will intersect at the point $(5,-2)$.
- Make sure to write the ordered pair as $(x,y)$ not $(y,x)$.
Step 7: To check this solution, substitute $5$ for $x$ and $-2$ for $y$ in both equations. Substituting into the first equation results in $\bf{-5-7(-2)=9}$. After simplifying we can see that the solution is correct for this equation since $9=9$. Substituting into the second equation results in $\bf{-5+9(-2)=-23}$. After simplifying we can see that the solution is correct for this equation since $-23=-23$.
-
Order the steps for solving a system of linear equations through elimination.
HintsThe first step requires one of the equations to be manipulated in order to cancel out one of the variables.
In this case, it is easier to eliminate the $x$ values.
Solve for $y$ prior to solving for $x$.
Solution- Multiply the first equation by $3$ to get a common multiple for the coefficients of $x$.
$-3x+21y=6$
- Add the equations:
- Solve for $y$:
- Substitute $2$ in for $y$ in the first equation:
- Solve for $x$:
- The receiver and the ball will intersect at the point $(12,2)$.
-
Apply the steps to solve a systems of equations with elimination method.
HintsOne solution: This type of system has lines that intersect at one point, and using elimination will give you a single pair of $x$ and $y$ values that solve both equations.
No solution: The lines are parallel and never meet; elimination will lead to a false statement, like $0 = 5$, indicating that there is no common solution.
Infinite solutions: The lines overlap exactly, and elimination will result in a true statement regardless of $x$ and $y$, like $0 = 0$, showing that any point on the line solves the system.
When multiplying an equation by a constant, make sure to multiply everything on both sides of the equation to get an equivalent equation.
This is known as the Distributive Property.
When adding an expression with opposite coefficients such as $-4x$ and $4x$, the $x$ values are eliminated, so $-4x+4x=0$.
SolutionThis system of equations has no solution.
$\begin{array}{lcr} x+2y&=&4\\ 3x+6y&=&18 \end{array}$
- Multiply the first equation by $-3$:
$~$
$\begin{array}{lcr} -3x-6y&=&-12\\ 3x+6y&=&18 \end{array}$
- Add the equations together to notice that the $-3x$ and $3x$, as well as the $-6y$ and $6y$ will cancel each other out, resulting in $0$ on that side of the equal sign.
- Because $0$ is not equal to $6$, there is no solution.
-
Review evaluating expressions and finding the least common multiple of two numbers.
HintsThe least common multiple of two numbers is the smallest number that they both divide evenly into. For example, the least common multiple of $6$ and $8$ is $24$. To get this answer, start by listing some of the multiples of each number.
$\bf{6}$: $6, 12, 18, 24, 30$
$\bf{8}$: $8, 16, 24$
As soon as you find a common multiple, you can stop making your list since we are looking for the least common multiple.
Use the distributive property to simplify expressions in the form $a(b+c)$. For example, if you have the expression $3(x+4)$, multiply each value inside the parentheses by $3$. This results in $3(x)+3(4)$. This expression simplifies to $3x+12$.
In order to evaluate an expression, substitute (replace) the given value of the variable into the expression and simplify. For example, to evaluate the expression $x+5$ given that $x=2$, replace the $x$ with $2$ to get $2$$+5 = 7$.
Solution- The least common multiple of $3$ and $7$ is $21$ since $3(7)=21$ and $7(3)=21$
- Evaluating the expression $-3x+4$ for $x=-8$: Substitute $x$ for $-8$ in the expression: $-3(-8)+4 = 24+4 = 28$
- The least common multiple of $3$ and $6$ is $6$ since $3(2)=6$ and $6(1)=6$
- Evaluating the expression $-4x+5$ for $x=\left( \frac{1}{2} \right)$: $-4\left( \frac{1}{2} \right)+5=-2+5=3$
-
Solve the real-word problems using systems of linear equations.
HintsPay careful attention to keywords such as
- combined total: adding
- twice: multiplied by $2$
- more than: adding
When you are solving using the elimination method, it is helpful to have the variables line up, like this:
$\begin{array}{rcl} x+3y&=&18\\ -x-4y&=&-25 \end{array}$
To find the perimeter of a rectangle, add all the sides together. Since there are two pair of equal sides on a rectangle, you will need to add twice the length and twice the width, so formula looks like this:
$P = 2L+2W$
SolutionLast season, two running backs on the college football team rushed for a combined total of $1,050$ yards. Jamal rushed $2$ times as many yards as Titon. How many yards were rushed by each player?
Let $J =$ the number of yards rushed by Jamal
Let $T =$ the number of yards rushed by Titon
The first equation is:
$J+T=1,050$
Since Jamal rushed $2$ times as many yards as Titon, the second equation is:
$J=2T$
First, we need the two equations to be in the same format, so subtract $2T$ from both sides of the equation to get:
$J-2T=0$
In order to eliminate the $J's$, multiply the second equation by $-1$:
$-1(J-2T=0)$
$-J +2T=0$
Add the equations together and solve!
$3T=1,050$
$T=350$
Substituting $T=350$ into the first equation $J+T=1,050$, and solve for $J$:
$J=700$
Jamal rushed $700$ yards and Titon rushed $350$ yards.
$~$
On Monday, Samuel bought $10$ bottles of coconut water and $5$ mangos for his club meeting for $\$16.50$. It turns out that the mangos were more popular than the coconut water. On Tuesday he bought $5$ bottles of coconut water and $10$ mangos for a total of $\$14.25$. How much was each bottle of coconut water?
Let $C=$the price of the coconut water
Let $M=$the price of the mangos
To get the cost, we need to multiply the number of each item by the price of each item:
Monday: $10C+5M=16.50$
Tuesday: $5C+10M=14.25$
In order to get the $C's$ to cancel, multiply the second equation by $-2$:
$-2(5C+10M=14.25)$
$-10C-20M=-28.50$
Add the equations together and solve for $M$:
$-15M=-12.00$
$M=0.8$
Substituting $M=0.8$ into the original equation for Tuesday and solve for $C$:
$5C+10(0.8)=14.25$
$C=1.25$
Each bottle of coconut water cost $\$1.25$.
$~$
The perimeter of a rectangular garden is $62$ feet. The length is $1$ foot more than twice the width. Find the dimensions of the garden.
We know that the formula for the perimeter of a rectangle is $P=2L+2W$. We also know that $P=62$, so we can substitute 62 for $P$ in the formula:
$62=2L+2W$
Since we have two variables in our equation, we will need another equation relating length ($L$) and width ($W$) to solve this problem.
We are given that The length is $1$ foot more than twice the width so our second equation is:
$L=1+2W$
To use the elimination method, we need the two equations to be in the same format. We can subtract $2W$ from both sides on the second equation and flip the first equation to get:
$L-2W=1$
$2L+2W=62$
Add the equations together and solve for the missing variable.
$3L=63$
$L=21$
Using the second equation $L=1+2W$, substitute $21$ for $L$ to solve for $W$:
$21=1+2W$
$W=10$
The length of the rectangle is $21$ feet and the width of the rectangle is $10$ feet.
















Please Please Pleeeeeease keep doing this. i am absouloutely loling about you guys recreating the old 49ers roster you avoided copyright with: Montana Joe (Joe Montana and a young kid named steve (Steve Young)