Solving Rational Equations
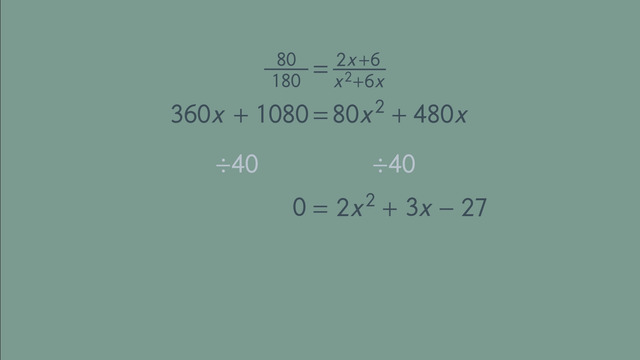

Basics on the topic Solving Rational Equations
A rational equation is an equation in which one or more terms is a rational expression – a fraction in which the numerator and/or the denominator are polynomials. When solving a rational equation, a method known as cross multiplication is used to eliminate the denominators on both sides of the equation. For instance, using cross multiplication, we can rewrite the equation (3/x) = (6/x+4) as 3(x+4) = 6x, and then solve for x. Learn more about how to solve rational equations by helping Grandpa Lindbergh and his tour group survive on a deserted island. Common Core Reference: CCSS.MATH.CONTENT.HSA.REI.A.2
Transcript Solving Rational Equations
On a tour of the Caribbean, Grandpa Lindbergh had to make an emergency landing, leaving his tour group on a deserted island. Being a resourceful group, they know they need a few things to survive the first night: shelter, a fire and food plus the knowledge of Solving rational equations to distribute the work efficiently. Luckily, they crashed in the morning, so they have a little while to work. However, time’s-a-tickin’ and they’re not sure if they’ll be able to finish all the tasks before sundown. Mike volunteers to find food on the island, General Good collects leaves for the roof, leaving Jasmine and Grandpa to collect wood for the fire.
Setting up a rational equation
After a while, Jasmine comes back with 10 pieces of wood, Grandpa returns 10 minutes later with 15 pieces, but they’re not quite sure how long they were off collecting wood. We call the time it took for Jasmine to collect 10 pieces of wood 'x'. Since Grandpa Lindbergh came back 10 minutes later than Jasmine, we can say that Grandpa took 'x' + 10 minutes to gather 15 pieces of wood. Since they collected wood at the same rate, they can set up a rational equation to help them determine the time it took them to complete the task.
Solving a rational equation
To solve this problem, we can use a method called cross-multiplication. We simply have to multiply the numerators on one side of the equal sign by the denominators on the other side of the equal sign. Like this.Then we use PEMDAS and opposite operations to isolate the variable and solve. Distribute the 10 giving us 10x + 100, substract 10x from both sides of the equation and finally divide both sides by 5 to give us our answer.
So, Jasmin collected 10 pieces of wood in 20 minutes which averages out to one piece every two minutes. Grandpa Lindbergh collected wood at the same rate. He gathered 15 pieces in 30 minutes which is also one piece every two minutes To make sure they have enough for the night, Jasmine goes off to collect more wood.
Setting up the rational equation
In the meantime, General Good comes back from gathering leaves, which Grandpa and General Good weave together for a roof so the group has some shelter to protect them from the elements. In order to finish the shelter before sundown, Grandpa and General Good need to weave together 80 leaves in 3 hours, which is the same as180 min.
Solving the rational expression
Although they can weave leaves at the same unknown rate of 1 over 'x', Grandpa needs a bit of a breather after every leaf, changing his rate to 1 over x plus 6. How long do they have to weave each leaf? To solve this rational equation, we have to find a common denominator first because we have to sum the numbers on the right side of the equation. To find the common denominator, we multiply the numerator and denominator of the first fraction by the denomiator of the second fraction, (x+6), and vice versa. Next, we have to use the Distributive Property, giving us 'x' plus 6 divided by the quantitiy x squared plus 6x plus 'x' divded by quantity x squared plus 6x. Now that we have common denominators, we can simply add the numerators. From here, we can cross-multiply, as we did in the previous example. Just use the Distributive Property again. All terms are divisible by 40, so we divide both sides by 40.
Next, we bring the equation into standard form and simplify by combining like terms. For our last step, we can factor the equation, leaving us with (2x+9) times (x-3). To solve for 'x', we use the Zero Product Property and set both factors equal to zero. Finally, we can solve for 'x' using opposite operations. Negative time?!? Remember, when solving word problems with rational expressions, you not only have to plug your answers to check your work but you also have to think about the solution and whether or not it makes sense.
So, General Good has to weave at least 1 leaf every 3 minutes, whereas Grandpa Lindbergh has to weave 1 leaf every 9 minutes in order to finish the roof on time. Together, they can weave 4 leaves every 9 minutes. Everyone’s glad that they were all able to finish the tasks before sundown, but they’re famished!
By the way - Where’s Mike? More importantly, where’s the food? Wait, where did Mike get fast food? Maybe they should have looked around the island a bit before trying to play survivor.
Solving Rational Equations exercise
-
Describe how to solve the rational equation.
HintsHere you see an example of the distributive property.
To solve equations use opposite operations:
- The opposite operation of addition is subtraction and vice versa.
- The opposite operation of multiplication is division and vice versa.
Check your solution by putting it into the starting equation.
SolutionThe rate is the number of wood pieces divided by the needed time. Let $x$ be the time it takes Jasmine to collect $10$ pieces of wood.
Thus we get the rate
$\frac{10~\text{wood pieces}}{x~\text{minutes}}$
for Jasmine and, with the same measures,
$\frac{15}{x+10}$
for Grandpa Lindbergh. Because the rates agree we get the following rational equation:
$\frac{10}{x}=\frac{15}{x+10}$.
First, we cross multiply to get
$15x=10(x+10)$.
Using the distributive property gives us $15x=10x+100$. From now on we use opposite operations to isolate $x$:
$\begin{array}{rcl} 15x & = & ~10x+100\\ \color{#669900}{-10x} & &\color{#669900}{-10x}\\ 5x & = & ~100\\ \color{#669900}{\div5} & & \color{#669900}{\div5}\\ x & = & ~20 \end{array}$
Lastly, let's check the solution $\frac{10}{20}=\frac12=\frac{15}{20+10}$ $~~~~~$✓
Thus we can conclude that Jasmine takes $20$ minutes to collect $10$ pieces of wood, while Grandpa Lindbergh takes $30$ minutes to collect $15$ pieces of wood.
-
Calculate how much time it takes General Good and Grandpa Lindbergh to weave $1$ leave.
HintsYou can only add or subtract fractions with the same denominator.
Use FOIL multiplication to check that the quadratic term equals $(2x+9)(x-3)$.
Put the solutions in the starting equation to check them. They must satisfy this equation.
SolutionFirst, let's have a look at the rate for all leaves: together Grandpa and General Good need to weave together $80$ leaves in $3$ hours, it's $180$ minutes. This gives us the rate $\frac{80}{180}$.
The rate for General Good is, $\frac1x$, and for Grandpa, $\frac1{x+6}$. Together means „$+$“. So we get $\frac1x+\frac1{x+6}$.
Now we can state the equation
$\frac{80}{180}=\frac{1}{x}+\frac{1}{x+6}$.
To use cross multiplying, we first have to sum both fractions on the right side of the equations. For this we need the common denominator, it's $(x)(x+6)$. Now we enlarge the left fraction by $x+6$ and the right one by $x$:
$\frac{80}{180}=\frac{1(x+6)}{x(x+6)}+\frac{1(x)}{(x+6)(x)}$.
With the distributive property we get
$\frac{80}{180}=\frac{x+6}{x^2+6x}+\frac{x}{x^2+6x}$.
We add fractions with the same denominator by just adding the numerators. Further on we can combine like terms:
$\frac{80}{180}=\frac{x+6+x}{x^2+6x}=\frac{2x+6}{x^2+6x}$.
Now we're able to cross multiply:
$180(2x+6)=80(x^2+6x)$.
Once again with the distributive property we can multiply out
$360x+1080=80x^2+480x$.
Dividing by $40$ this is equivalent to
$9x+27=2x^2+12x$.
Using opposite operations and combining like terms lead to a quadratic equation
$\begin{array}{rclll} 9x+27 & = & ~2x^2+12x\\ \color{#669900}{-9x} & &\color{#669900}{-9x}\\ 27 & = & ~2x^2+12x-9x&|&\text{combining like terms}\\ 27 & = & ~2x^2-3x\\ \color{#669900}{-27} & & \color{#669900}{-27}\\ 0 & = & ~2x^2-3x-27 \end{array}$
We can factorize this equation as follows $(2x+9)(x-3)=0$.
Any product is zero if one of the factors is zero. So we have to solve the following equations
$\begin{array}{rclll} 2x +9& = & ~0\\ \color{#669900}{-9} & &\color{#669900}{-9}\\ 2x & = & ~-9\\ \color{#669900}{\div 2} & & \color{#669900}{\div 2}\\ x & = & ~-\frac92 \end{array}$
and
$\begin{array}{rclll} x-3 & = & ~0\\ \color{#669900}{+3} & &\color{#669900}{+3}\\ x & = & ~3 \end{array}$
You can check your solution, but before you do so, have a look to see if the solutions are meaningful. $x$ represents a time. So $-\frac92$ isn't a meaningful solution at all. The only meaningful solution is $x=3$.
-
Determine the rate of gathering berries.
HintsLet $x$ be the time Lisa needs to gather $120$ berries. Then the rate is given by $\frac{120}x$.
Determine the rate for Tim similarly.
Keep in mind that the rates must agree.
Check your solution: the rate for Lisa as well as for Tim must be the same with this solution.
SolutionHere we take $x$ for the time Lisa needs to gather $120$ berries. The rate is the number of berries divided by the needed time:
$\frac{120}{x}$.
Similarly we establish the rate for Tim. Tim takes $15$ minutes more than Lisa, or $x+15$. During this time he gathers $210$ berries in total. So we get the rate
$\frac{210}{x+15}$.
The fact that the rates agree leads to the equation
$\frac{120}{x}=\frac{210}{x+15}$.
To get the rate, we have to solve this equation:
- Cross multiply to $210x=120(x+15)$.
- Use the distributive property to get $210x=120x+1800$.
- Solve the equation using opposite operations:
So the rate is $\frac{120}{20}=6$ berries per minute.
We can check the solution as well: $\frac{210}{20+15}=\frac{210}{35}=6$ $~~~~~$✓
-
Calculate how much time Jason and Naya can spend to tie $1$ bouquet.
HintsThe rate is given by the relation between the number of bouquets and time in minutes.
So the $2$ hours left for $20$ bouquets is given by the rate: $\frac{20}{120}=\frac16$.
The equation you have to solve is given by $\frac16=\frac1x+\frac1{x+5}$.
Enlarge the left fraction by $x+5$ and the right one by $x$.
You get two solutions but only one is meaningful. This is the maximum time for Naya. Just add $5$ minutes to get the maximum time for Jason.
SolutionFirst we establish the equation to solve:
- The number of bouquets tied in $2$ hours gives us the rate $\frac{20}{120}=\frac16$.
- The rate of Naya is given by $\frac1x$.
- The one of Jason is given by $\frac1{x+5}$, because Jason takes $5$ minutes more than Naya.
- The total rate is $\frac1x+\frac1{x+5}$.
$\frac16=\frac{1}{x}+\frac{1}{x+5}$.
Next we enlarge the left fraction on the right side by $x+5$ and the right one by $x$ to get the common denominator $(x)(x+5)=x^2+5x$:
$\frac16=\frac{1(x+5)}{x^2+5x}+\frac{1(x)}{x^2+5x}=\frac{2x+5}{x^2+5x}$.
Now we use cross multiplication:
$6(2x+5)=x^2+5x$,
which is, using the distributive property, equivalent to
$12x+30=x^2+5x$.
Using opposite operations and combining like terms leads to a quadratic equation
$\begin{array}{rclll} 12x+30 & = & ~x^2+5x\\ \color{#669900}{-12x} & &\color{#669900}{-12x}\\ 30 & = & ~x^2+5x-12x&|&\text{combining like terms}\\ 30 & = & ~x^2-7x\\ \color{#669900}{-30} & & \color{#669900}{-30}\\ 0 & = & ~x^2-7x-30 \end{array}$
We can factor this equation as $(x+3)(x-10)=0$.
Any product is zero if one of the factors is zero. So we have to solve the following equations:
$\begin{array}{rclll} x +3& = & ~0\\ \color{#669900}{-3} & &\color{#669900}{-3}\\ x & = & ~-3 \end{array}$
and
$\begin{array}{rclll} x-10 & = & ~0\\ \color{#669900}{+10} & &\color{#669900}{+10}\\ x & = & ~10 \end{array}$
$x=-3$ isn't a meaningful solution because $x$ represents a time. So the only solution is $x=10$.
Thus we can conclude that Naya has at most $10$ minutes and Jason $10+5=15$ minutes to make one bouquet.
-
Set up the rational equation.
HintsThe rate is the number of wood pieces divided by the needed time.
Let $x$ be the time Jasmine needs to collect $10$ pieces of wood. So Grandpa Lindbergh needs $10$ minutes more, or $x+10$.
The rate for Jasmine is $\frac{10}x$.
Both rates must agree.
SolutionTo establish en equation corresponding to a word problem, we first assign variable(s) to the desired quantity.
So, we assign $x$ to the time Jasmine needs to collect $10$ pieces of wood. The corresponding rate is then $\frac{10}x$.
Grandpa Lindbergh takes $10$ minutes more than Jasmine, ior $x+10$, for $15$ pieces of wood. This gives us the rate
$\frac{15}{x+10}$.
Those rates have to agree, giving us the equation
$\frac{10}x=\frac{15}{x+10}$.
-
Solve the rational equations.
HintsRemember how to find a solution to a rational equation:
- First, add or subtract fractions on one or both sides of the equation if it's necessary.
- Cross multiply to get a non rational equation.
- Solve the resulting equation using opposite operations.
- If you get a quadratic equation you have to factor it.
You can also use the formula to solve quadratic equations:
$ax^2+bx+c=0$
$x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}$.
Use the following factorizations:
- $3x^2-6x-24=(3x-12)(x+2)$
- $x^2-2x-24=(x+4)(x-6)$
Three equations have two solutions and only one has one solution.
SolutionHere is a general procedure for solving rational equations:
- First, add or subtract fractions on one or both sides of the equation if it's necessary.
- Cross multiply to get a non-rational equation.
- Solve the resulting equation using opposite operations.
- If you get a quadratic equation you have to factor it.
Let's start with $\frac x{x-2}=\frac1{x+2}$:
- Cross multiplying gives us $x-2=x(x+2)=x^2+2x$.
- Next, we transform this equation, adding $2$ and subtracting $x$ to $x^2+x-2=0$.
- Use the formula to solve quadratic equations: $x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}$, with $a=1$, $b=1$ and $c=-2$.
So we get two solutions: $x=\frac{-1+3}2=\frac22=1$ and $x=x=\frac{-1-3}2=\frac{-4}2=-2$.
The next example is given by $\frac6{x}=\frac{3x}{x+4}$.
- Cross multiplying gives us $6(x+4)=6x+24=3x^2$.
- Next, we transform this equation; subtracting $6x$ as well as $24$ gives us $3x^2-6x-24=0$.
- You can factorize the quadratic term as follows: $(3x-12)(x+2)$.
- Lastly, we have to solve two equations:
and
$\begin{array}{rclll} x+2 & = & ~0\\ \color{#669900}{-2} & &\color{#669900}{-2}\\ x & = & ~-2 \end{array}$
$~$
Next, we have another equation with the variable in the numerator and the denominator on both sides: $\frac{x}{x+4}=\frac{x-4}{x+2}$
- Cross multiplying gives us $x(x+2)=(x+4)(x-4)$.
- Using the distributive property and FOIL multiplication gives us $x^2+2x=x^2-16$.
- Subtracting $x^2$ on both sides leads to $2x=-16$.
- Lastly, we divide by $2$ to get $x=-8$.
Let's now look at $\frac14=\frac1x+\frac1{x+6}$
- Add the fractions on the right side. For this enlarge the left one by $x+6$ and the right one by $x$ to get $\frac{1(x+6)}{x(x+6)}+\frac{1(x)}{(x+6)(x)}=\frac{2x+6}{x^2+6x}$.
- Cross multiplying leads to $x^2+6x=4(2x+6)=8x+24$.
- Next, we transform this equation: first subtract $8x$, combine the like terms, and after subtract $24$ to get $x^2-2x-24=0$.
- Factor this equation to $(x+4)(x-6)=0$.
- Lastly, we have to solve two equations:
and
$\begin{array}{rclll} x-6 & = & ~0\\ \color{#669900}{+6} & &\color{#669900}{+6}\\ x & = & ~6 \end{array}$