Solving Proportions
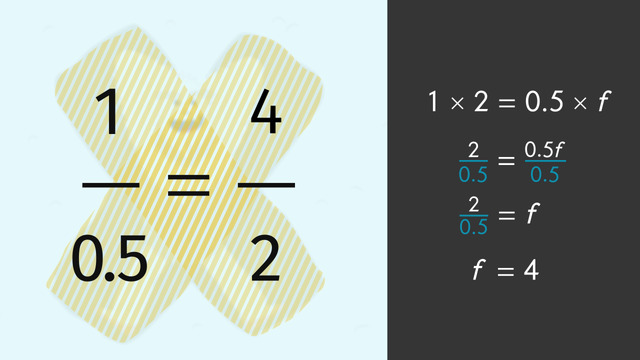

Basics on the topic Solving Proportions
To understand proportions, you must understand ratios. Ratios are used to compare quantities. You can write a ratio to look like a fraction. For example the ratio one to two can be written as ½.
How do ratios differ from fractions? Fractions are used to compare a part of something to the whole of that same something. Ratios compare quantities, like 3 apples for every 4 oranges. Are you wondering how all of this is connected to proportions? Two equal ratios make a proportion. Proportions are very useful to solve for unknown amounts because you can use cross product, which is also known as cross multiplication.
To use cross product, multiply the numbers that are diagonally across the equal sign. For all proportions, their cross products are always equal. Let’s consider an example. If there are 3 apples for every 4 oranges, and there are 96 oranges, how many apples are there? You can set this up as a proportion. Make sure the numbers for apples are in the same position in the fraction, as well as the numbers for the oranges. This means, be consistent with the quantities you write in the numerator and denominator. If you put apples in the numerators of one ration do so with the other. After you set up the proportion and calculate the equal cross products, use algebra to solve for the unknown quantity. FYI – there are 72 apples.
You may be surprised how useful setting up proportions and using cross product to solve for unknown amounts can be. You can use this strategy to solve all kind of problems as you progress with your studies of algebra and geometry. To learn more about proportions, watch this video.
Solve unknown quantities using proportions CCSS.MATH.CONTENT.HSA.CED.A.1
Transcript Solving Proportions
Andretti the Yeti is worried. Why's he worried? Well, in two hours, he has a date with Nettie the Bodacious Yeti and it's just started to snow.
Snow? What's a little snow when you have a date with the love of your life? Well, Rule #5 of the Yeti Handbook states, if the snow is four feet deep, you can't be outside. Andretti doesn’t know if he'll be able to make it to her place.
The Yeti Weatherman reports the snow will fall at a constant rate of one foot of snow per half hour for the next several hours. Nettie is expecting him in 2 hours. In two hours, will the height of the snow be less than four feet?
Setting up a Proportion or two equal Ratios
Let’s help him figure this out! We can set up a proportion, also known as two equal ratios. Ratios compare quantities. When you set up a proportion, the numerators and denominators of each ratio must contain the same variable.
Our proportion will contain ratios comparing the amount of snow in feet per hour. Let's look at the given information. We know it's snowing one foot per half hour. How deep will the snow be in two hours?
Solving Example Proportion
Andretti the Yeti has an idea of how to solve this problem. He left us a hint in the snow. To solve for the unknown quantity of snow, we'll use cross multiplication, also known as cross product.
Don't confuse cross multiplication with cross cancellation. You use cross cancellation to make multiplying fractions easier.
Set the two cross products equal to each other. 1 · 2 = 2 and 0.5 · f = 0.5f. We are left with 2 = 0.5f.
To solve, divide both sides by 0.5. f = 4. At this rate, in two hours the snow will be four feet deep. Oh no! That won't work. What should Andretti do?
Example Proportion 2
He should then plan to arrive earlier for his date! He doesn't want to break the Yeti rule, so he needs to get there before the snow is 4 feet deep. In how many hours will the snow be only three and one-half feet deep?
Using the same ratio, let’s set up another proportion, this time to solve for the unknown quantity of hours. We will solve this proportion just like we did before, using cross multiplication.
h = 0.5 · 3.5. To get to Nettie’s place before the snow is too deep, Andretti should plan to meet with her in 1.75 hours, or an hour and three-quarters. He needs to leave fifteen minutes earlier than originally planned.
Nettie is finally ready for their date. Poor Andretti, he followed Yeti Rule number 7 and waited outside of her house since he was too early.
Solving Proportions exercise
-
Manipulate the formula to get the value for $f$.
HintsHere you can see an example of cross-multiplication:
$\frac42=\frac a3~\leftrightarrow~4\times 3=2\times a$
You can solve an equation by using opposite operations:
- the opposite operation of addition is subtraction and vice versa
- the opposite operation of multiplication is division and vice versa
SolutionAn equation representing a proportion has the form: $\frac ab=\frac cd$.
You have to know three values to get the solution for the unknown value. First of all, you cross-multiply the terms: $a\times d=c\times b$.
Afterwards you can solve this equation by dividing.
Now, let's have a look at the equation:
$\frac1{0.5}=\frac f2$
- first cross-multiply to $1\times 2=0.5\times f$
- divide by $0.5$ to get the solution, $f=4$
-
Determine the depth of the snow after two hours.
HintsIn order to solve equations you need to use opposite operations.
The equation $2x=6$ can be solved by dividing by $2$.
A ratio like four cookies for two yetis can be written as $\frac42$.
SolutionLet's have a look at the given information:
The snow gets one foot deeper every half an hour.
This can be written as $\frac1{0.5}$. The snow gets $f$ feet deeper in two hours, which results in $\frac f2$.
We can write the proportion:
$\frac1{0.5}=\frac f2$
Now we can cross multiply:
$1\times 2=0.5\times f$
In a last step, we can divide by $0.5$ to get the solution:
$f=\frac2{0.5}=4$
-
Solve the following proportions.
HintsCross-multiplication:
$\frac ab=\frac cd \Leftrightarrow a\times d=c\times b$
Depending on the value you want to determine, you will have to use the opposite operation.
To solve the equation $2\times x=8$, you will have to divide by $2$ to get the solution $x=4$.
You can check your result by plugging it into the given proportion.
SolutionYou can use cross-multiplication to solve for unknown values in a proportion: $\frac ab=\frac cd$.
Follow the steps:
- cross-multiply: $a\times d=c\times b$
- solve the equation by using opposite operations
- cross-multiply: $1\times a=4\times 2$
- result is $a=8$
- check: $\frac12=\frac48=\frac{4\div4}{8\div4}=\frac12$ $\surd$
- cross-multiply $1\times 4=b\times 2$
- divide by $2$ to get the solution $b=4\div 2=2$
- check: $\frac12=\frac24=\frac{2\div2}{4\div2}=\frac12$ $\surd$
- cross-multiply $c\times 4=9\times 2$
- divide by $4$ and get $c=18\div 4=4.5$
- check: $\frac{4.5}2=\frac{4.5\times 2}{2\times 2}=\frac94$ $\surd$
-
Determine the number of days Freddy the yeti has to save his pocket money.
HintsTo figure this out, you can set up a proportion.
You already know the proportion $\frac{3.5}7$
- $3.5$ is his allowance for each week
- $7$ is the number of days per week
The number of days are he needs to save money are unknown.
Represent the unknown number of days with a variable, and write it in the denominator.
Cross-multiply to solve for the unknown value.
$\frac ab=\frac cd \Leftrightarrow a\times d=c\times b$
You can check the solution by plugging it into the proportion:
$\frac {3.5}7=\frac ab$
- $a$ is the amount of money needed to fulfill a wish
- $b$ is the unknown number of days
SolutionEach proportion is written in this form:
$\frac ab=\frac cd$
You can check each solution by plugging it into the proportion:
$\frac {3.5}7=\frac ab$
- $a$ is the amount of money needed to fulfill a wish
- $b$ is the unknown number of days
- $\frac {3.5}7=\frac {14}b$
- cross-multiplication results in $3.5 \times b=14\times 7$
- dividing by $3.5$ gives us $b=28$
- Freddy has to save his pocket money for $28$ days.
- $\frac {3.5}7=\frac {5}b$
- cross-multiplying results in $3.5 \times b=5\times 7$
- dividing by $3.5$ gives us $b=10$
- Freddy has to save his pocket money for $10$ days.
- $\frac {3.5}7=\frac {40}b$
- cross-multiplying results in $3.5 \times b=40\times 7$
- dividing by $3.5$ gives us $b=80$
- Freddy has to save his pocket money for $80$ days.
- $\frac {3.5}7=\frac {3}b$
- Cross-multiplication results in $3.5 \times b=3\times 7$
- dividing by $3.5$ gives us $b=6$
- Freddy has to save his pocket money for $6$ days.
-
Find the correct proportion.
HintsA proportion can be written as a fraction.
For example, six scoops of ice-cream for three yetis can be written as $\frac63$.
Keep in mind that for this ratio the amount of time is listed in the denominator.
SolutionWhat do we know?
- The snow gets one foot deeper every half an hour. We can write this as a ratio: $\frac1{0.5}$.
- In order to calculate the number of hours $h$ for the given depth of 3.5 feet we can write the ratio: $\frac {3.5}h$.
$\frac1{0.5}=\frac {3.5}h$
By cross-multiplying we can solve for the unknown value:
$1\times h=0.5\times 3.5$
The result is $h=1.75$. Andretti has to start in $1.75$ hours.
-
Determine the number of hours till the snow is four feet deep.
HintsKeep in mind that we have to solve two proportions.
In the first proportion, the depth is unknown.
In the second proportion, the number of hours is unknown.
You have to subtract the depth of snow after two hours from four. This is the depth you have to use for the second equation.
Keep in mind that you have to add two hours to the solution of the second equation.
SolutionTo solve this problem, we will have to follow two steps:
- First of all we will have to determine the depth of the snow after two hours.
- If the snow isn't four feet deep yet, we will have to use a second proportion.
If the snow gets $0.25$ feet deeper every half an hour, how deep will the snow be after two hours?
- first proportion: $\frac{0.25}{0.5}=\frac f2$
- cross-multiplying results in $0.25\times 2=f\times 0.5$
- divide by $0.5$ to get $f=1$
The snow isn't deep enough, so we'll have to determine how long it will take for three more feet of snow to fall ($4-1$).
- second proportion: $\frac{0.75}{0.5}=\frac 3h$
- cross-multiplication: $0.75\times h=3\times 0.5=1.5$
- divide by $0.75$ to get $h=1.5\div 0.75=2$
Therefore we know that after four hours ($2+2$) the snow is four feet deep.
















One of my favorite videos!