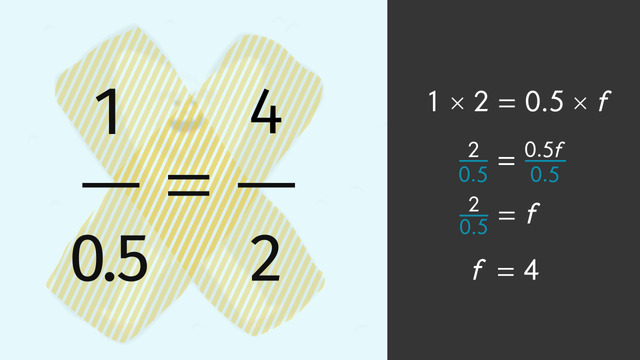Solving Percent Equations
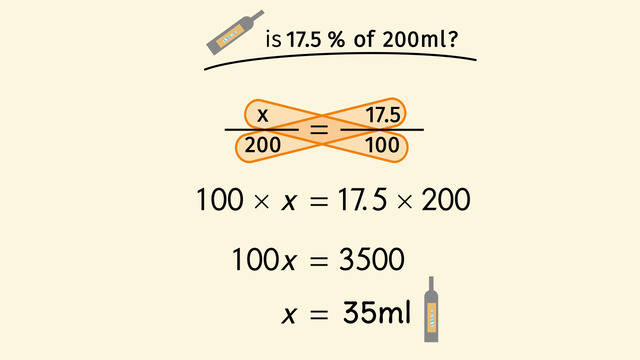

Basics on the topic Solving Percent Equations
Summary of Solving Percent Equations
To calculate percent equations, it’s helpful to use what you know of ratios and proportions. To solve for unknown values when calculating percent of a number equations, use the proportion:
Part/whole = percent/100.
Notice the second ratio is the fraction that represents a percent.
What is the part and whole? For example, if you eat 3 slices of pizza, the part you eat is equal to 3 slices and the whole pie is equal to 4 slices. To solve for any unknown value in the proportion, you can use cross product.
To use cross product, also known as cross multiplication, imagine a cross written across the proportion a/b = c/d, when there are two equal ratios making a proportion, the products of the cross values are equal, so for this example, ad = bc.
Using cross product to set up an equation then use opposite operations to isolate the variable.
For some equations, not all the information will be provided in percent form, so before you can set up an equation using cross product, you may have to convert fractions and decimals to percent.
Just to refresh your memory:
- To convert a decimal to a percent, multiply by 100 then add the percent sign.
- To convert a fraction to a percent, create an equivalent fraction with 100 in the denominator.
To learn more about percent equations, take a look at what Richard the Mange is making in his lab. Convert between formats to solve percent equations.
Common Core
CCSS.MATH.CONTENT.HSA.SSE.B.3
Let's practice: Percent Equation Exercises
With the following exercises on the topic of percent equation, you can test whether you have understood everything. Test your knowledge now!
Note: The conversions from milliliters to fluid ounces are approximate, as 1 milliliter is approximately equal to 0.0338 fluid ounces.
Transcript Solving Percent Equations
Richard the mage has fallen head over heals for the beautiful princess, Ms. Morgaine. He's madly in love, but she doesn't like him one bit. He wants to make his great-grandmother's love potion number 9 to make the princess fall in love with him forever.
To brew potion number 9, he needs to calculate a few percent equations, as percents are part of the recipe. To make 200 ml of the potion, which is one full dose, he'll need to mix these ingredients:
- 20% honey
- ½ of a bat wing
- 50 teardrops of love
- 17.5% unicorn horn extract
Percent Equation Example 1
Some of these are listed as percentages of the full 200 ml potion. In particular, the honey and unicorn horn extract. How can he figure out how much of each ingredient he must use?
So if honey makes up 20% of the whole potion, we must find 20% of 200ml. We can use the formula, part over whole equals percent over 100, to start answering this question.
For the amount of honey, which is unknown, we use x. Now let's substitute: 20 percent of the love potion is honey, so we'll substitute percent with 20. And since 200ml is the full amount of the potion, we substitute 200 for the whole. To find the part, which is our unknown, we can call it x.
We can use cross multiplication to get rid of the denominators. That gives us the equation 100 · x = 20 · 200. We can simplify this to 100x = 4000.
Finally, we can solve for x by dividing both sides by 100. We see that x = 40. So 20% of the full 200ml potion is equal to 40ml of honey. Great, Richard can make the potion now. But wait – one more ingredient is still written in percent: Unicorn horn extract.
Percent Equation Example 2
17.5 percent of 200ml is what we are looking for. Let's use our formula again and subsitute: 17.5% for the percent, 200 for the whole, and x for the unknown part.
Once again we cross-multiply and get 100 · x = 17.5 times 200. We can simplify to 100x = 3500. Now we use opposite operations and divide both sides by 100. Doing so, we find that x = 35.
Therefore, Richard must use 35 ml of unicorn horn extract. Now he can finally make the potion to make the princess fall hopelessly in love with him... when suddenly (pooof)... And, well, Richard can't explain this very well but the racoon has started to look extremely beautiful to him.
Solving Percent Equations exercise
-
Describe how you can determine the percent of honey.
HintsDetermine which term is unknown. We know the quantity of love potion as well as the percent values.
Usually we use the letter $x$ for the unknown variable.
SolutionRichard has fallen in love with Princess Head Over Heals, but she doesn't like him one bit. So, using his grandmother's recipe, he wants to concoct a love potion.
The ingredients for $200~ml$ of love potion are:
- $20~\%$ honey,
- $\frac12$ batwing,
- $50$ teardrops of love and
- $17.5~\%$ horn of a unicorn.
We can use the equation $\frac{\text{part}}{\text{whole}}=\frac{\text{percent}}{100}$.
The whole amount shall be $200~ml$, and he needs $20$ percent of honey. First of all we plug in the known values as well as the variable $x$ for the unknown part and get: $\frac x{200}=\frac{20}{100}$.
We can use cross multiplication:
$100\times x =20\times 200$.
Simplifying leads to
$100x=4000$
and dividing by $100$ (opposite operation of multiplication) gives us the solution: Richard needs $40~ml$ of honey for his potion.
-
Calculate how much is $17.5~\%$ of $200~ml$.
HintsDecide what's the part, the whole, and percent.
The percent is given in the story above.
To make the recipe, we need unicorn horn extract and some other ingredients. Unicorn horn extract is a part of the potion, so it's quantity is a part of the whole quantity.
To cross multiply equal fractions or ratios, multiply the numerator of each side by the denominator of the other side and set the two products equal.
To isolate a variable use opposite operations:
- $+\longleftrightarrow -$ and
- $\times \longleftrightarrow \div$.
SolutionHow many $ml$ are in $17.5~\%$ of $200~ml$. This is the quantity of unicorn horn extract Richard needs to make the love potion.
Use the equation $\frac{\text{part}}{\text{whole}}=\frac{\text{percent}}{100}$.
The whole amount is $200~ml$, and the percent is $17.5$. Now we can substitute the part by $x$, the whole by $200$, and the percent by $17.5$ to get the following equation:
$\frac x{200}=\frac{17.5}{100}$.
Cross multiply to get: $100\times x =17.5\times 200$.
Simplifying give us: $100x=3500$.
Now we use the opposite operation of multiplication: division. We divide both sides by $100$ and get the result $x=35$. Richard needs $35~ml$ of unicorn horn extract to make the love potion.
-
Define the whole, the part, and the percentage.
HintsThe percentage can be $100$ at most.
The whole is the total quantity.
You can recognize percent by the $\%$ sign.
The whole is more than each part.
SolutionRemember the equation $\frac{\text{part}}{\text{whole}}=\frac{\text{percent}}{100}$.
It's very important to decide which part is the whole, which is the part and finally what the percentage is.
Let's take a look at the new recipe for the love potion.
- The total quantity $300$ is the whole.
- This whole is made up of different ingredients. If these are also given in $ml$ we talk about parts. So $60~ml$ honey is the part.
- We can recognize the percent by the $\%$ sign. So $40~\%$ unicorn horn extract is a percent.
- What is the whole? It's the total amount of $400$.
- And what are the parts? The parts are given in the same unit as the whole: $100~ml$ of bat ear extract and $120~ml$ of unicorn tears.
- You will finde the percentage by looking for the $\%$ sign: $20$ $\%$ of honey and $25$ $\%$ of milk.
-
Help Richard convert the percentage into $ml$.
HintsYou can add all the results. The sum is $200$.
The whole is the total quantity of the potion.
SolutionOh, all the ingredients are given in percent.
Richard is a little bit helpless. He needs to know exactly how many $ml$ he needs of each ingredient.
Convert the equation:
$\frac{\text{part}}{\text{whole}}=\frac{\text{percent}}{100}$
by cross multiplying:
$100\times x=\text{whole}\times \text{percent}$.
Dividing by $100$ will give Richard the information he needs:
$x=\text{whole}\times \text{percent}\div 100$.
- Dragon eye extract: $200\times 10\div100=20$ $ml$.
- Dragon tears: $200\times 30\div100=60$ $ml$.
- Eagle feather extract: $200\times 20\div100=40$ $ml$.
- Honey: $200\times 40\div100=80$ $ml$.
-
Explain the meaning of percent.
Hints$100$ cents equals one dollar.
One cent equals one hundredth of one dollar.
We can write percent as a decimal number: $20~\%=0.20$.
We can write a decimal number as percent by multiplying by $100$ and writing the $\%$ sign behind: $0.175=17.5~\%$.
SolutionRichard the mage needs $20~\%$ of honey and $17.5~\%$ unicorn horn extract to make the love potion. But what does this mean?
If the love potion is divided into $100$ equal parts then each part will represent one percent. Percent means one over hundred.
In this way $20~\%$ is the same as $20$ parts of the whole. So we have to divide by $100$ and multiply with $20$: $\frac{20}{100}=0.20$. You can also write: $100\times 0.20=20$. This is the number of parts of the potion.
In general we can use the equation $\frac{\text{part}}{\text{whole}}=\frac{\text{percent}}{100}$.
-
Determine the percentage.
HintsUse cross multiplication to solve for unknown quantities or check that the ratios are equal.
Find the percentage by multiplying $\large{\frac{\text{part}}{\text{whole}}}$ by $100$.
SolutionUsing the equation $\frac{\text{part}}{\text{whole}}=\frac{\text{percent}}{100}$.
We can either substitute the given values and transform this equation or transform this equation and substitute afterwards. This time the unknown is the percentage, so we assign the variable $x$ to the unknown value.
Cross multiplying leads to:
$100\times \text{part}=\text{whole}\times x$.
Now we divide by the whole and get:
$x=100 \times \text{part}\div \text{whole}$.
- $10$ parts of $100$ are $100\times 10\div 100=10~\%$.
- $100~ml$ of $400~ml$ are $100 \times 100 \div 400 = 25 ~\%$.
- $360$ miles in respect of $1200$ miles are $100 \times 360 \div 1200=30~\%$.
- $270~ml$ of $600~ml$ are $100 \times 270 \div 600=45~\%$.