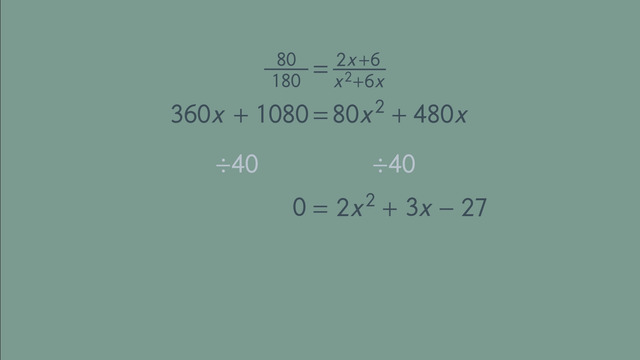Long Division of Polynomials
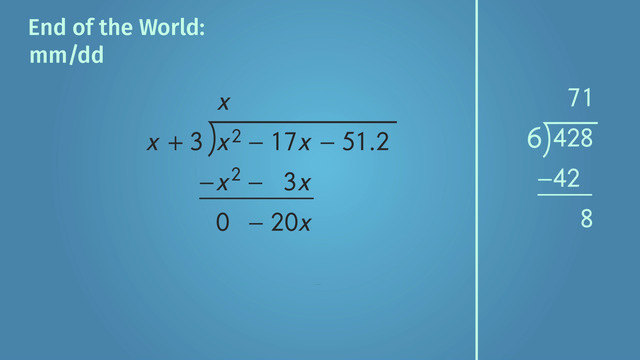

Basics on the topic Long Division of Polynomials
The procedure for performing long division with polynomials is very similar to the procedure for performing long division with real numbers. Learn how to execute this procedure by helping the scientists crack the code found in a message containing the date in which the world will end. Learning how to use long division with polynomials will give a better understanding of how to work with polynomials in general and give a sense for how polynomials behave in a similar fashion to real numbers. Common Core Reference: CCSS.MATH.CONTENT.HSA.APR.D.6.
Transcript Long Division of Polynomials
“The World --- will end on ---th 30--! No more --- for ---- of the year! ---” Scientists have intercepted a cryptic radio message and rush to save mankind. Luckily, the scientists’ robot was able to detect a code embedded in the message. The message is coded in math and tells them the exact day, month and year when the world will end. To solve the riddle and save the world, the scientists must use their knowledge of long division of polynomials.
The long division of polynomials
These are the equations the Robot overheard. The result of the first equation will tell us the month and date while the combined result of the next two equations will give us the year. Let's get started.
The first part of the message is the month and date: Long division with polynomials is no different than long division with numbers. Let's look at the easy example 428 divided by 6. In this example we first look at how many times 6 goes into 4. Since 6 does not go into 4 we have to look at the next digit. How many times does 6 go into 42. 6 goes into 42 7 times. Now multiply 7 times 6 which gives us 42. We subtract 42 from 42 and get zero. In the same way, we should ask ourselves, "How many times does 'x' go into x squared?" x' times 'x' gives us 'x' squared, so we write 'x'. Next, we multiply 'x' times 'x' plus 3. We subtract this result from the polynomial under the long division symbol. 'x' squared minus 'x' squared gives us zero. Negative 17x minus 3x gives us negative 20x.
Now, just like with regular long division, we bring the next number down and repeat the process of asking the question - How many times does the divisor go into the dividend? - until there are no numbers left. In this example, six goes into eight exactly one time. Then, we multiply 1 times 6 and get 6. This 6 is subtracted from the 8 and we're left with 2.
In the same way, we bring the negative 51.2 down to get the expression -20x - 51.2. Now we have to see how many times x goes into -20x. It goes in -20 times, which we write here. Then, we multiply -20 by 'x' plus 3 to get -20x minus 60. This is subtracted from the binomial negative 20x minus 51.2. This gives us 8.8.
What do we do with this? We know it's a remainder, but how do we know how many times 'x' goes into it?!? We don't even know what 'x' is! Don't worry, just like long division with numbers, you write the remaining numbers over the divisor. Normally, you have to simplify your fraction, if you can. But when your divisor has a variable, you can't simplify any further, so you're done! Remember, this remainder 8.8 tells us the month and date of the End of the world.
The second part of the message reveals the first two numbers of the year. Just like before, we ask, "how many times does 'x' go into 'x' squared?" We multiply our answer by our dividend, subtract and bring down the next term. We repeat the process. And finally, write the leftovers over our dividend, giving us the remainder. This remainder is the first 2 digits of the year the world will end. The scientists are almost done! Once they find out the last two digits of the year, they can save the world!
The third and final part of the message reveals the last two numbers of the year. Even though the scientists have to hurry, they stick to the plan and go step by step. * bring the next term down * multiply * subtract * and write the dividend over the divisor, and there you have it: the remainder!
So 1 and 6 are the last two digits of the year. With the code cracked, the scientists rush to enter the date into their time machine “8.8.3016”. That's strange, it sure doesn't look like the world's about to end. “The World Series will end on August 8th, 3016! No more games for the remainder of the year! Get your tickets now!.” Oh! Game 7 of the World Series!!!
Long Division of Polynomials exercise
-
Explain how to solve the equation using long division of polynomials.
HintsLong division with polynomials is a lot like regular long division.
Pay close attention to signs.
$x$ goes into $x^2$ $x$ times.
SolutionLong division with polynomials is a lot like regular long division.
You start by seeing how many times the first term of the divisor goes into the first term of the dividend. In this case, you find out how many times $x$ goes into $x^2$.
Next, you multiply the result by the divisor. You have that $x$ times $x+3$ gives us $x^2-3x$.
Then you subtract this result from the polynomial, as you can see in the image.
Then just like in regular long division, you bring down the next term in from the dividend. So here you bring $-51.2$ down.
The process above gets repeated, dividing the divisor into the result. So in this case you find out how many times $x$ goes into $-20x$. Then you multiply $-20$ by $x+3$. You subtract the result from the binomial $-20x -51.2$, giving you the remainder.
You divide the remainder $8.8$ by $x+3$ and add the result to binomial on top of the division sign.
-
Calculate the remainder using long division of polynomials.
HintsLong division with polynomials is a lot like regular long division.
Pay close attention to signs.
$x$ goes into $x^2$ $x$ times.
SolutionLong division with polynomials is a lot like regular long division.
You start by seeing how many times the first term of the divisor goes into the first term of the dividend. In this case, you find out how many times $x$ goes into $x^2$.
Next, you multiply the result by the divisor. $x$ times $x-11$ gives us $x^2-11x$.
Then you subtract this result from the polynomial, as you can see in the image.
Then just like in regular long division, you bring down the next term in from the dividend. So here you bring $115$ down.
The process above gets repeated, dividing the divisor into the result. So in this case you find out how many times $x$ goes into $-9x$. Then you multiply $-9$ by $x-11$. You subtract the result from the binomial $-9x +115$, giving you the remainder.
You divide the remainder $16$ by $x-11$ and add the result to binomial on top of the division sign.
-
Determine the result of each division operation.
HintsTry dividing the divisor into the dividend and seeing what result you get. You can do these calculations using long division with polynomials.
It may help to try doing the math without looking at the possible results.
SolutionYou can divide the divisor into the dividend and see what result you get. This will show you which result matches each dividend.
You can do this division using long division with polynomials.
Let's use the example of $\frac{x+5}{4x+16}$.
First, we see how many times $x$ goes into $4x$. The result is $4$.
Then, we multiply this result by the entire divisor. $4 \times (x+5)$ gives us $4x+20$. We subtract this result from the entire dividend, which gives us $-4$. Then $-4$ is the remainder.
We divide the remainder by the divisor, and add it to our solution. This gives us the overall result of $4-\frac{4}{x+5}$ from the long division.
So we can pair the dividend $4x+16$ with the result $4-\frac{4}{x+5}$.
Similarly,
The dividend $2x-12$ gives the result $2-\frac{22}{x+5}$.
The dividend $7x+35$ gives the result $7$.
The dividend $5x-19$ gives the result $5-\dfrac{44}{x+5}$.
-
Correct the calculations.
HintsThere are no mistakes in the divisor or the dividend.
There is one mistake in the final result.
There are two mistakes in the calculations that lead to the answer.
SolutionStart by seeing how many times the first term of the divisor goes into the first term of the dividend. In this case, you find out how many times $x$ goes into $x^2$. The result is $x$.
Next, you multiply the result by the divisor. $x$ times $x+3$ gives us $x^2+3x$.
Then you subtract this result from the polynomial; as you can see in the image, this gives you $0+4x$.
Then just like in regular long division, you bring down the next term from the dividend. So here you bring down $-8$.
The process above gets repeated, dividing the divisor into the result. So in this case you find out how many times $x$ goes into $4x$. Then you multiply $4$ by $x+3$. You subtract the result from the binomial $4x-8$, giving you the remainder.
You divide the remainder $20$ by $x+3$ and add the result to the binomial on top of the division sign.
-
Define the term "polynomial".
Hints$5x^2 + 3x -7$ is a polynomial.
Polynomials can have an infinite number of terms.
Although some terms in a polynomial are negative, they are all still being added together.
SolutionA polynomial is a type of algebraic expression. It must have two ore more terms. A binomial is a special kind of polynomial that has two terms.
The terms of a polynomial are added together and can be positive or negative. For example, you can think of the polynomial $5x^2 + 3x -7$ as "seven $x$ squared plus three $x$ plus negative seven".
The terms of a polynomial can contain both variables and constants. Using the above example, the term $5x^2$ contains both the variable $x$ and the constant $5$.
Polynomials can contain many variables. So the statement "Polynomials can only contain one variable" is false.
Any number of terms in a polynomial can be positive or negative. So the statement "More terms in a polynomial must be positive than negative" is false.
Polynomials can contain any number of terms. So the statement "Polynomials can contain up to five terms" is false.
-
Determine the result.
HintsTry doing the polynomial long division on paper.
The first step is to see how many times the first term of the divisor $x$ goes into the first term of the dividend $x^4$.
The second step is to subtract $x^3(x+2)$ from the first two terms of the dividend, and bring down the next term in the dividend ($-15x^2$) next to the result.
The middle steps of polynomial long division get repeated, just like in regular long division.
SolutionThe first step is to see how many times the first term of the divisor $x$ goes into the first term of the dividend $x^4$. The result is $x^3$.
The second step is to subtract $x^3(x+2)$ from the first two terms of the dividend, and bring down the next term in the dividend, $-15x^2$, next to the result.
The third step is to see how many times the first term of the divisor $x$ goes into the first term of the result from the second step, $-16x^3-15x^2$. The result is $-16x^2$.
The second and third steps get repeated over and over, until the last term in the dividend is reached. At this point, the remainder, $50$, is found, and divided by the divisor to get the last term in the solution.