Introduction to Simultaneous Linear Equations

Basics on the topic Introduction to Simultaneous Linear Equations
After this lesson, you will be able to analyze and solve simultaneous linear equations.
The lesson begins by teaching you that a linear equation only has variables raised to the first power. It leads you to learn that simultaneous linear equations can be graphed in on one Cartesian plane. It concludes by showing you that the intersection of the graph of two simultaneous linear equations determines their common solution.
Learn about simultaneous linear equations by helping Thomas and Dieter calculate their monthly sales.
This video includes key concepts, notation, and vocabulary such as linear equation (equation with only variables raised to the first power); simultaneous equations (equations which happen at the same time and can be graphed on the same Cartesian plane); simultaneous solution (a solution to simultaneous equations); and coordinate plane (a plane formed by horizontal and vertical lines called the x- and y-axis).
Before watching this video, you should already be familiar with substitution, point-plotting, and graphing and writing linear equations using variables.
After watching this video, you will be prepared to learn how to solve systems of linear equations algebraically, find solutions by graphing equations, and solve real-world and mathematical problems that use two linear equations in two variables.
Common Core Standard(s) in focus: 8.EE.C.8 A video intended for math students in the 8th grade Recommended for students who are 13-14 years old
Transcript Introduction to Simultaneous Linear Equations
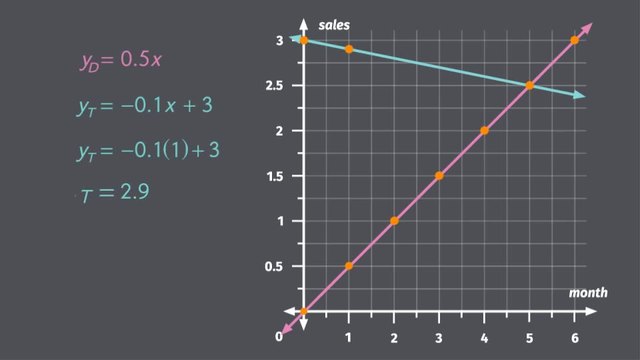
Fans of the beloved 80's pop duo, Vintage Silence, were shocked and saddened when the band broke up. Rumor was, they were experiencing some "creative differences". Thomas wanted to take his music in a more digital direction and Dieter wanted to unplug and focus on songwriting. But they were so great together! How will they ever make it on their own? Maybe we can find out by investigating Simultaneous Linear Equations. After breaking up, Dieter and Thomas both released solo records in the same month. Let's see how they're doing. This table shows Dieter's monthly record sales, in millions, for the first five months after his album is released. In the first month, he sold half a million records and in the second month, he sold one million! In fact, every month he sells half a million records more than he did the previous month. That means we can write this as a linear equation using variables! Since the amount of records sold depends on the month we can call the number of the month 'x' and the number of records sold that month, 'y'. Because Dieter's monthly sales are increasing by one half million each month, we can write 'y' is equal to zero point five times the month, 'x'. Notice both the variables are raised to the first power. So this must be a linear equation. Let's put this on a coordinate graph by starting at the origin then going up by half a million each month. Notice that all of the points in our table are also points on this graph. But what about Thomas? We don't have a table for his sales, we just have this equation. Since both of the variables are raised to the first power, we know this is a linear equation. So we can graph it with substitution, then by connecting the points with a line. If we plug in 0 for x we see that the number of record sales will be 3 million. Interesting, I guess he must have had some pre-sales. To find out how many records he sold in the first month, we just plug in 1 for 'x' then we get...2.9 for y? Oh no! It looks like his monthly sales decreased by 0.1 million! That's not a good sign for his solo career. By looking at the graph, we can notice a couple things. Because they are selling records at the same time, we are able to graph these on the same coordinate plane. This means they are Simultaneous Equations. Also notice that in month five, both Dieter and Thomas sell two and a half million records. When two graphs intersect like this, it means they have a simultaneous solution. The solution in this graph is the point where the month and the number of records sales are the same for both equations. Simultaneous equations are often written like this: Notice that a bracket is used to show that the two equations are happening simultaneously. We can use substitution to check the solution we found on our graph. Just plug in the coordinates for the solution into both equations. So if we set 'x' equal to 5, and 'y' equal to 2.5 in Dieter's equation... We end up with 2.5 equals 2.5.. This is a true statement, so this point works as a solution for Dieter. Now, let's check and verify that this is also a solution for Thomas. Using the same point, we set 'x' equal to 5 and 'y' equal to 2.5 in Thomas's equation and we end up with the true statement 2.5 equals 2.5. One point works for both equations, so this means we definitely have a simultaneous solution. To review: Simultaneous linear equations are equations that happen at the same time. So, you graph them on the same coordinate plane and see their solution at the point of intersection. You can check the solution algebraically with substitution. But what does all this mean for Vintage Silence? Not only are Thomas's album sales tanking but nobody turned up for his concert except for one person. No way... Is that...? I can't believe it! They're finally back together! Aww, who needs fans and fame when you have each other?
Introduction to Simultaneous Linear Equations exercise
-
Pair the graphs of the simultaneous linear equations with their intersection point.
Hints- Simultaneous equations are a set of two or more equations, each containing two or more variables whose values can simultaneously satisfy both or all the equations in the set.
- The point of intersection is the solution that works for both equations.
The intersection point is an ordered pair $(x,y)$.
- The $x$-value is represented along the horizontal axis
- The $y$ value is represented along the vertical axis
For the two simultaneous equations, the point of intersection is $(-4,-2)$.
SolutionThe intersection point for each graph is an ordered pair $(x,y)$.
- The $x$-value is represented by the horizontal axis
- The $y$ value is represented by the vertical axis
The ordered pair $(1,-1)$ is the intersection points for the green lines.
The ordered pair $(0,-2)$ is the intersection points for the red lines.
The ordered pair $(2,2)$ is the intersection points for the blue lines.
The ordered pair $(4,6)$ is the intersection points for the purple lines.
The ordered pair $(-6,2)$ is the intersection points for the yellow lines.
-
Determine the intersection point given a table and equation.
HintsTo find the point of intersection, graph the coordinates given in the table and the equation of the line.
Slope-intercept form, $y=mx+b$, where $m$ is the slope and $b$ is the y-intercept, is one way to graph a line. Another way is to substitute $x$-values into the equation and solve for $y$, then plot the ordered pairs.
Graph the coordinates from the table for equation 1 and the horizontal line, $y=3$. You will see that the intersection point is $(1,3)$.
Graph the coordinates from the table for equation 1 and the line, $y=-\frac{1}{2}x-1$. You will see that the intersection point is $(-2,0)$.
SolutionTo find the intersection point using a table and an equation, graph the simultaneous equations and identify the coordinates of the simultaneous solution (point of intersection).
Remember to graph a linear equation you can use the slope-intercept form, $y=mx+b$, where $m$ is the slope and $b$ is the $y$-intercept, or find ordered pairs $(x,y)$ by substituting values for $x$ and solving for $y$.
1. The intersection point for the simultaneous equations on a coordinate plane is $(-1, -1)$.
2. The intersection point for the simultaneous equations on a coordinate plane is $(-1.5, -3)$.
3. Since equation $y=2$ is the horizontal line at $y=2$, we know the $y$-coordinate for the simultaneous solution has to be 2. You can graph the two lines to find the point of intersection is $(-2, 2)$.
4. The intersection point for the simultaneous equations on a coordinate plane is $(0,0)$.
-
Identify the graphs of the simultaneous equations.
HintsSimultaneous equations have a solution. The solution is found by identifying the point of intersection where both lines have the same values.
One way to identify the graph of a set of equations is by graphing the equations using the point-slope form, $y=mx+b$, where $m$ is the slope and $b$ is the $y$-intercept.
Another way to identify the graph of a set of equations is to substitute the intersection point, $(x,y)$, into both equations. If the simplified expressions are true, then $(x,y)$ is intersection point and solution to both equations.
SolutionOne way to identify the graph of a set of equations is by graphing the equations using the point-slope form, $y=mx+b$, where $m$ is the slope and $b$ is the $y$-intercept.
Another way to identify the graph of a set of equations is to substitute the intersection point, $(x,y)$, into both equations. If the simplified expressions are true, then $(x,y)$ is intersection point and solution to both equations.
1. The graph with green lines that intersect at $(2,1)$ matches with the set, $\left\{\begin{matrix} y=\frac{1}{2}x\\ y=-x+3 \end{matrix}\right.$
Check that the intersection point $(2,1)$ satisfies both equations:
- In the equation, $y=\frac{1}{2}x$, $1=\frac{1}{2}(2)$, $1=1$.
- In the equation, $y=-x+3$, $1=-2+3$, $1=1$.
Check that the intersection point $(-4,4)$ satisfies both equations:
- In the equation, $y=-\frac{3}{4}x+1$, $4=-\frac{3}{4}(-4)+1$, $4=3+1$, $4=4$.
- In the equation, $y=\frac{1}{2}x+6$, $4=\frac{1}{2}(-4)+6$, $4=-2+6$, $4=4$.
Check that the intersection point $(-4,3)$ satisfies both equations:
- In the equation, $y=3$, $3=3$.
- In the equation, $y=\frac{3}{2}x+9$, $3=\frac{3}{2}(-4)+9$, $3=-6+9$, $3=3$.
Check that the intersection point $(3,3)$ satisfies both equations:
- In the equation, $x=3$, $3=3$.
- In the equation, $y=\frac{3}{5}x+\frac{6}{5}$, $3=\frac{3}{5}(3)+\frac{6}{5}$, $3=3$.
-
Find the intersection point of the lines.
HintsThe intersection point is where the two lines meet. This can be found by graphing. Three specific ways you may have learned how to graph are:
1. Finding the $x$ and $y$ intercepts.
2. Using point-slope form, $y=mx+b$.
3. Finding ordered pairs $(x,y)$. (This is also a part of creating a table.)
To graph the equation, $y=2x+4$, using point-slope form, $y=mx+b$,
1. Identify the slope, $m=2$ or $m=\frac{2}{1}$.
2. Identify the $y$-intercept, $b=4$.
3. Graph the $y$-intercept, $(0,4)$.
4. Use the slope, $m=2$ or $m=\frac{2}{1}$, to graph a second point start at the $y$-intercept, rise 2, then move right 1.
To graph ordered pairs for the equation $y=2x+4$, choose two values to substitute for $x$, and solve for $y$. Graph the two points then draw a line from one point to the other.
- Let $x=0$, then $y=2(0)+4=4$. The ordered pair is $(0,4)$.
- Let $x=1$, then $y=2(1)+4=5$. The ordered pairs is $(1,5)$.
SolutionTo find the intersection point for the simultaneous equations, graph the equations by using one of the following methods, then you can visually identify the point of intersection.
1. Finding the $x$ and $y$ intercepts.
2. Using point-slope form, $y=mx+b$.
3. Finding ordered pairs $(x,y)$.
The graph shows the solution for the first set of equations, $\left\{\begin{matrix} y=2x+3\\ y=-2x-5 \end{matrix}\right.$
Below is an explanation on how to graph the first set of equations by finding ordered pairs. You may follow this method or choose another method to graph the other simultaneous equations.
1. $\left\{\begin{matrix} y=2x+3\\ y=-2x-5 \end{matrix}\right.$
- To graph the lines, find two ordered pairs by choosing random values for $x$ and solving for $y$.
- For the line $y=2x+3$, when $x=1$, $y=5$ and when $x=0$, $y=3$. Graph the points $(1,5)$ and $(0,3)$ then draw a line.
- For the line $y=-2x-5$, when $x=-1$, $y=-3$ and when $x=0$, $y=-5$. Graph the points $(-1,-3)$ and $(0,-5)$ then draw a line.
- From the graph you will see that the intersection point is $(-2,-1)$
- Use substitution to check the solution $(-2, -1)$. If the left side of the equation equals the right side of the equation, we can conclude that the solution is correct.
- In the equation $y=2x+3$, $-1=2(-2)+3$ simplifies to $-1=-1$.
- In the equation $y=-2x-5$, $-1=-2(-2)-5$ simplifies to $-1=-1$.
- From the graph you will see that the intersection point is $(0,3)$
- Use substitution to check the solution $(0, 3)$.
- In the equation $y=\frac{1}{2}x+3$, $3=\frac{1}{2}(0)+3$ simplifies to $3=3$.
- In the equation $y=-3x+3$, $3=-3(3)+3$ simplifies to $3=3$.
- From the graph you will see that the intersection point is $(3,3)$
- Use substitution to check the solution $(3, 3)$.
- In the equation $y=-x+6$, $3=-3+6$ simplifies to $3=3$.
- In the equation $y=x$,$3=3$.
- From the graph you will see that the intersection point is $(-2.5,4)$
- Use substitution to check the solution $(-2.5, 4)$.
- In the equation $y=-\frac{3}{2}x+\frac{1}{4}$, $4=-\frac{3}{2}(-2.5)+\frac{1}{4}$ simplifies to $4=4$.
- In the equation $y=2x+9$, $4=2(2.5)+9$ simplifies to $4=4$.
-
Use the table to graph points and the line.
HintsA point on a graph consists of an $x$-value and a $y$-value. In a table, if $x$ is $1$ and $y$ is $2$, the point is $(1,2)$.
To graph the ordered pair, $(1,2)$, start at the origin $(0,0)$ and move $1$ unit to right on the $x$-axis then 2 units up on the $y$-axis.
If the ordered pair is $(-1,-2)$, start at the origin $(0,0)$, and move 1 unit to the left on the $x$-axis then $2$ units down on the $y$-axis.
SolutionThe image shows the points plotted from the table and the line going through the points.
The graph we were given didn't allow us to highlight points $(0,3)$ and $(2, -1)$ but they are still there as represented by the continuous line.
A point on a graph consists of an $x$-value and $y$-value.
To graph the ordered pair, $(x,y)$, move $x$ units on the $x$-axis then $y$ units on the $y$-axis.
If $x$ is positive, the point will move to the right, and if $x$ is negative the point will move to the left.
If $y$ is positive, the point will move up, and if $y$ is negative the point will move down.
-
Determine if the two linear equations intersect or not.
HintsParallel lines are always the same distance apart and never touch.
To see if the lines intersect, use one of the following methods to graph the equations:
1. Find and graph the $x$ and $y$ intercepts. 2. Find the $y$-intercept and slope using point-slope form, $y=mx+b$. 3. Find and graph ordered pairs $(x,y)$.
1. $\left\{\begin{matrix} y=3x+1\\ y=3x-3 \end{matrix}\right.$
These equations are parallel which means they do not intersect.
2. $\left\{\begin{matrix} y=-5x+1\\ y=5x-3 \end{matrix}\right.$
These equations intersect.
SolutionGraph the equations by using either point-slope form, $y=mx+b$, where $m$ is the slope and $b$ is the y-intercept, finding the $x$ and $y$ intercepts, or by graphing ordered pairs $(x,y)$.
The graph shows the solution for the first set of equations, $\left\{\begin{matrix} y=3x-1\\ y=2x \end{matrix}\right.$
Below is an explanation on how to graph the first set of equations by finding ordered pairs. You may follow this method or choose another method to graph the other simultaneous equations.
1. $\left\{\begin{matrix} y=3x-1\\ y=2x \end{matrix}\right.$
- To graph the lines, find two ordered pairs by choosing random values for $x$ and solving for $y$.
- For the line $y=3x-1$, when $x=2$, $y=5$ and when $x=0$, $y=-1$. Graph the points $(2,5)$ and $(0,-1)$ then draw a line.
- For the line $y=2x$, when $x=2$, $y=4$ and when $x=0$, $y=0$. Graph the points $(2,4)$ and $(0,0)$ then draw a line.
- A graph of the simultaneous equations will show the intersection point, $(1,2)$.
- A graph of the simultaneous equations will show the intersection point, $(0,-1)$.
- A graph of the equations will show that the lines are parallel. This means that they do not intersect.
- A graph of the simultaneous equations will show the intersection point, $(6,4)$.
- A graph of the equations will show that the lines are parallel. This means that they do not intersect.