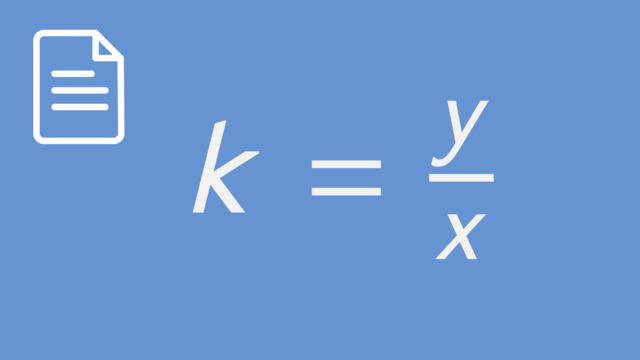Identifying Negative Proportional Relationships in Graphs

Basics on the topic Identifying Negative Proportional Relationships in Graphs
After this lesson, you will be able to confirm negative proportional relationships in graphs.
The lesson begins by teaching you that the slope of a negative proportional relationship is negative. It leads you to learn that since it is linear relationship, the graph is a straight line. It concludes by emphasizing that the graph should pass through the origin.
Learn about negative proportional relationships in graphs by helping Professor Penguin train Wheezy, Macaroni, and Pipsqueak in diving.
This video includes key concepts, notation, and vocabulary such as negative slope (which means as the x-value increases, the corresponding y-value decreases), linear relationship (slope is the same as the rate of change or constant of proportionality for any two points on the line), and the application of the zero property (graphs of proportional relationships should pass through the origin since multiplying the zero x value by any constant of proportionality yields a zero y value)
Before watching this video, you should already be familiar with slope, equivalent ratios, constant of proportionality and linear relationships.
After watching this video, you will be prepared to identify and compute negative constants of proportionality that can be used in equations aimed at solving real-world problems.
Common Core Standard(s) in focus: 7.RP.A.2.A A video intended for math students in the 7th grade Recommended for students who are 12 - 13 years old
Transcript Identifying Negative Proportional Relationships in Graphs
Somewhere in the frozen wasteland of Antarctica, three brothers, Wheezy, Macaroni, and Pipsqueak, are enrolling in Professor Penguin's Diving School. Their goal? To overcome their fear and learn to dive like pros! To judge their proficiency, Professor Penguin will compare their diving techniques to negative proportional relationships in graphs. At their group lesson, Wheezy, Macaroni, and Pipsqueak will each take a turn diving into the icy depths. Professor Penguin will analyze their technique by comparing their dives to the graphs of negative proportional relationships because, in the Professor's opinion, this kind of graph also represents the IDEAL penguin diving form. Let's break down what we know about these graphs. First of all, the slope of a negative proportional relationship is, well, negative. That means as 'x' increases and goes to the right, 'y' decreases and goes down. Next, negative proportional relationships are linear. Linear means that the slope, or rate of change, always stays the same. That's why their graphs look like straight lines. Finally, in a negative proportional relationship, all points on the graph represent equivalent ratios. That means in order to find any y-value on the graph, you can take your constant of proportionality, 'k', also known as the slope, and multiply it by the corresponding x-value. Because this is a proportional relationship, when 'x' equals zero, 'y' must also equal zero. Because zero times any value is zero. This is why a negative proportional relationship must pass through the origin, or the point (0, 0). Let's check in with the penguin brothers to see how their diving lesson is going. Wheezy is the oldest brother, so he's up first! He sneakily starts at 2 feet below the surface. That's a depth of negative two feet when his horizontal distance is zero. Professor Penguin blows his whistle and Wheezy is off! He's looking good as he passes through the point (1, -3). A moment later, he's at point (2, -4). He keeps up this rate, diving one foot deeper for each foot he swims out. Is Wheezy's dive a negative proportional relationship? Well, Wheezy's line has a negative slope, because as 'x' increases 'y' decreases, and Wheezy's progress is definitely linear, because his dive is in a straight line. But is Wheezy's progress proportional? Hmm, his line doesn't pass through the origin. That's because he sneakily tried to get a head start on his brothers. So although Wheezy's progress is linear and negative, it's not proportional. He probably shouldn't expect very good marks from Professor Penguin. Let's look in on Macaroni, the middle brother. Macaroni waits on the side of the pool until Professor Penguin blows his whistle. At the very same instant, he dives! That's a great start by Macaroni, as he passes through the point (1, -2)! His form is looking solid, as he continues past point (2, -4), and he keeps going, descending an additional 2 feet down for every one foot he swims out horizontally! Based on what you know about negative proportional relationships, how will Professor Penguin judge Macaroni's dive? Well, the slope is negative, because Macaroni is going deeper and deeper as he dives. Also, his diving rate is consistent at negative two feet for every horizontal foot he swims out, so just like Wheezy, his graph is a straight line. But because he started at (0, 0), his line also passes through the origin. A straight line, going down, passing through the origin! That makes this dive a textbook negative proportional relationship. Now comes the youngest, Pipsqueak, sporting some stylish inflatable swimmies. Pipsqueak calms his nerves, waits for the Professor's whistle, then jumps into the water! After passing the one foot mark he is at a depth of zero feet. After swimming out two feet he dives to a depth of zero feet. It seems like he's going to keep going at this rate, but wait! After the three-foot mark he starts to descend. It looks like his swimmies have sprung a leak and he's sinking like a stone! Let's take this opportunity to figure out if Pipsqueak's unusual training graph represents a negative proportional relationship. Well it does go down at the end, but does it have a negative slope at the beginning? And his dive starts out as a straight line, but what happens around the three-foot mark? One thing we can say is that his graph does go through the origin. But is that enough to make Pipsqueak's dive a negative proportional relationship? No, because this graph is not a straight line and it does not have a negative slope. Better luck next time, Pipsqueak. Let's review what we've learned about the graphs of negative proportional relationships. Negative proportional relationships are special types of linear relationships. Because their slopes are negative, the x-value increases and goes to the right as the y-value decreases and goes down. And because these relationships are linear, their graphs are straight lines. Finally, because these are graphs of proportional relationships, they must pass through the origin. Oh, excuse us, I guess the diving lesson isn't quite over yet. Where are you paddling off to, Pipsqueak? Ah, I guess he got lost. Anybody want to join?