FOILing and Explanation for FOIL
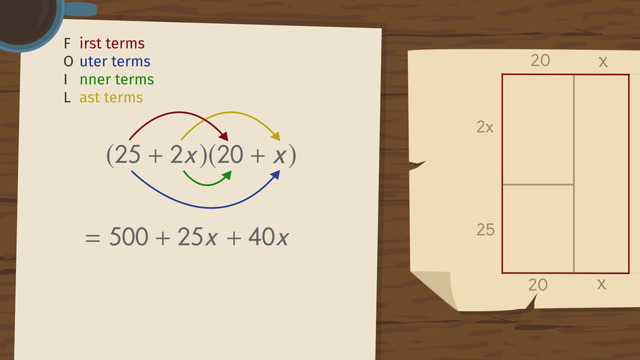

Basics on the topic FOILing and Explanation for FOIL
One way of getting the product of two binomials is the FOIL method. The term “FOIL” represents the position of the terms of the binomials; i.e. It is an acronym for “First-Outer-Inner-Last”.
Using the FOIL method means performing the following steps: 1. Take the product of each pair of terms of the binomials - the first, outer, inner, and last terms. 2. Simplify the product by combining existing like terms. 3. Arrange the terms of the product in descending order according to their degree.
More specifically, if we want to multiply two binomials, like (a+b) and (c+d), then we multiply the first terms of each binomial, ac, then we multiple the outer two terms, ad, then the inner two terms, bc, and finally the last two terms, bd. Then we add these products together to get that
(a+b)(c+d)=ac+ad+bc+bd,
making sure that we simplify by combining like terms, and rearrange terms from highest to lowest degree (by convention).
The FOIL method is an essential tool, as it is needed in any instance involving multiplying polynomials.
Perform arithmetic operations on polynomials.
CCSS.MATH.CONTENT.HSA.APR.A.1
Transcript FOILing and Explanation for FOIL
John Dolittler comes home from work and reads his mail. One letter catches his interest. It's a letter from a distant aunt. What's this? The letter says that he will inherit all of her money and all of her beloved animals from all over the world. John really loves animals, and has always wanted to have a little zoo. This is his big chance! Animals needs space, but that shouldn't be a problem with his new-found fortune. To help with his planning, John will use the FOIL method.
Multiplying two binomials
John finds an old map of his property and the nearby fields. But over time, the measurements of the fields have faded on the map. John knows that his property is 25 meters by 20 meters. He can't read the width of the field next to his property so he writes 'x' for its width. He also knows that the field above his property has a length that is twice as long as the other property's width, so it can be represented by 2x. If John buys both of these fields, the length of his new property would be 25 + 2x and the width would be 20 + x. For the total area, he multiplies these expressions by using the FOIL method. FOIL is an easy way to remember how to multiply two binomials.
The 'F' in FOIL stands for First, this means that you should multiply the two numbers that come first in each parentheses, 25 times 20 is 500. The 'O' stands for Outer, this means that you should multiply the two numbers on the outside. 25 times 'x' is 25x. The 'I' stands for Inner, the two inner numbers 2x times 20 make 40x. The 'L' stands for Last. You should multiply the numbers that come last in each set of parentheses. 2x times x is 2x squared.
After combining like terms and rearranging the terms in order of degree, we get 2x squared + 65x + 500. But FOIL only works when you are multiplying two binomials. So, why does it work anyway?
When we use the FOIL method, we are really just using the Distributive Property. The overall goal is to multiply every term in the first set of parentheses by every term in the second set of parentheses. We can do this by using the Distributive Property twice. Our first 'a' is the quantity 25 plus 2x, our first 'b' is 20 and our first 'c' is 'x'. Distributing the quantity 25 plus 2x over the quantity 20 plus 'x' gives us the following. Now, let's rearrange our equation to look like the definition of the distributive property.
What comes next? You guessed it! The distributive property comes to the rescue once again! 20 times 25 is 500. 20 times 2x is 40x. 'x' times 25 is 25x. 'x' times '2x' is 2x squared. After combining like terms and rearranging the terms by decreasing degree, we get 2x squared + 65x + 500. As you can see, it is the same as the FOIL method. But using FOIL cuts out a couple of steps.
Distributive Property
John isn't sure the area is big enough, so he's thinking about buying a third field. He knows that this field is three times as wide as the field next to his property. To calculate the bigger area, he rewrites the expression (25 + 2x) times (20 +x+3x). Since the FOIL method only works for multiplying two binomials, John has to use the Distributive Property. John breaks it up into three problems.
First, he multiplies (25 + 2x) by 20, then by x, and at last by 3x. By using the Distributive Property here, we get the following: 25 times 20 is 500, 2x times 20 is 40x, 25 times 'x' is 25x, 2x times 'x' is 2x squared, 25 times 3x equals 75x and 2x times 3x is 6x squared. After combining like terms, the area is 8x squared + 140x + 500. Don't forget to write the terms in order of decreasing degree. But careful, sometimes you can simplify first. Since 'x' and 3x are like terms, John could have combined them to get (20 + 4x) in the second parentheses.
Now we can use the FOIL method because it's the product of two binomials.
- First: 25 times 20 is 500.
- Outer: 25 times 4x is 100x.
- Inner: 2x times 20 is 40x.
- Last: 2x times 4x is 8x squared.
Look how big the new plot will be! John decides to buy the whole area for his little zoo.
John is just finishing up the zoo when the animals arrive. He's so excited that he can't wait to see what animals his aunt has collected from all over the world. What is this? Well, John tries to make the most out of his situation.
FOILing and Explanation for FOIL exercise
-
Calculate $(25 + 2x)(20 + x)$ using the FOIL method.
HintsFOIL is an easy way to remember how to multiply two binomials:
F first multiply the first terms.
O next multiply the outer terms.
I now the inner terms.
L last multiply the last terms.
$25$ and $20$ are the first terms of the two binomials.
Here you see an example using the FOIL method.
SolutionFOIL is an easy way to remember how to multiply two binomials.
F stands for first, meaning multiply the first terms $25\times 20=500$.
O stands for outer, meaning multiply the outer terms $25\times x=25x$.
I stands for inner, meaning multiply the inner terms $2x\times 20=40x$.
L stands for last, meaning multiply the last terms $2x\times x=2x^2$.
But the calculation isn't finished yet! We still have to combine the like terms and arrange the terms such that the resulting polynomial starts with the highest degree term and ends with the lowest one:
$(25+2x)(20+x)=500+25x+40x+2x^2=500+65x+2x^2=2x^2+65x+500$.
-
Determine the area of the zoo via the distributive property and the FOIL method.
HintsThe FOIL method only works for the multiplication of two binomials.
The distributive property is $a(b\pm c)=ab\pm ac$.
Remember to combine like terms. For example, $3x+5x=8x$.
SolutionThe total area of the fields on the old map can be represented as the product $(25+2x)(20+x+3x)$.
The second term is a trinomial, not a binomial, so the FOIL method cannot be applied. But we can use the distributive property, $a(b\pm c)=ab\pm ac$, to get
$(25+2x)(30+x+3x)=(25+2x)(20)+(25+2x)(x)+(25+2x)(3x)$.
We use the distributive property once again to get
$(25+2x)(20)+(25+2x)(x)+(25+2x)(3x)=500+40x+25x+2x^2+75x+6x^2$.
Next we combine like terms:
$500+40x+25x+2x^2+75x+6x^2=500+140x+8x^2$,
and rearrange the powers according to the degree,
$500+140x+8x^2=8x^2+140x+500$.
We could have also combined like terms in $20+x+3x$ to get $20+4x$. Then we are multiplying two binomials, $(25+2x)(20+4x)$, and we can use the FOIL method:
- F multiply the first terms $25\times 20=500$.
- O multiply the outer terms $25\times 4x=100x$.
- I multiply the inner terms $2x\times 20=40x$.
- L multiply the last terms $2x\times 4x=8x^2$.
$(25+2x)(20+4x)=500+100x+40x+8x^2=500+140x+8x^2=8x^2+140x+500$.
We can now see that with either method, we get the same result in the end. And John now knows the total area of the fields on the old map and can start planning the construction of his dream zoo!
-
Identify the right formula for calculating the area.
HintsFirst establish the multiplication.
For example the leftmost one is $(30+3x)(45+x)$.
Next combine like terms if there are any.
You can use the FOIL method for all these examples.
F stands for multiply the first terms.
O stands for multiply the outer terms.
I stands for multiply the inner terms.
L stands for multiply the last terms.
SolutionFor calculating the regarding areas we use the FOIL method
F multiply the first terms.
O multiply the outer terms.
I multiply the inner terms.
L multiply the last terms.
$~$
For the leftmost one we have:
$(30+3x)(45+x)$
- F $30\times 45=1350$
- O $30\times x=30x$
- I $3x\times 45=135x$
- L $3x\times x=3x^2$
$(30+3x)(45+x)=1350+30x+135x+3x^2=1350+165x+3x^2=3x^2+165x+1350$.
$~$
For the next example we first simplify the second factor, and then use the FOIL method:
$(30+3x)(45+x+2x)=(30+3x)(45+3x)$
- F $30\times 45=1350$
- O $30\times 3x=90x$
- I $3x\times 45=135x$
- L $3x\times 3x=9x^2$
$(30+3x)(45+3x)=1350+90x+135x+9x^2=1350+225x+9x^2=9x^2+225x+1350$.
$~$
For the next, we have:
$(40+2x)(15+4x)$
- F $40\times 15=600$
- O $40\times 4x=160x$
- I $2x\times 15=30x$
- L $2x\times 4x=8x^2$
$(40+2x)(15+4x)=600+160x+30x+8x^2=600+190x+8x^2=8x^2+190x+600$.
$~$
For the rightmost one, we first have to simplify one factor before using the FOIL method:
$(40+2x)(15+4x+10+2x)=(40+2x)(25+6x)$
- F $40\times 25=1000$
- O $40\times 6x=240x$
- I $2x\times 25=50x$
- L $2x\times 6x=12x^2$
$(40+2x)(15+4x)=1000+240x+50x+12x^2=1000+290x+12x^2=12x^2+290x+1000$.
-
Calculate the new area of the zoo.
HintsCombine the like terms in order to use the FOIL method.
You have to calculate the product $(25+2x)(20+6x)$.
Here is an example using the FOIL method, combining like terms, and rearranging the powers.
SolutionTo calculate the total needed area for John's Zoo we have to multiply the length $25+2x$ with the width $20+x+3x+2x$.
To use the FOIL method we first have to simplify the width term to $20+6x$.
Now we have to calculate $(25+2x)(20+6x)$:
- F $25\times 20=500$
- O $25\times 6x=150x$
- I $2x\times 20=40x$
- L $2x\times 6x=12x^2$
$(25+2x)(20+6x)=500+150x+40x+12x^2=500+190x+12x^2=12x^2+190x+500$.
-
Decide when the FOIL method can be used.
HintsF stands for multiply the first terms.
O stands for multiply the outer terms
I stands for multiply the inner terms.
L stands for multiply the last terms.
A binomial is the result of adding or subtracting two monomials. For example:
- $2x$ and $3$ are monomials.
- $2x+3$ is a binomial.
A trinomial is the result of adding or subtracting three monomials.
SolutionFOIL is an easy way to remember how to multiply two binomials.
And it only works when you are multiplying two binomials.
F stands for multiply the first terms.
O stands for multiply the outer terms
I stands for multiply the inner terms.
L stands for multiply the last terms.
-
Find the mistakes in the calculations.
HintsYou can use the FOIL method also for differences.
Pay attention to the sign.
Consider this example:
$\begin{array}{rcl} (1+x)(3-x)&=&~1\times 3+1\times (-x)+x\times 3+x\times (-x)\\ &=&~3-x+3x-x^2 \end{array}$
If necessary, first simplify the terms.
There are ten mistakes in total.
SolutionRemember the following:
- For using the FOIL method we have to simplify the factors if necessary.
- You can also use the FOIL method for differences. But you have to pay attention to the sign.
$\begin{array}{rcl} (15-x)(20+3x)&=&~15\times 20+15\times 3x+(-x)\times 20+(-x)\times 3x\\ &=&~300+45x-20x-3x^2\\ &=&~300+25x-3x^2\\ &=&~-3x^2+25x+300 \end{array}$
$\begin{array}{rcl} (25-2x)(40-2x)&=&~25\times 40+25\times (-2x)+(-2x)\times 40+(-2x)\times (-2x)\\ &=&~1000-50x-80x+4x^2\\ &=&~1000-130x+4x^2\\ &=&~4x^2-130x+1000 \end{array}$
Lastly we still have a multiplication where we first have to simplify both factors: $(25+2x-4x)(20+3x-10-7x)=(25-2x)(10-4x)$.
$\begin{array}{rcl} (25-2x)(10-4x)&=&~25\times 10+25\times (-4x)+(-2x)\times 10+(-2x)\times (-4x)\\ &=&~250-100x-20x+8x^2\\ &=&~250-120x+8x^2\\ &=&~8x^2-120x+250 \end{array}$
What are Quadratic Functions?
Graphing Quadratic Functions
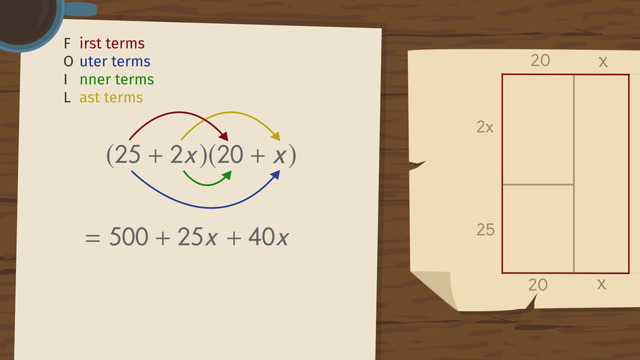
FOILing and Explanation for FOIL

Solving Quadratic Equations by Taking Square Roots
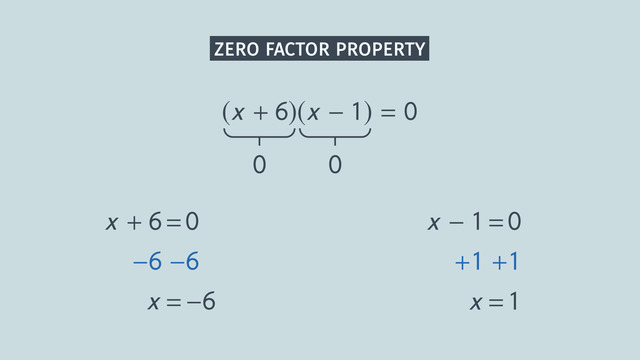
Solving Quadratic Equations by Factoring
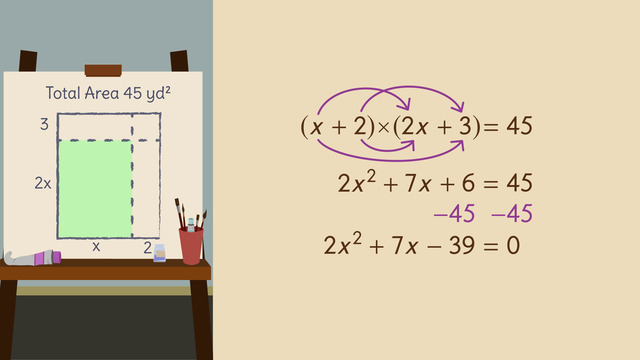
Factoring with Grouping

Solving Quadratic Equations Using the Quadratic Formula

Solving Quadratic Equations by Completing the Square
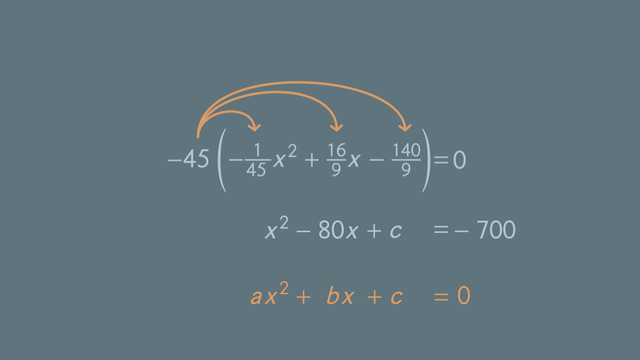
Finding the Value that Completes the Square
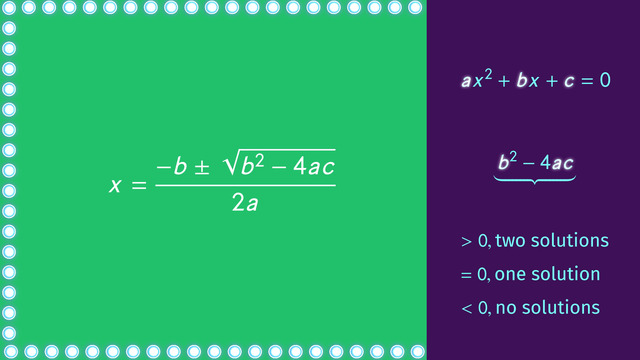
Using and Understanding the Discriminant
Word Problems with Quadratic Equations











