Finding the Value that Completes the Square
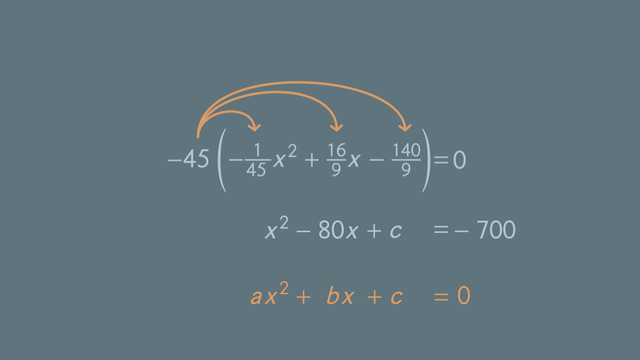

Basics on the topic Finding the Value that Completes the Square
Quadratic equations can be solved by using a certain method known as “completing the square”.
When solving quadratic equations by completing the square, first rewrite the function in standard form, ax² + bx + c = 0. If the value of a is greater than zero (a>0), then divide the whole equation by a such that the coefficient of x² is equal to one. The quadratic equation is now of the form x² + b/ax + c/a = 0.
Next, put the constant c/a on the right-hand side of the equation to get x² + b/ax = -c/a. To complete the square, write the left-hand side of the equation (x² + b/ax) as a perfect square trinomial by adding (b/2a)² to both sides of the equation, so that you have the expression x² + b/ax + (b/2a)² = -c/a+(b/2a)². To continue this process, factor and evaluate the equation.
Extract the square of the squared binomial by taking the square root of both sides of the equation; the result is a linear equation. Finally, solve the equation by simply isolating the variable x.
Notice that some quadratic equations have two solutions, some have one solution, and some even have two imaginary solutions.
Solve quadratic equations in one variable.
CCSS.MATH.CONTENT.HSA.REI.B.4.A
Transcript Finding the Value that Completes the Square
General Good is staking out a warehouse where a high-priority target is located. General Good's mission, should she choose to accept, is to find the values that complete the square.
Let's take a closer look at the General's mission objectives. She must rescue the hostage, Prince Fluffington IV and return him safely to his family. To rescue the prince, General Good must stay in the shadows as she jumps from the roof of one building to another with the aid of her trusty jetpack. The flight path of the jetpack is in the shape of a parabola and can be written as a quadratic function, so before she can rescue the hostage, General Good needs to make some calculations.
f(x) and h(x)
The jetpack has two different settings, f(x) and h(x). So to rescue the prince, she has to select the correct one so she can land her jump right inside the airshaft. Let’s draw a coordinate system. We can plot her path on the x- and y-axis. Lucky for us, we know the equation of the two possible flight paths.
Let's take a look at the first one. Since she needs to solve for the roots she sets the quadratic function equal to zero. Okay! Now to complete the square. General Good modifies the equation so the coefficient of the highest power is equal to one. Next, move the constant to the right side of the equal sign and then find the c-value that changes the left side of the equation to have the format of a perfect square trinomial: a² + 2ab+b².
To do this, divide the coefficient of the x-term by 2 and then square it, so -80 divided by 2 and squared is equal to 1600. This is the value that *completes the square. Remember, whatever we add or subtract on one side of the equation, we also must do to the other. Watch and learn!
Factoring and solving for x
Now we can factor the trinomial. Then take the square root of each side and solve for x. As you can see, if General Good chooses this flight path, it'll land her short of the airshaft. So, let’s take a look at the second option. If it doesn't work, I don't know what General Good'll do. Again, we have to complete the square. Set the equation equal to zero. Modify the equation so that the coefficient of the highest power is equal to 1.
Use opposite operations to write the constant on the right side of the equal sign. Find a c-value that creates a perfect square trinomial by dividing the coefficient of the x-value in half and squaring it. Add the c-value to both sides of the equation. Now, factor the trinomial. Take the square root of each side and solve. x is equal to 10 and 90. Thank goodness! The second flight path will work! Whew, I thought jumping between the buildings would be the difficult part of this story.
As expected, General Good lands her jump and rescues the prince, but he’s not exactly what she expected.
Finding the Value that Completes the Square exercise
-
Explain how to solve the given function.
HintsThe standard form of a quadratic equation is given by $ax^2+bx+c=0$.
Keep the following in mind:
$(a+b)^2=a^2+2ab-b^2$ or $(a-b)^2=a^2-2ab-b^2$.
$x^2+bx+c=0$ is equivalent to $x^2+bx+\left(\frac b2\right)^2=-c+\left(\frac b2\right)^2$.
Factoring, we get $x^2+bx+\left(\frac b2\right)^2=\left(x+\frac b2\right)^2$.
SolutionHow should one solve such an equation?
- First rewrite the equation so that the coefficient of the highest power is equal to $1$: we have to multiply by $-45$. This leads to $x^2-80x+700=0$.
- Next move the constant to the right using opposite operations: $x^2-80x=-700$.
- Now find the $c$ value to form a perfect square trinomial, namely $c=\left(\frac{-80}2\right)^2=40^2=1600$.
- Add this value on both sides of the equation and combine the terms on the right-hand side: $x^2-80x+1600=-700+1600=900$.
- Factor the trinomial on the left-hand side: $(x-40)^2=900$.
- Almost done: take the square root on both sides to get $x-40=\pm 30$.
- Last but not least you get the solutions by adding $40$ on both sides: $x=30+40=70$ or $x=-30+40=10$.
-
Solve the given quadratic equation.
HintsLet's have a look at $x^2+4x-5=0$:
- Add $5$ to $x^2+4x=5$.
- $c=\left(\frac42\right)^2=4$
- Add $c=4$ to $x^2+4x+4=9$.
Looking at $(a+b)^2=a^2+2ab+b^2$ and the trinomial $x^2+4x+4$, we can conclude that $a=x$ and $b=2$. We then have that
$(x+2)^2=x^2+2x(2)+2^2=x^2+4x+4$.
Now we can proceed as follows: $x^2+4x+4=9$ is equivalent to
$(x+2)^2=9$.
Now we take the square root to get $x+2=\pm 3$.
Last we subtract $2$ to get the solutions
$x=3-2=1$
or
$x=-3-2=-5$.
SolutionLet's practice finding the solution of a quadratic equation by finding the value that completes the square:
- Divide the equation on both sides by $-0.01$ to get the coefficient of the highest power equal to $1$: $x^2-100x+900=0$.
- Move the constant to the right: $x^2-100x=-900$.
- Now we have to do the main part of the work: find the $c$ value to form a perfect square trinomial, namely $c=\left(\frac{-100}2\right)^2=50^2=2500$.
- Add this value to both sides of the equation: $x^2-100x+2500=-900+2500=1600$.
- Factor the trinomial: $(x-50)^2=1600$.
- Take the square root: $x-50=\pm 40$.
- Add $50$ to get the solutions $x=40+50=90$ or $x=-40+50=10$.
-
Find the missing value $c$ that completes the square.
HintsTake a look at a quadratic binomial
$x^2+2bx$.
The missing value completes this term to
$x^2+2bx+b^2-b^2=(x+b)^2-b^2$.
In general the missing term is given as the square of the coefficient of the linear term divided by $2$.
Let's have a look at another example, $x^2+6x$.
The missing term is $\left(\frac62\right)^2=3^2=9$.
SolutionFor $x^2+bx$, the missing value $c$ is given by $c=\left(\frac b2\right)^2$.
Adding this value to the binomial above we get a perfect square trinomial which we can factor out.
- $x^2+12x$ - here we have $b=12$. Squaring half of it gives us $c=\left(\frac{12}2\right)^2=6^2=36$.
- $x^2-8x$ - we can conclude with $b=12$ that $c=\left(\frac{-8}2\right)^2=4^2=16$.
- $x^2+16x$ - with $b=12$ we get $c=\left(\frac{16}2\right)^2=8^2=64$.
- $x^2+18x$ - here we have $b=18$. Thus we get $c=\left(\frac{18}2\right)^2=9^2=81$.
-
Decide which equation(s) will give General Good's jetpack the right distance to jump.
HintsAll the trinomials on the left-hand sides are given in perfect square form.
For example, we have $x^2+140x+4900=(x+70)^2$.
After factoring, take the square of both sides.
Let's have a look at an example:
$(x+4)^2=16$.
This leads to $x+4=\pm 4$.
Subtracting $4$ on both sides leads to $x=-8$ or $x=0$.
Here we have the distance $|-8-0|=8$.
SolutionWe solve each equation above and subtract the resulting solutions to check if the distance is $80$.
Each trinomial is in a perfect square form:
- $x^2-120x+3600=1600$ is equivalent to $(x-60)^2=1600$. Taking the square root gives us $x-60=\pm 40$ and thus $x=40+60=100$ or $x=-40+60=20$. The difference of both solutions is $100-20=80$ $~~~~$✓
- $x^2-120x+3600=900$ is equivalent to $(x-60)^2=1600$. Again taking the square root leads to $x-60=\pm 30$ and thus $x=30+60=90$ or $x=-30+60=30$. The difference of both solutions is $90-30=60$. This equation would not help her get from tree to tree.
- $x^2+80x+1600=2500$ - we rewrite this as $(x+40)^2=2500$ and take the square root to $x+40=\pm 50$. The resulting solutions are $x=50-40=10$ or $x=-50-40=-90$. The difference of both solutions is $10-(-90)=100$. This equation would not help her get from tree to tree.
- $x^2+80x+1600=1600$ - the difference to the equation above is the right side: $(x+40)^2=1600$. Taking the square root results in $x+40=\pm 40$ and the solutions are $x=40-40=0$ or $x=-40-40=-80$. The difference of both solutions is $0-(-80)=80$ $~~~~$✓
- $x^2+140x+4900=1600$ - factoring leads to $(x+70)^2=1600$. Now we take the square root to $x+70=\pm 40$ to get the solutions $x=40-70=-30$ or $x=-40-70=-110$. The difference of those solutions is $-30-(-110)=80$ $~~~~$✓
- $x^2-140x+4900=2500$ leads to $(x-70)^2=4900$ and, by taking the square root, to $x-70=\pm70$. This gives us the solutions $x=70-70=0$ or $x=-70-70=-140$ with the difference $0-(-140)=140$. This equation would not help her get from tree to tree.
-
Identify the polynomial which is equal to $(a+b)^2$.
HintsFactor out the squared binomial $(a+b)^2=(a+b)(a+b)$ using the FOIL method.
For example, $x^2+6x+9=(x+3)^2$.
SolutionFinding the value that completes the square leads to the following:
$(a+b)^2=a^2+2ab+b^2$.
So if you already have a binomial like $x^2+6x$ you have to find a value that completes this binomial to a perfect trinomial which can be factored.
This value for $x^2+6x$ is $\left(\frac62\right)^2=3^2=9$, giving us that
$x^2+6x+9-9=(x+3)^2-9$.
The trinomial on the left $x^2+6x+9$ is the desired perfect trinomial.
-
Find the two solutions of the following equation.
HintsYou have to divide both sides of the equation by the coefficient of the highest power, unless it is already $1$.
The value $c$ completing the square of $x^2+bx$ is given by $c=\left(\frac b2\right)^2$.
You can check your solutions by putting them in the equation above.
SolutionStep by step we solve the equation:
- Divide by $4$ to get a coefficient of the highest power equal to $1$: $x^2+8x-20=0$.
- Move the constant to the right: $x^2+8x=20$.
- The value that completes the square on the left to a perfect square trinomial is given by $c=\left(\frac82\right)^2=4^2=16$.
- Add $c=16$: $x^2+8x+16=20+16=36$.
- Factor the trinomial: $(x+4)^2=36$.
- Take the square root: $x+4=\pm 6$.
- Last but not least, you get the solutions by subtracting $4$ on both sides: $x=6-4=2$ or $x=-6-4=-10$.
What are Quadratic Functions?
Graphing Quadratic Functions
FOILing and Explanation for FOIL

Solving Quadratic Equations by Taking Square Roots
Solving Quadratic Equations by Factoring
Factoring with Grouping

Solving Quadratic Equations Using the Quadratic Formula

Solving Quadratic Equations by Completing the Square
Finding the Value that Completes the Square
Using and Understanding the Discriminant
Word Problems with Quadratic Equations











