Factoring with Grouping
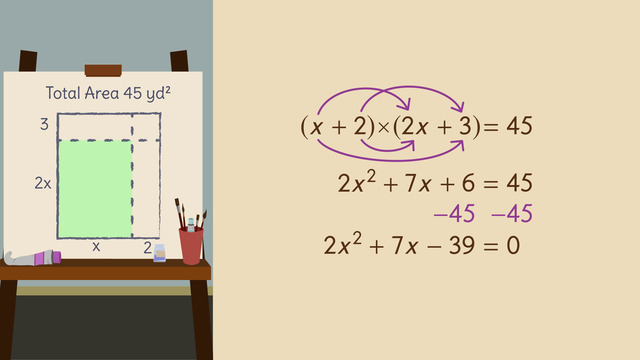

Basics on the topic Factoring with Grouping
There are easy ways to solve this quadratic equations, like 3x2 - 25x + 56 = 14. One way is by combining factoring and grouping.
The standard form of the quadratic equation is given by ax2 + bx + c = 0.
Once such an equation is put into standard form, we can then determine its factors by finding the factors of a*c such that a+c=b.
For example, the equation 3x2 - 25x + 56 = 14 in standard form is 3x2 - 25x + 42 = 0, with a = 3, b = -25, and c = 42.
We can then see that (a * c) = 3 * 42 = 126, which has the factors:
Factors | 1,126 | -1,-126 | 2,63 | -2,-63 | 3,42 | -3,-42 | 6,21 | -6,-21 | 7,18 | -7,-18 | Sum | 127 | -127 | 65 | -65 | 45 | -45 | 27 | -27 | 25 | -25 |
with (-7,-18) fulfilling the statement a + c = b: (-7) + (-18) = -25.
Rewriting our equation as 3x2 - 7x - 18x + 42 = 0, and grouping it as (3x2 - 7x) - (18x - 42) = 0, we can factor x from the first group and 6 from the second group to get x (x - 7) - 6 (x - 7) = 0. We can then isolate (x - 7) as a common factor and finally get the equation: (x - 6)(x - 7) = 0.
We have thus factored 3x2 - 25x + 42 = 0 into (x - 6)(x - 7) = 0, from which we can finally see that either x = 6 or x = 7.
Analyze Functions Using Different Representations.
CCSS.MATH.CONTENT.HSF.IF.C.8.A
Transcript Factoring with Grouping
Meet Vincent. He’s a painter and quite the eccentric. He just got a new commission, to embellish the façade of an old building on the fancy side of the town. The neighbors just want the ugly wall to disappear. For inspiration, he goes to take a look at the building. Those darn kids – they painted graffiti all over it. No matter, Vincent will paint over the mess. To help him cover the graffiti, Vincent can solve quadratic equations by factoring and grouping.
Back at home, as he considers the specifics of the building, he divises a strategy. What does he know? The front of the building is equal to an area of 45 yards squared, but not to be included in the painting is the fire escape on the right side of the building, it's 2 yards wide, and the windows at the top of the building, they have a height of 3 yards. The painting must be in the shape of a rectangle with the height equal to 2 times the width. Because he doesn’t know the width or the height, he uses the variables, x and 2x.
Setting up an equation
He sets up an equation and sets the total area equal to 45 yards squared. The quantity x plus 2 times the quantity 2x plus 3 is equal to 45. To calculate x, first we FOIL. Then, we combine like terms. Next, since this is a quadratic equation, to find the solution, we modify the equation - so it's equal to 0.
Factoring by Grouping
Now we're ready to factor with grouping. First, find the factors of ac that sum to b. ac is equal to 2 times -39, so -78. b is 7. Now what factors of -78 sum to 7? Hmmm, let’s go through the list. Ahah, -6 and 13 will work. Now, we split up 7x into two terms, -6x and 13x. Pay close attention to this next step: use parentheses to group the 4 terms into 2 binomials and then factor out the GCF from each binomial. This can be tricky, so watch carefully. The end result is the binomial: x - 3 times the binomial 2x + 13, and the product is equal to zero. But not so fast, we have one last step.
Apply the Zero Product Property and solve for both values of 'x'. There one last thing to think about with this problem. You can’t have a negative length or width, so only one of the solutions is a possible answer. X is equal to 3 yards, so the height of the painting is equal to 6 yards and the width is equal to 3 yards.
Now that the math is done, Vincent can work on his masterpiece…
Factoring with Grouping exercise
-
Establish the equation corresponding to the area of the façade of the building.
HintsThe area of a rectangle is given by its height multiplied by its width.
Look at this rectangle representing the house wall:
SolutionThis rectangle represents the house wall.
We calculate the area by multiplying the height by the width of the rectangle:
- The height is given by $2x+3$.
- The width is given by $x+2$.
$(2x+3)\times (x+2)$
Given that the area of the rectangle is $45$ yards squared, we have that
$(2x+3)\times(x+2)=45$
-
Solve the equation describing the area of the building to be painted.
HintsFOIL multiplication means:
- Multiply the First.
- Multiply the Outer.
- Multiply the Inner.
- Multiply the Last.
If you multiply any term by zero the product is also zero.
SolutionFirst, we use the FOIL method to factor the left-hand side of the equation:
- Multiply the First to get $2x^2$.
- Multiply the Outer to get $3x$.
- Multiply the Inner to get $4x$.
- Multiply the Last to get $6$.
Combining like terms gives us $2x^2+7x+6=45$.
Then subtract $45$ from both sides of the equation to get $2x^2+7x-39=0$.
Now we are looking for the factors of $2\times (-39)=-78$ which sum to $7$:
- $-1\times 78=-78$ but $-1+78=-77$
- ...
- $6\times (-13)=-78$ but $6+(-13)=-7$
- $-6\times 13=-78$ and $-6+13=7$ $~~~~$✓
$(2x^2-6x)+(13x-39)=0$
and factor both terms inside the parenthesis:
$2x(x-3)+13(x-3)=0$
Again factoring, we get $(2x+13)\times (x-3)=0$. The zero product property tells us that we get either $2x+13=0$ or $x-3=0$.
$\begin{array}{rcr} 2x+13 & = & 0\\ \color{#669900}{-13} & &\color{#669900}{-13}\\ 2x & = & -13\\ \color{#669900}{\div2} & & \color{#669900}{\div2}\\ x & = & -6.5 \end{array}$
This can't be a solution in our case because $x$ is a length and thus cannot be negative.
$\begin{array}{rcr} x-3 & = & 0\\ \color{#669900}{+3} & &\color{#669900}{+3}\\ x & = & 3\\ \end{array}$
This is the solution we want. So the part of the building to paint is 6 yds. high and 3 yds. wide.
-
Find the mistakes in Vincent's calculations.
HintsHere you see an example for the FOIL multiplication:
$(x+4)\times (x+5)=...$
- Multiply the First to get $x\times x=x^2$.
- Multiply the Outer to get $x\times 5=5x$.
- Multiply the Inner to get $4\times x=4x$.
- Multiply the Last to get $4\times 5=20$.
$...x^2+9x+20$
Keep in mind that you only can combine like terms; for example, $2x+3x=5x$, but you can't combine anymore terms in $2x+3x^2$.
SolutionThe FOIL method for multiplying binomials:
- First
- Outer
- Inner
- Last
Supermarket
$\begin{array}{rclll} (3x+1)\times(2x+2)&=&3x\times 2x+3x\times 2+1\times 2x+1\times 2\\ &=&6x^2+6x+2x+2&|&\text{ combining like terms}\\ &=&6x^2+8x+2 \end{array}$
School
$\begin{array}{rclll} (4x+1)\times(x+5)&=&4x\times x+4x\times 5+1\times x+1\times 5\\ &=&4x^2+20x+x+5&|&\text{ combining like terms}\\ &=&4x^2+21x+5 \end{array}$
City hall
$\begin{array}{rclll} (x+2)\times(5x+1)&=&x\times 5x+x\times 1+2\times 5x+2\times 1\\ &=&5x^2+x+10x+2&|&\text{ combining like terms}\\ &=&5x^2+11x+2 \end{array}$
-
Factor each trinomial.
HintsYou can check the factorization using the FOIL method.
If you multiply the factors of the linear terms of each binomial you get the factor of the resulting quadratic term of the trinomial.
SolutionIf you want to get a factor a trinomial,
$ax^2+bx+c=0$,
you have to find the factors of $a\times c$ which sum to $b$.
The other way is to check if a given factorization is correct using the FOIL method.
Let's start with $3x^2+4x-4=0$. We need to find all factors of $3\times (-4)=-12$ and choose the pair which sums to $4$.
- $-1\times 12=-12$ but $-1+12=-11$
- ...
- $2\times(-6)=-12$ but $2+(-6)=-4$
- $-2\times 6=-12$ and $-2+6=4$.
$3x^2+4x-4=(3x^2+6x)-(2x+4)=3x(x+2)-2(x+2)=(3x-2)\times(x+2)$.
Let's try just another example: $-6x^2+2x+4=0$. Find all factors of $-6\times 4=-24$ and choose the pair which sum to $2$. We have that $-4\times 6=-24$ and $-4+6=2$, so we have:
$-6x^2+2x+4=-6x^2-4x+6x+4=-2x(3x+2)+2(3x+2)=(-2x+2)\times(3x+2)$.
The other way is to use the FOIL method:
$(4x+4)\times(2x-3)=4x\times 2x+4x\times (-3)+4\times 2x+4\times (-3)$.
Combining like terms we get $...=8x^2-12x+8x-12=8x^2-4x-12$.
Last but not least we look at $(-x+3)\times(3x-1)=-x\times 3x-x\times (-1)+3\times 3x+3\times (-1)$. We can simplify this by combining like terms:
$...=-3x^2+x+9x-3=-3x^2+10x-3$.
-
Determine the solutions and decide which solution is a reasonable length.
HintsEach factor gives a solution.
Check each solution, keeping in mind that $x$ represents a length.
SolutionWe start with the equation
$(2x+13)\times (x-3)=0$.
By the zero product property, we get that either $2x+13=0$ or $x-3=0$.
$\begin{array}{rcr} 2x+13 & = & ~0\\ \color{#669900}{-13} & &\color{#669900}{-13}\\ 2x & = & ~-13\\ \color{#669900}{\div2} & & \color{#669900}{\div2}\\ x & = & ~-6.5 \end{array}$
This can't be a solution, because $x$ is a length and thus cannot be negative.
$\begin{array}{rcr} x-3 & = & ~0\\ \color{#669900}{+3} & &\color{#669900}{+3}\\ x & = & ~3\\ \end{array}$
This is the desired solution. The part of the house wall to paint is 6 yds. high and 3 yds. wide.
-
Determine the solutions of the equation.
HintsUse FOIL multiplication to factor:
- Multiply the First.
- Multiply the Outer.
- Multiply the Inner.
- Multiply the Last.
You have to find the factors of $-114$ which sum to $13$.
Check your solutions (one is a decimal number) by inserting them into the equation above.
SolutionFirst, we use FOIL multiplication to factor:
- Multiply the First to get $2x\times x=2x^2$.
- Multiply the Outer to get $2x\times 4=8x$.
- Multiply the Inner to $5x$.
- Multiply the Last to get $5\times 4=20$.
Subtracting $77$ on both sides gives us $2x^2+13x-57=0$.
Now we are looking for the factors of $2\times (-57)=-114$ which sum to $13$:
$-6\times 19=-114$ and $-6+19=13$. $~~~~$✓
Now we can proceed by rewriting the equation above as
$(2x^2-6x)+(19x-57)=2x(x-3)+19(x-3)=(2x+19)\times (x-3)=0$.
Because a product equals zero if one of the factors equals zero we get either $2x+19=0$ or $x-3=0$.
$~$
$\begin{array}{rcr} 2x+19 & = & ~0\\ \color{#669900}{-19} & &\color{#669900}{-19}\\ 2x & = & ~-19\\ \color{#669900}{\div2} & & \color{#669900}{\div2}\\ x & = & ~-9.5 \end{array}$or
$\begin{array}{rcr} x-3 & = & ~0\\ \color{#669900}{+3} & &\color{#669900}{+3}\\ x & = & ~3\\ \end{array}$
$~$
Those are the wanted solutions: Either $x=-9.5$ or $x=3$.
What are Quadratic Functions?
Graphing Quadratic Functions
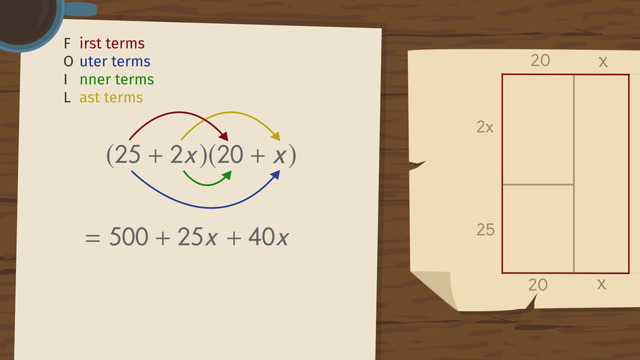
FOILing and Explanation for FOIL

Solving Quadratic Equations by Taking Square Roots
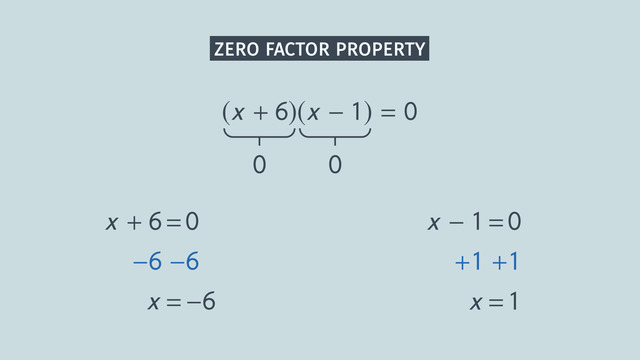
Solving Quadratic Equations by Factoring
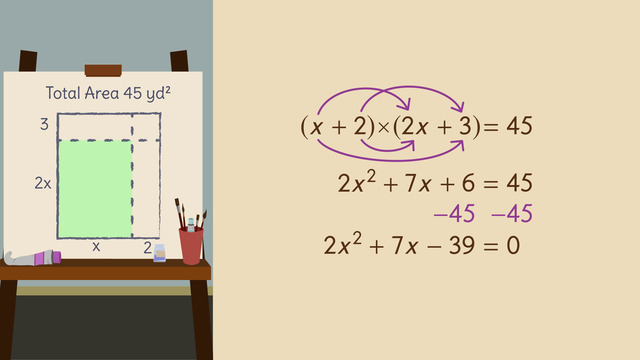
Factoring with Grouping

Solving Quadratic Equations Using the Quadratic Formula

Solving Quadratic Equations by Completing the Square
Finding the Value that Completes the Square
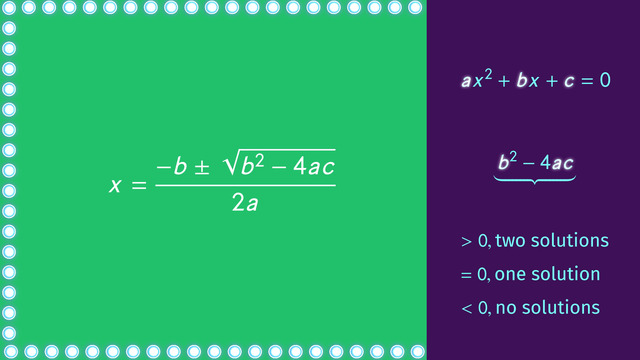
Using and Understanding the Discriminant
Word Problems with Quadratic Equations











