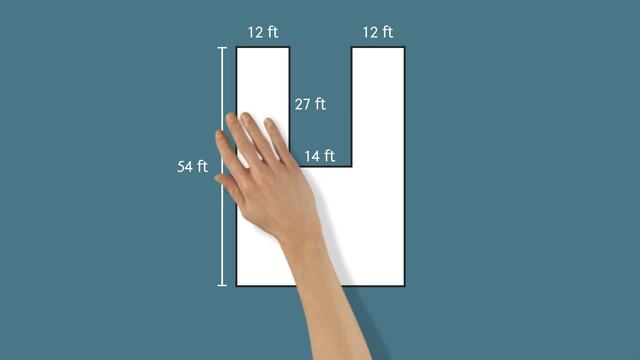
Composite Area Problems

Basics on the topic Composite Area Problems
After this lesson, you will be able to find the areas of partial regions of composite shapes.
The lesson begins by teaching you that composite figures can be decomposed into smaller shapes. It leads you to learn how partial areas can be found by adding or subtracting the areas of these shapes. It concludes with a few strategies for determining missing values in composite area problems.
Learn about composite area problems by helping Timmy get the temporary tattoo of his dreams!
This video includes key concepts, notation, and vocabulary such as composite figures (shapes composed of smaller shapes), and partial areas (areas often represented as the shaded region in a composite shape).
Before watching this video, you should already be familiar with the formulas for the areas of various regions, including quadrilaterals, triangles, circles, and semicircles. You should also know how to use composition and decomposition to find the areas of shapes.
After watching this video, you will be prepared to learn how to determine the areas of complex partial and composite shapes.
Common Core Standard(s) in focus: 7.G.B.4, 7.G.B.6 A video intended for math students in the 8th grade Recommended for students who are 13 - 14 years old
Transcript Composite Area Problems
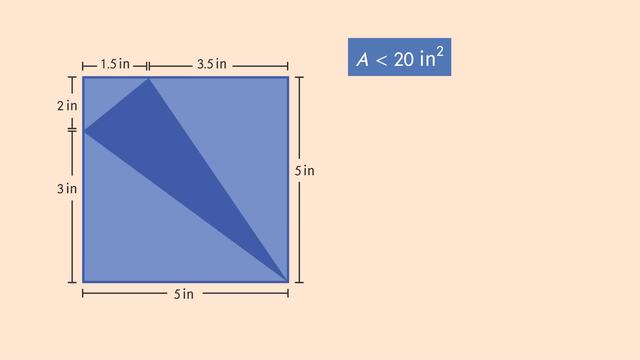
It's the annual school summer fest and everybody wants to get in on the action at the temporary tattoo stand. But Timmy has been holding up the line all day! He just needs a couple shapes to complete his design, but he's working on a limited budget. To figure out if he can complete his masterpiece we'll need to solve Timmy's composite area problems. Timmy has enough money for two small designs, which each have to have an area of less than 20 square inches. The first shape he wants done is this shaded triangle, which we can call, 'd'. We know that triangle 'd' is part of a larger composite shape. This composite is a square composed of our triangle 'd' plus three additional triangles, which we can call 'a,' 'b' and 'c' Now, can you think of a way we could calculate the area of triangle 'd' using the areas of these other shapes? If we find the area of the square...and subtract the areas of triangles 'a,' 'b'and 'c' we will be left with the area of triangle 'd'. Let's start with the area of the composite square. We know the dimensions of the square are 5 inches by 5 inches so the area of the entire composite is 25 square inches. Now before we move on, we need the formula for the area of a triangle. Area equals one-half base times height. Remember, because 'a', 'b', and 'c', are all right triangles, their perpendicular side lengths are also their respective bases and heights. So let's calculate their areas, starting with triangle 'a'. This triangle has a base of 5 and height of 3 giving it an area of 7.5 square inches. To find the area of triangle 'b' we use side lengths 3.5 and 5 giving us an area of 8.75 square inches. The area of triangle 'c' can be found by multiplying one-half times 1.5 times 2 which gives us 1.5 square inches. Substituting these values into our equation and subtracting we see that triangle 'd' has an area of 7.25 square inches. That is well under his limit of 20 square inches for a small design. So Timmy gives the temporary tattoo artist the signal and braces himself! No pain, no gain! There's just one more missing shape in Timmy's design. This temporary tattoo includes just the shaded region in the diagram. Let's see if this partial area fits in our price range for a small design of less than 20 square inches. In order to calculate the area, we'll need to identify the different shapes that make up this composite. What shapes do you see? Well there are definitely circles here but what if we use partial circles? Notice that the upper portion of the design is a semicircle, which we can call 'a'. We'll need to include that area in our calculation, so let's add that to our equation. We'll also need to calculate the area of this semicircle, 'b'. But we don't want to include the area of this smaller semicircle, 'c' so we'll SUBTRACT that area. Ok, now that we have a plan, let's calculate the areas of the semicircles! Remember, a semicircle is half of a circle, so we can use the formula, area equals ONE-HALF pi 'r' squared. Turning our attention to semicircle 'a' we have a radius of 2 inches which gives us an area of 2 pi square inches. Semicircle 'b' has a radius of 3 inches which gives us an area of 4.5 pi square inches. Semicircle 'c' has a radius of 1 inch and an area of 0.5 pi square inches. Substituting these values into our equation and calculating we find the area of the design is exactly 6 pi square inches. If we approximate pi using 3.14, that gives us about 18.84 square inches. That puts us just under our limit for the area of a small design. So, while Timmy gets tatted up let's review. Composite shapes are figures that are composed of smaller shapes, like triangles, squares, and semicircles. To find a partial area in a composite, start by identifying the shapes which compose it. Then, use those areas to write an equation which expresses the area you want to find, in terms of the other areas in the composite. Partial areas that you want to include in your calculation should be represented with addition. For partial areas that you do NOT want to include in your final calculaiton, just use subtraction to represent taking these areas away. Coming in just under his budget, Timmy's temporary masterpiece is complete. No... re-gets? Oof, that tattoo artist really needs a spellchecker.