Finding the Area of Polygons Using Decomposition

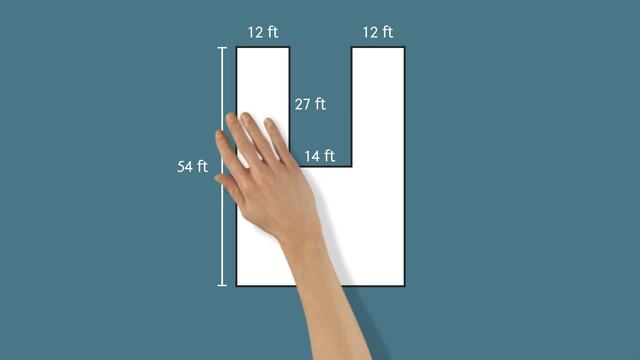
This is Prince Icarus, an ostrich with a problem. As Prince, he can have whatever his heart desires, except for one thing. He'll never be able to fly. Today, the Prince is receiving a special visitor who wants to give him a taste of what it's like to defy gravity. All he has to do, is turn his throne room into a giant trampoline park! But in order to do that, we will need to find the area of polygons using decomposition. This blueprint shows the layout of the throne room floor. The kangaroo proposes to cover the whole area of this shape with trampolines. The polygon in the blueprint is a composite, which just means it's made up of other shapes, like rectangles. We can find the area of composite polygons with decomposition, which means breaking apart into smaller shapes. How would you break apart this polygon into three smaller, rectangular shapes? One way to decompose the throne room floor, would be to create three rectangles, which we can call 'A', 'B' and 'C'. If we add the areas of 'A', 'B' and 'C', that will give us the total area of the polygon. Let's start with finding the area of 'A'. This rectangle has side lengths of 27 feet and 12 feet. So, how do we find the area? Multiplying the side lengths together we determine the area of rectangle 'A' is 324 square feet. We can substitute this value into our formula for 'A'. Now let's look at rectangle 'B'. Notice anything familiar about this shape? Although one side of rectangle 'B' is not labeled with a length, we can see that it is in fact the same size as 'A'. So we know that rectangle 'B' also has an area of 324 square feet. But, what about rectangle C? Neither side length of this rectangle is labeled, but do you see any clues that could help us figure out the missing measurements? We know the bottom side has the same length of these three sides combined so we can find the total length by adding 12 feet plus 14 feet plus 12 feet. That gives us a total of 38 feet for the bottom side. Now how can we use what we know to find the length of the vertical sides of rectangle 'C'? Well we can see that the entire left side of the polygon is 54 feet. We can also see that rectangle 'A' has one side length of 27 feet. That means the missing side length of rectangle 'C' is equal to 54 feet minus 27 feet which is 27 feet. Multiplying our side lengths together we get an area of 1,026 square feet, for Rectangle 'C'. Adding all three rectangular regions together we have an area of 1,674 square feet for the composite polygon! To check our work, let's try a different method, by decomposing the polygon into just two rectangles. Can you see two rectangles in this shape? If we draw a line connecting the top, we can see there is a large rectangle, outlining the entire polygon, which we will call 'D' and a cut-out rectangle inside it, which we will call 'E'. How can we use these two shapes to determine the area of the whole composite? If we find the area of the large rectangle 'D' and subtract the cut-out rectangle 'E' that will leave us with the total area of the polygon. The area of the large rectangle, 'D', is 38 times 54 which is 2,052 square feet. The area of the smaller rectangle is 14 times 27 which is 378 square feet. Substituting these areas into our formula confirms that the total area of the throne room is 1,674 square feet. While Prince Icarus is trying out his new trampoline park let's review how to find the area of polygons using decomposition. The first step is to decompose your polygon into smaller shapes. Then, make a plan for finding the total area of the polygon, using addition to combine areas and subtraction to take them away. Next, find any missing lengths you need, using the information you have. Then, calculate the areas of each shape and substitute them into your problem solving plan! It looks like Prince Icarus's dreams of flight have finally come true! Yeah, maybe this is going to take some getting used to.