Using Substitution to Solve Systems of Linear Equations


Basics on the topic Using Substitution to Solve Systems of Linear Equations
After this lesson, you will be able to use the substitution method to write the solution for a system of linear equations.
The lesson begins with a review of how to use the graph of two lines to find a solution to a system of linear equations. It then outlines a strategy for using algebraic substitution to solve systems of linear equations, without graphing.
Learn how to solve system of linear equations with substitution by helping Valdemar get his ax back!
This video includes key concepts, notation, and vocabulary such as: system of equations (a set of equations which occurs simultaneously), linear equation (an equation between two variables that gives a straight line when graphed), and substitution method (a method used to solve a system of linear equations).
Before watching this video, you should already be familiar with estimating the solution to a system of equations by finding the point of intersection on a graph.
After watching this video, you will be prepared to learn more about using algebra to solve systems of equations.
Common Core Standard(s) in focus: 8.EE.B.5, 8.EE.C.8 A video intended for math students in the 8th grade Recommended for students who are 13 - 14 years old
Transcript Using Substitution to Solve Systems of Linear Equations
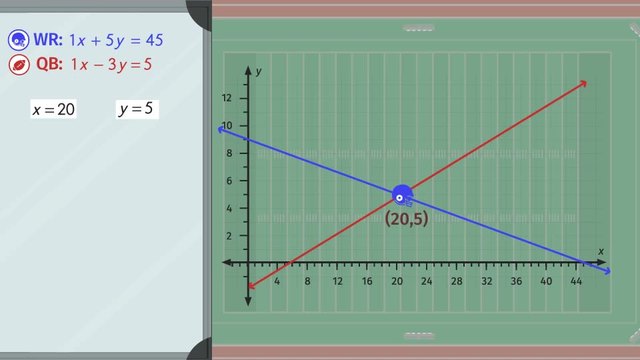
Ah, another peaceful morning in Foglandia. Hey, Valdemar! Wake up! Your prized battle axe is missing! It must be that no-good thief, Evil Erik! And he’s already making a getaway! Valdemar gathers his best men and his fastest ship to chase Evil Erik down. But will he catch him in time? Let’s help Valdemar get his battle axe back by Solving Systems of Linear Equations with the Substitution Method. Here we have a line that describes Evil Erik's progress across the ocean at 'y' equals 15x plus 40 . But what's that? Valdemar's ship is quickly catching up with Evil Erik and can be represented by the equation 'y' equals 20x. Know that the point of intersection is the solution to the system of equations and tells us when and where Valdemar finally catches up to Evil Erik! But this point is kind of difficult to make out. And while graphing is a very nice way to visualize the problem and solution, don't you find it sometimes pretty time consuming? We don't always have to graph lines to find the point of intersection. We can just use the algebraic substitution method. Remember substitution is the action of replacing something with another thing. Therefore, in mathematics the substitution method of solving a system of equations is used when one of the equations is solved for one variable in terms of the other variable. Additionally, a solution to a linear system must satisfy all of the equations. That means we have to find an 'x' and a 'y' value that work in BOTH equations. Luckily, the equations we have are perfect for substitution since at least one of them already has an isolated variable. Looking at the second equation, we see that 'y' equals 20x. So, using the first equation we can just substitute the 20x in for the 'y.'
This gives us 20x equals 15x plus 40. Now we only have one unknown and we've solved these types of equations before, right? Remember to first move all terms with variables to one side. To do this we subtract the 15x from the right and left sides of the equation to keep it balanced. This gives us 5x equals 40. Next, we isolate the 'x' variable. How do we do this? By dividing both sides by 5 giving us 'x' equals 8. So far so good, but don't stop here. We still need to find 'y'. Using the second ORIGINAL equation we can substitute the 8 for 'x' to get 'y.' Multiplying 20 by 8 gives us 'y' equals 160. So, the solution to this system of equations is 'x' equals 8 and 'y' equals 160. Nevertheless, something super nice about this algebra is that we can always CHECK OUR ANSWERS. Let's use our original first equation and plug in the values for 'x' and 'y' to double check. Since we're checking we ask does 160 equal 15 times 8, plus 40? 160 does equal 160. Great! Our solution is right! So we can write this solution as the point (8, 160). Which looks like the correct point on the graph too! Awesome!!! Now let's take a look at another system of linear equations. Again, our goal is to find the solution. That is an 'x' and a 'y' value that work for both equations. When using substitution it's nice to have already isolated variables. However, we don't have any isolated variables here. So what do we do? We could pick any variable from either equation to isolate. It's really up to you. A good choice is the variable that's easiest to isolate. Since the 'x' in the first equation has a coefficient of 1, it's the easiest to isolate. We can do this by adding 5y to both sides. This gives us 'x' equals negative 3 plus 5y. We can substitute this expression in for 'x' in the second equation. Notice that we only have y-variables now. So, first simplify both sides. Remember, we can use the distributive property to get rid of the parentheses then combine like terms. Now isolate 'y', by subtracting 24 from both sides and dividing both sides by negative 37. We see that 'y' equals zero. But keep going! We still need to solve for 'x'. To do this, go back to our ORIGINAL first equation and substitute zero for 'y' and solve for 'x.' Giving us 'x' equals negative 3. Now let's use the second equation to check if the solution 'x' equals negative 3 and 'y' equals zero works for both equations. Nice, both sides simplify to the same number. Therefore, we can confidently write our solution as the point (-3, 0). Problem solved and no graphing required! To review solving a system of linear equations using the substitution method, follow these steps: Begin by isolating any variable. Then, using this expression substitute and solve for the first variable. Next, substitute and solve for the second variable. Remember! You can check your work by substituting the point into the unused equation! Finally, write the solution as an ordered pair. Let's see how Valdemar's quest to retrieve his stolen axe is progressing! It looks like Evil Erik's about to get what's coming to him or maybe that battle axe was just for show.
Using Substitution to Solve Systems of Linear Equations exercise
-
Recall the steps for solving a system of two linear equations.
HintsTo substitute means to replace something for something else . In order to substitute, at least one of the equations should have an isolated variable.
To solve a system you need to solve for both $x$ and $y$. Use the isolated variable to determine which variable you will solve for first.
Once you have found one variable, substitute it back into one of the equations to solve for the remaining variable.
A solution to a system must make both equations true. Check to make sure the $x$ and $y$ values you found work in both equations.
A solution to a system of equations is the point where the graphs of the equations meet, or the values that make both equations true.
SolutionThe steps to solve a system of equations by substitution are:
- Isolate any variable.
- Before you can start to solve a system of equations by substitution, you need to have at least one equation with a variable isolated so that you can substitute it into the other equation.
- To solve an equation for a variable, you need to only have one variable in the equation. Substituting helps by changing one of the variables in terms of the other variable, this way you can solve the equation for either $x$ or $y$ and get a numerical answer.
- Now that you know the value of one of the variables you can substitute that value into either one of the equations. Remember the goal when solving a system of equations is to find the point, $(x,y)$, that makes both equations true. You must continue the process until you've found both variables.
- After substituting for one of the variables, you now can solve for the remaining variable. Now you have both the $x$ and $y$ values for the solution.
- To make sure that you did not make a mistake in calculations, it is important to check to make sure that the $x$ and $y$ values work in both of the equations. Substitute both values into each equation and simplify. The values work in the equation if the left and right side of the equations are equal to each other (for example, $12=12$). Once you have determined the values work in both equations, write your answer as an ordered pair, $(x,y)$.
-
Identify the solution to the system of linear equations using the substitution method.
HintsTo use the substitution method, at least one of the equations must have a variable that is isolated. To isolate a variable, use the opposite operation to move terms and coefficients away from the variable you want to isolate.
The goal of substitution is to make it easier to solve for a variable. For example, if you have $y=3x+4\\ x+y=8$ You can substitute $3x+4$ for $y$ to create an equation with only the variable $x$. $x+(3x+4)=8$ Now, you can simplify and solve for $x$.
In a matching problem, you can check to see if the solutions work in each equation by plugging in the $x$ and $y$ values to simplify. A point is a solution to a system if the point makes both equations true (left side equals right side after simplifying, i.e. $3=3$).
SolutionWhen solving a system of linear equations by substitution always check to see if one of the equations has an isolated variable, if not, then isolate a variable in one of the equations. Once you have an isolated variable you can follow the same steps each time.
$~$
Steps to solve: $y=2x+1 \\ y=3x-4$
- First, both of the equations have an isolated variable, so we are ready to begin the substitution method.
- Substitute $y=2x+1$ into $y$ in the second equation, resulting in $2x+1=3x-4$
- Now, solve for $x$:
- Now that you have $x=5$, substitute $5$ for $x$ into the first equation: $y=2x+1$.
- So, we have $x=5$ and $y=11$
- Finally, check to see if $x=5$ and $y=11$ works in the second equation as well:
- Therefore, the solution is $(5,11)$
Steps to solve: $2x+y=6 \\ y=4x$
- First, one of the equations has an isolated variable, so we are ready to begin the substitution method.
- Substitute $y=4x$ into $y$ in the first equation, resulting in $2x+(4x)=6$
- Now, solve for $x$:
- Now that you have $x=1$, substitute $1$ for $x$ into the second equation: $y=4x$.
- So, we have $x=1$ and $y=4$
- Finally, check to see if $x=1$ and $y=4$ works in the first equation as well:
- Therefore, the solution is $(1,4)$
Steps to solve: $x + y =3 \\ 2x - y = 6$
- First, neither of the equations have a variable isolated, so the first step is to isolate any variable. Let's isolate the $x$ in the first equation by subtracting $y$ on both sides.
- Substitute $x=3-y$ into $x$ in the second equation, resulting in $2(3-y)+y=6$
- Now, simplify and solve for $y$:
- Now that you have $y=0$, substitute $0$ for $y$ into the first equation: $x+y=3$.
- So, we have $x=3$ and $y=0$
- Finally, check to see if $x=3$ and $y=0$ works in the second equation as well:
- Therefore, the solution is $(3,0)$
Steps to solve: $y=5x-6 \\ x=2$
- First, both of the equations have an isolated variable, so we are ready to begin the substitution method. Also notice that the second equation identifies the value of $x$ as $2$. This means that on the line $x=2$, every point has an $x$-value of $2$.
- Substitute $2$ for $x$ into the first equation: $y=5x-6$.
- So, we have $x=2$ and $y=4$
- Finally, check to see if $x=2$ and $y=4$ works in the second equation as well:
- Therefore, the solution is $(2,4)$
-
Determine the solution for the system of equations using the substitution method.
HintsCheck to see if there is an equation in the system that has one of the variables isolated. If not, pick one equation and solve for either the $x$ or $y$ variable.
Substitute the value for the isolated variable into the other equation to create an equation with only $x$ or $y$.
Once you solve for a variable, don't stop there! A solution to a system is the point $(x,y)$, make sure you find the value of both variables.
Solution1.) To solve the system:
$2x+3y=7 \\ y=5x-9 $
First, substitute $5x-9$ into the first equation for $y$ to get $2x+3(5x-9)=7$.
Then simplify by distributing and combining like terms.
$2x+15x-27=7 \\ 17x-27=7 $
Now solve for $x$.
$\begin{array}{rcl} 17x-27&=&7 \\ \color{#669900}{+27} & &\color{#669900}{+27}\\ 17x&=&34 \\ \color{#669900}{\div17} & & \color{#669900}{\div17}\\ x &=& 2 \\ \end{array}$
Substitute $x=2$ into the second equation, $y=5x-9$.
$y=5(2)-9 \\ y=10 - 9 \\ y=1 $
Finally check to make sure $x=2$ and $y=1$ work in the first equation as well.
$2(2)+3(1)=7 \\ 4+3=7 \\ 7=7 ✓ $
Therefore the solution to this system is $(2,1)$.
$~$
2.) To solve the system:
$x=6y-4 \\ x-7y=-2 $
First, substitute $6y-4$ into the second equation for $x$ to get $(6y-4)-7y=-2$.
Then simplify by combining like terms.
$6y-4-7y=-2 \\ -4-y=-2 $
Now solve for $y$.
$\begin{array}{rcl} -4-y&=&-2 \\ \color{#669900}{+4} & &\color{#669900}{+4}\\ -y&=&2 \\ \color{#669900}{\div-1} & & \color{#669900}{\div-1}\\ y &=& -2 \\ \end{array}$
Substitute $y=-2$ into the first equation, $x=6y-4$.
$x=6(-2)-4 \\ x=-12 - 4 \\ x=-16 $
Finally check to make sure $x=-16$ and $y=-2$ work in the second equation as well.
$(-16)-7(-2)=-2 \\ -16 + 14 = -2 \\ -2=-2 ✓ $
Therefore the solution to this system is $(-16,-2)$.
$~$
3.) To solve the system:
$y=-3x-5 \\ y=2x + 10 $
First, substitute $2x + 10$ into the first equation for $y$ to get $2x + 10 = -3x - 5$.
Now solve for $x$.
$\begin{array}{rcl} 2x + 10 &=& -3x - 5 \\ \color{#669900}{+3x} & &\color{#669900}{+3x}\\ 5x + 10&=&-5 \\ \color{#669900}{-10} & &\color{#669900}{-10}\\ 5x &=& -15 \\ \color{#669900}{\div5} & & \color{#669900}{\div5}\\ x &=& -3 \\ \end{array}$
Substitute $x=-3$ into the second equation, $y=2x + 10$.
$y=2(-3)+10 \\ y=-6 + 10 \\ y=4 $
Finally check to make sure $x=-3$ and $y=4$ work in the first equation as well.
$4 = -3(-3)-5 \\ 4=9-5 \\ 4=4 ✓ $
Therefore the solution to this system is $(-3,4)$.
$~$
4.) To solve the system:
$x+5y=7 \\ 3x+y=-7 $
First notice that neither of the equations have a variable isolated. To isolate $x$ in the first equation, subtract $5y$ from both sides.
$\begin{array}{rcl} x+5y&=&7 \\ \color{#669900}{-5y} & &\color{#669900}{-5y}\\ x&=& 7-5y \\ \end{array}$
Now, substitute $7-5y$ into the second equation for $x$ to get $3(7-5y)+y=-7$.
Then simplify by distributing and combining like terms.
$21-15y+y=-7 \\ 21-14y=-7 $
Now solve for $y$.
$\begin{array}{rcl} 21-14y&=&-7 \\ \color{#669900}{-21} & &\color{#669900}{-21}\\ -147&=&-28 \\ \color{#669900}{\div-14} & & \color{#669900}{\div-14}\\ y &=& 2 \\ \end{array}$
Substitute $y=2$ into the first equation, $x+5y=7$ and solve for $x$.
$\begin{array}{rcl} x+5(2)&=&7 \\ x+10&=&7 \\ \color{#669900}{-10} & &\color{#669900}{-10}\\ x&=&-3 \\ \end{array}$
Finally check to make sure $x=-3$ and $y=2$ work in the second equation as well. $3(-3)+(2)=-7\\ -9+2=-7 \\ -7=-7 ✓ $
Therefore the solution to this system is $(-3,2)$.
-
Solve these word problems through systems of linear equations.
HintsCreate two equations based on the word problem. Find the two sentences that describe the situation and write an equation for each sentence.
For example: Sanja scored a total of 7 two- and three- point baskets in her game yesterday. She scored $17$ points for her team. How many three point baskets did Sanja score?
To write the system of equations, look at the first sentence: Sanja scored a total of 7 two- and three- point baskets. Let $x=$ the number of two-point baskets and $y=$ the number of three point baskets. The equation for this sentence is: $x+y=7$. To write the second equation, look at the second sentence: She scored $17$ points. Each two-point basket is worth two points and each three-point basket is worth three points, so the equation is $2x+3y=17$.
That gives a system to solve of:
$x+y=7 \\ 2x+3y=17$
Follow the steps to solve a system of linear equations by substitution:
- isolate a variable
- substitute into the other equation
- simplify and solve
- substitute in the known variable
- simplify
- check your work
Solution1.) In this word problem Jake has two pools and you are asked to determine when the pools will have the same amount of water.
Before you write an equation you must identify the variables. We can let $x=$time in minutes, and $y=$the total amount of water in the pool.
The first pool fills at a rate of 4 gallons per minute, that will be the rate ($4x$,) and starts empty, so the starting point is $0$. The equation for the first pool is $y=4x+0$, so $y=4x$.
The second pool fills at a rate of 3 gallons per minute, so the rate of change is $3x$, and starts with $20$ gallons already in the pool, so that starting point is $20$. The equation for the second pool is $y=3x+20$.
The question asks us to determine the number of minutes it will take for the two pools to have the same amount of water, we defined $x$ to be time in minutes, so we need to solve for $x$.
Now solve the system:
$y=4x \\ y=3x + 20 $
First, substitute $4x$ into the second equation for $y$, the solve for $x$.
$\begin{array}{rcl} 4x &=& 3x + 20 \\ \color{#669900}{-3x} & &\color{#669900}{-3x}\\ x&=&20 \\ \end{array}$
Therefore, the pools will have the same amount of water after $20$ minutes.
$~$
2.) In this word problem Amber is weighing two different combinations of Apples and Oranges.
Let's start by defining the variables. Let $x=$ the weight of one apple and $y=$ the weight of one orange.
The first combination has three apples and two oranges weighing $21$ ounces. The weight of three apples can be represented by $3x$ and the weight of two oranges can be represented by $2y$. Since the total weight of this combination is $21$ ounces, the equation for this combination is $3x + 2y=21$.
The second combination has one apple and four oranges weight $17$ ounces. The weight of one apple can be represented by $x$ and the weight of four oranges can be represented by $4y$. Since the total weight of this combination is $17$ ounces, the equation is $x+4y=17$.
Now solve the system:
$3x+2y=21 \\ x + 4y = 17$
First, isolate a variable in one of the equations. Since the second equation has a variable, $x$, with a coefficient of one, lets isolate the $x$ in $x+4y=17$:
$\begin{array}{rcl} x+4y&=&17 \\ \color{#669900}{-4y} & &\color{#669900}{-4y}\\ x&=&17-4y \\ \end{array}$
Now, substitute $17-4y$ for $x$ in the first equation. $3(17-4y)+2y=21$, then simplify and solve for y.
$\begin{array}{rcl} 51-12y+2y&=&21 \\ 51-10y&=&21 \\ \color{#669900}{-51} & &\color{#669900}{-51}\\ -10y &=& -30 \\ \color{#669900}{\div-10} & &\color{#669900}{\div-10}\\ y&=&3 \\ \end{array}$
The question asked how much one orange weighed, in the beginning of the problem we defined the weight of an orange to be the variable $y$. Since we solve the system to find $y=3$, then the weight of one orange is $3$ ounces.
It also asks for the weight of one apple. So, let's substitute $y=3$ into the second original equation, $x+4y=17$.
$\begin{array}{rcl} x+4y&=&17 \\ x+4(3)&=&17 \\ x+12&=&17 \\ \color{#669900}{-12} & &\color{#669900}{-12}\\ x&=&17-12 \\ x&=&5 \\ \end{array}$
Therefore, an apple weights $5$ ounces. $~$
3.) In this word problem Jen and Beth are comparing the number of songs they have on their digital music players.
Let's define $x$ to be the number of songs Jen has and $y$ to be the number of songs Beth has.
We are given that Jen has $28$ more songs on her digital music player than Beth has. So, Jen's songs are equal to Beth's songs plus 28. We can represent that by $x=y+28$.
Together they have 214 songs. That means that Jen's songs plus Beth's songs equal 214. This can be represented by $x+y=214&.
To solve this system:
$ x=y+28 \\ x+y=214$
First, substitute $y+28$ for $x$ to get $(y+28)+y=214$. Then, combine like terms and solve for $y$.
$\begin{array}{rcl} y+28+y&=&214 \\ 2y+28&=&214 \\ \color{#669900}{-28} & &\color{#669900}{-28}\\ 2y &=& 186 \\ \color{#669900}{\div2} & &\color{#669900}{\div2}\\ y&=&93 \\ \end{array}$
At the start of the problem we defined $y$ to be the number of songs Beth has, so Beth has $93$ songs. The question also asks us how many songs Jen has, so we need to substitute $93$ for $y$ in the equation $x=y+28$.
$x=93+28\\ x=121$
Therefore, Jen has $121$ songs on her digital music player.
-
Solve the equation by substituting.
HintsSubstitute in the given value of $y$ into the first equation.
After substituting, simplify and solve for $x$.
For example, given $\begin{array}{rcl} 2x+3y&=&15 \\ y&=&1\\ \end{array}$
Start but substituting $1$ for $y$ into the first equation, then simplify and solve for x.
$\begin{array}{rcl} 2x+3(1)&=&15 \\ 2x+3&=&15\\ \color{#669900}{-3} & & \color{#669900}{-3}\\ 2x&=&12\\ \color{#669900}{\div2} & & \color{#669900}{\div2}\\ x&=&6\\ \end{array}$
SolutionWhen a value for $x$ or $y$ is given, you automatically know one of the values in the solution $(x,y)$. To find the other value, substitute in the known value into the equation with two variables.
1) To solve :
$\begin{array}{rcl} y+5&=&3x \\ y&=&7\\ \end{array}$
First, substitute $y=7$ into the first equation, then simplify and solve for $x$:
$\begin{array}{rcl} 7+5&=&3x \\ 12&=&3x\\ \color{#669900}{\div3} & & \color{#669900}{\div3}\\ 4&=&x \\ \end{array}$
Therefore, the solution to the system is $x=4$ and $y=7$, written as a coordinate point is $(4,7)$.
$~$
2) To solve:
$\begin{array}{rcl} y-2x&=&3 \\ y&=&-5\\ \end{array}$
First, substitute $y=-5$ into the first equation, then simplify and solve for $x$:
$\begin{array}{rcl} (-5)-2x&=&3 \\ -5-2x&=&3\\ \color{#669900}{+5} & & \color{#669900}{+5}\\ -2x&=&8 \\ \color{#669900}{\div-2} & & \color{#669900}{\div-2}\\ x&=&-4 \\ \end{array}$
Therefore, the solution to the system is $x=-4$ and $y=-5$, written as a coordinate point is $(-4,-5)$.
$~$
3) To solve:
$\begin{array}{rcl} 6x+5y&=&28 \\ y&=&2\\ \end{array}$
First, substitute $y=2$ into the first equation, then simplify and solve for $x$:
$\begin{array}{rcl} 6x+5(2)&=&28 \\ 6x+10&=&28\\ \color{#669900}{-10} & & \color{#669900}{-10}\\ 6x&=&18 \\ \color{#669900}{\div6} & & \color{#669900}{\div6}\\ x&=&3 \\ \end{array}$
Therefore, the solution to the system is $x=3$ and $y=2$, written as a coordinate point is $(3,2)$.
-
Solve systems of linear equations with fractional coefficients.
HintsAt least one equation should have a variable isolated.
Remember the rules for multiplying fractions by constants: numerator multiplied by the constant, then divide by the denominator.
A solutions is (x,y), don't forget to solve for both x and y.
Solution1.) To Solve
$ y= \frac{1}{2}x + 3\\ \frac {1}{2}x + 3y = 1 $
Substitute $\frac {1}{2}x + 3$ for $y$ in the second equation to get $\frac{1}{2}x + 3(\frac{1}{2}x + 3) =1$.
Simplify and solve for $x$
$\begin{array}{rcl} \frac{1}{2}x + 3(\frac {1}{2}x + 3) &=& 1 \\ \frac{1}{2}x + \frac {3}{2}x + 9 &=& 1 \\ \frac{4}{2}x + 9 &=& 1 \\ 2x + 9 &=& 1 \\ \color{#669900}{-9} & &\color{#669900}{-9}\\ 2x &=& -8 \\ \color{#669900}{\div2} & & \color{#669900}{\div2}\\ x &=& -4 \\ \end{array}$
Substitute $x=-4$ into the first equation to solve for $y$.
$y= \frac {1}{2}x + 3 \\ y= \frac {1}{2} (-4) + 3 \\ y= -2 + 3 \\ y = 1 $
Check to see if $x=-4$ and $y=1$ works in the second equation as well.
$ \frac{1}{2}x + 3y = 1 \\ \frac{1}{2}(-4) + 3(1) = 1 \\ -2 + 3 = 1 \\ 1 = 1 ✓ $
Therefore, the solution to the system is $(-4, 1)$
$~$
2.) To Solve
$ x= \frac {-3}{2}y + 6\\ 4x - 3y = 24 $
Substitute $ \frac{-3}{2}y + 6$ for $x$ in the second equation to get $4(\frac{-3}{2}y + 6) - 3y = 24$.
Simplify and solve for $y$
$\begin{array}{rcl} 4(\frac{-3}{2}y + 6) - 3y &=& 24 \\ \frac {-12}{2}y + 24 - 3y &=& 24 \\ -6y + 24 - 3y &=& 24 \\ -9y + 24 &=& 24\\ \color{#669900}{-24} & &\color{#669900}{-24}\\ -9y &=& 0 \\ \color{#669900}{\div-9} & & \color{#669900}{\div-9}\\ y &=& 0 \\ \end{array}$
Substitute $y=0$ into the first equation to solve for $x$.
$ x= \frac{-3}{2}y + 6 \\ x= \frac{-3}{2}(0) + 6 \\ x = 0 + 6 \\ x= 6 $
Check to see if $x=6$ and $y=0$ works in the second equation as well.
$ 4x - 3y = 24 \\ 4(6) - 3(0) = 24 \\ 24 - 0 = 24 \\ 24 = 24 ✓ $
Therefore, the solution to the system is $(6, 0)$.
$~$
3.) To solve
$ 5y = 3x + 5 \\ \frac{4}{5} x + 2y = 12 $
Isolate a variable in one of the equations. Let's isolate $y$ in the first equation by dividing both sides by $5$.
$\begin{array}{rcl} 5y &=& 3x + 5 \\ \color{#669900}{\div5} & & \color{#669900}{\div5}\\ y &=& \frac {3}{5} x + 1 \\ \end{array}$
Substitute $\frac{3}{5} x + 1 $ for $y$ in the second equation.
$\begin{array}{rcl} \\ \frac { 4 }{ 5 } x + 2(\frac { 3 }{ 5 } x + 1) &=& 12 \\ \frac { 4 }{ 5 } x + \frac { 6 }{ 5 } x + 2 &=& 12 \\ \frac { 10 }{ 5 } x + 2 &=& 12 \\ 2x + 2 &=& 12 \\ \color{#669900}{-2} & &\color{#669900}{-2}\\ 2x &=& 10 \\ \color{#669900}{\div2} & &\color{#669900}{\div2}\\ x &=& 5 \\ \end{array}$
Substitute $x=5$ into the first equation to solve for $y$
$\begin{array}{rcl} \\ 5y &=& 3x + 5 \\ 5y &=& 3(5) + 5 \\ 5y &=& 15 + 5 \\ 5y &=& 20 \\ \color{#669900}{\div5} & &\color{#669900}{\div5}\\ y &=& 4 \\ \end{array}$
Check to see if $x=5$ and $y=4$ works in the second equation as well.
$ \frac { 4 }{ 5 } x + 2y = 12 \\ \frac { 4 }{ 5 } (5) + 2(4) = 12 \\ \frac { 20 }{ 5 } + 8 = 12\\ 4 + 8 = 12\\ 12 = 12 ✓ $
Therefore the solution is $(5,4)$
$~$
4.) To Solve
$ y = \frac { 3 }{ 4 } x + 6 \\ y = \frac { 7 }{ 4 } x + 2 $
Substitute $ \frac { 7 }{ 4 } x + 2$ for $y$ in the first equation to get $\frac { 7 }{ 4 } x + 2 = \frac { 3 }{ 4 } x + 6 $.
Simplify and solve for $x$
$\begin{array}{rcl} \frac { 7 }{ 4 } x + 2 &=& \frac { 3 }{ 4 } x + 6 \\ \color{#669900}{-\frac { 3 }{ 4 } x} & &\color{#669900}{-\frac { 3 }{ 4 } x}\\ \frac { 4 }{ 4 } x + 2 &=& 6 \\ x + 2 &=& 6 \\ \color{#669900}{-2} & & \color{#669900}{-2}\\ x &=& 4 \\ \end{array}$
Substitute $x=4$ into the first equation to solve for $y$.
$y= \frac { 3 }{ 4 } x + 6 \\ y= \frac { 3 }{ 4 } (4) + 6 \\ y= \frac { 12 }{ 4 } + 6 \\ y = 3 +6 \\ y = 9 $
Check to see if $x=4$ and $y=9$ works in the second equation as well.
$ y = \frac { 7 }{ 4 } x + 2 \\ (9) = \frac { 7 }{ 4 } (4) + 2 \\ 9 = \frac { 28 }{ 4 } + 2 \\ 9 = 7 + 2 \\ 9 = 9 ✓ $
Therefore, the solution to the system is $(4, 9)$.