Using and Understanding the Discriminant
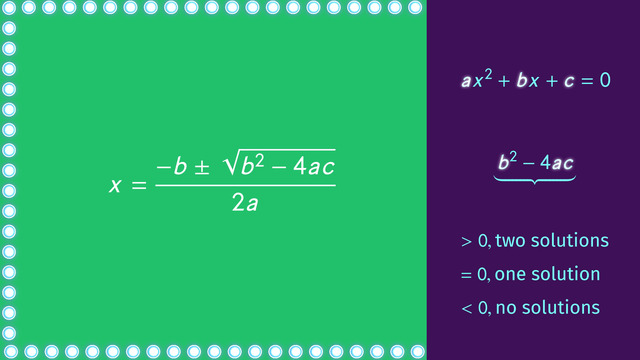

Basics on the topic Using and Understanding the Discriminant
A quadratic equation in standard form ax² + bx + c = 0 can be solved in various ways. These include factoring, completing the square, graphing, and using the quadratic formula. Solving for the roots or solutions of a quadratic equation by using the quadratic formula is often the most convenient way. The solutions to a quadratic equation can be determined by this quadratic formula: x = [-b ± √(b²-4ac)] / 2a. We can predict the number of solutions to a quadratic equation by evaluating the discriminant given by b²-4ac or the radicand expression in the quadratic formula. The value of the discriminant determines the nature and number of solutions of a quadratic equation.
If b²-4ac is positive, there will be two distinct, real solutions.
For example, the quadratic equation x² - 7x + 12 = 0 has two distinct, real solutions since b²-4ac = (-7)² - 4(1)(12) = 49 - 48 = 1 is positive.
If b²-4ac is zero, there will be one distinct, real solution.
For example, the quadratic equation 4x² - 4x + 1 = 0 has one distinct, real solution since b²-4ac = (-4)² - 4(4)(1) = 16 - 16 = 0.
If b2-4ac is negative, there are no real solutions.
For example, the quadratic equation 5x² + 2x + 3 = 0 has no real solutions since b2-4ac = (2)² - 4(5)(3) = 4 - 60 = -56 is negative.
Solve quadratic equations with real coefficients that have complex solutions.
CCSS.MATH.CONTENT.HSN.CN.C.7
Transcript Using and Understanding the Discriminant
”Hello! It's that time again for your favorite quiz show THE WALL OF FAME!” ”The first contestant on today's show is Theresa! I hope you're ready to play THE WALL OF FAME!” Before we begin today's game, let's quickly review our game rules. Theresa, you're about to see today's wall. On the wall are 5 secret doors with one equation written over each door. During the game, you will get to open 3 of those doors. For each door you pick, you will receive a prize equal to the number of solutions the equation has. If each door you pick reveals a prize, you get to come back on the show tomorrow for a chance to win an even bigger prize!
Understanding the Discriminant
The secret to this game is understanding and using the discriminant. If Theresa can figure out how to use this tool, she just might have a chance to win all the prizes and come back tomorrow! Let's take a look at today's WALL OF FAME! The equations we have today are:
Equation 1: x-squared minus 10x plus 34.
Equation 2: 3 x-squared minus 4x plus 10.
Equation 3: x-squared minus 3x plus 5.
Equation 4: x-squared plus 2 root 2x plus 2.
Equation 5: x-squared plus 6x minus 16.
With her first choice, Theresa picks door number 4. Remember, we said we could use the discriminant to quickly determine whether or not Theresa has won one of our fabulous prizes. The discriminant comes from the quadratic formula, and it's formula is b-squared minus 4ac where a, b and c refer to the coefficients and constant of a quadratic equation in standard form.
When the discriminant is positive, our equation will have 2 solutions; when the discriminant is equal to 0, our equation has 1 solution and when our discriminant is negative, our equation will have no solutions. Let's take a look at the equation Theresa has just selected. In the equation Theresa has just selected, "a" is equal to 1, "b" is equal to 2 times the square root of 2, and "c" is equal to 2.
Let's calculate the discriminant! The quantity 2 times the square root of 2 squared will be 8. 8 minus 8 will equal 0. Because the discriminant is equal to 0, this equation will have 1 solution. Theresa, you've just won 1 brand new unicorn! Doesn't she look happy?! That's about as good of a start as you can ask for!
Second Example
With her second selection, Theresa picks the fifth equation. Let's take a closer look! In this equation, "a" is equal to 1, "b" is equal to 6, and "c" is equal to negative 16. Let's calculate the discriminant! Plugging in our values, we get 6 squared minus 4 times 1 times negative 16.
Using PEMDAS, we get 36 plus 64 which equals 100. Wow! Look at that! Theresa has just won a pair of Positron and Negatron figurines! 2 prizes for an equation with 2 solutions! Theresa's doing great so far! If she can pick a door with one more prize she'll be invited back for tomorrow's show and a chance to win the Grand Prize!
And with her final selection, Theresa picks the equation on door number 2! Let's take a look at her equation! In this equation, "a" is equal to 3, "b" is equal to negative 4, and "c" is equal to 10. Let's calculate the discriminant! Plugging in our values, we get negative 4 squared minus 4 times 3 times 10. Calculating our math, we get 16 minus 120 which equals negative 104. What do you think this means? Not only for how many solutions our equation has but for Theresa's chances at coming back tomorrow?
Summary
Remember, when our discriminant is greater than 0 that means our equation will have 2 solutions. When our discriminant is equal to 0 our equation will have 1 solution. And when our discriminant is negative, our equation will have no real solutions.
Well Folks! That also means there's no prize! Although Theresa is going to be disappointed, at least she got some action figures and a new Unicorn! Although that Unicorn looks a bit suspicious... And the host's hair looks a bit suspicious too!
Using and Understanding the Discriminant exercise
-
Define the discriminant.
HintsThe discriminant could be found for this equation:
$2x^2-7x+10$
What type of equation is this, and what form is it in?
A quadratic equation can have zero, one, or two solutions.
SolutionThe discriminant is a mathematical expression that can be calculated for quadratic equations in standard form. Therefore the equation will be in the form:
$ax^2+bx+c=0$
The discriminant is equal to $b^2-4ac$.
The discriminant is useful because it tells you the number of solutions, or roots, that a quadratic equation has. If the discriminant is positive, the equation has two solutions. If it is equal to zero, the equation has one solution. If it is negative, the equation has zero solutions.
-
Determine the number of solutions.
HintsThe discriminant is equal to:
$b^2-4ac$
If the discriminant is positive, the equation has two solutions. If it is equal to zero, the equation has one solution. If it is negative, the equation has zero solutions.
SolutionTheresa sees that she has a quadratic equation in standard form. She knows that she can use the discriminant to find the number of solutions to the equation.
She knows that the discriminant is equal to:
$b^2-4ac$
She substitutes in the values from the given equation, and gets:
$(2 \sqrt2)^2-4(1)(2)$
Using PEMDAS, she finds the discriminant to be equal to $0$.
She knows that if the discriminant is positive, the equation has two solutions. If it is equal to zero, the equation has one solution. If it is negative, the equation has zero solutions.
Since the discriminant is equal to zero, Theresa can see that this equation has one solution, and she should get one prize by opening this door.
-
Find the discriminants.
HintsPay close attention to signs.
Remember that the standard form of a quadratic equation is:
$a x^2 + b x + c = 0$
For the standard form of a quadratic equation, the discriminant is equal to:
$b^2 - 4(a)(c)$
SolutionEach quadratic equation is given in the standard form:
$a x^2 + b x + c = 0$
For the standard form of a quadratic equation, the discriminant is equal to:
$b^2 - 4(a)(c)$
We can therefore determine the values of $a$, $b$, and $c$, and use these values to find the expression for the discriminant.
From the equation:
$2 x^2 -5 x + 6 = 0$
We can see that:
$a = 2$
$b = -5$
$c = 6$
And therefore we can determine that the discriminant is equal to:
$(-5)^2 - 4(2)(6)$
Similarly, the other quadratic equations can be paired with their corresponding discriminants.
For $4 x^2 + 4 x + 1 = 0$ the discriminant is: $4^2 - 4(4)(1)$
For $5 x^2 + 3 x -7 = 0$ the discriminant is: $3^2 - 4(5)(-7)$
For $3 x^2 + 8 x + 5 = 0$ the discriminant is: $8^2 - 4(3)(5)$
For $-2 x^2 -3 x -4 = 0$ the discriminant is: $(-3)^2 - 4(-2)(-4)$
-
Determine which equation has two solutions.
HintsYou can use the discriminant to check how many solutions there are to each equation.
If the discriminant is positive, the equation has two solutions.
The discriminant is equal to $b^2-4ac$.
SolutionThe equations above the doors are all standard form quadratic equations. Therefore John can use the discriminant to check how many solutions each equation has.
If the discriminant is positive, the equation has two solutions. If it is equal to zero, the equation has one solution. If it is negative, the equation has zero solutions. Therefore John must find the equation whose determinant is positive.
John decides to evaluate the determinant for each quadratic equation. He begins with the equation:
$3 x^2 +2 x + 1 = 0$
He finds the determinant to be:
$(2)^2 - 4(3)(1) = -8$
The determinant for this equation is negative. Therefore this is not the right door.
Similarly, for the other equations:
Door 2
$2 x^2 -4 x + 2 = 0$
The determinant is:
$(-4)^2 - 4(2)(2) = 0$
The determinant for this equation is zero. Therefore this is not the right door.
Door 3
$2 x^2 + 3 x +5 = 0$
The determinant is:
$(3)^2 - 4(2)(5) = -31$
The determinant for this equation is negative. Therefore this is not the right door.
Door 4
$- x^2 + 2 x + -1 = 0$
The determinant is:
$(2)^2 - 4(-1)(-1) = 0$
The determinant for this equation is zero. Therefore this is not the right door.
Door 5
$2 x^2 -6 x +3 = 0$
The determinant is:
$(-6)^2 - 4(2)(3) = 12$
The determinant for this equation is positive. Therefore this is the right door.
-
Explain what a discriminant equal to $100$ tells you.
HintsA quadratic equation can have zero, one, or two solutions.
If the discriminant is equal to zero, the equation has one solution.
If the discriminant is negative, the equation has zero solutions.
SolutionThe discriminant is useful because it tells you the number of solutions, or roots, that a quadratic equation has. If the discriminant is positive, the equation has two solutions. If it is equal to zero, the equation has one solution. If it is negative, the equation has zero solutions.
In this case, the discriminant is equal to $100$, and is positive. Therefore this equation has two solutions.
-
Calculate the discriminant.
HintsPay close attention to signs in your calculations.
Remember that you can determine how many solutions an equation has by comparing the discriminant to zero.
Remember that a quadratic equation can only have $0$, $1$, or $2$ solutions.
SolutionIris knows that the discriminant can be found for the standard form of a quadratic equation using the equation:
$b^2-4ac$
She also knows that if the discriminant is positive, the equation has two solutions. If it is equal to zero, the equation has one solution. If it is negative, the equation has zero solutions.
For the first equation:
$-x^2 + 3x -4 =0$
She evaluates the discriminant:
$3^2-4(-1)(-4)$
$= 9 - 16$
$= -7$
Since the discriminant is negative, the equation has $0$ solutions.
Similarly, for the other equations:
For the equation $-2x^2 +x +1 =0$ she finds that the discriminant is $9$. Therefore the equation has $2$ solutions.
For the equation $8x^2 + 6x +2 =0$ she finds that the discriminant is $0$. Therefore the equation has $1$ solution.
For the equation $7x^2 + 5x -3 =0$ she finds that the discriminant is $109$. Therefore the equation has $2$ solutions.
What are Quadratic Functions?
Graphing Quadratic Functions
FOILing and Explanation for FOIL

Solving Quadratic Equations by Taking Square Roots
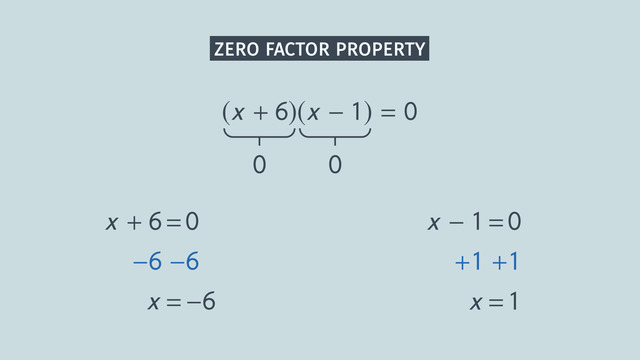
Solving Quadratic Equations by Factoring
Factoring with Grouping

Solving Quadratic Equations Using the Quadratic Formula

Solving Quadratic Equations by Completing the Square
Finding the Value that Completes the Square
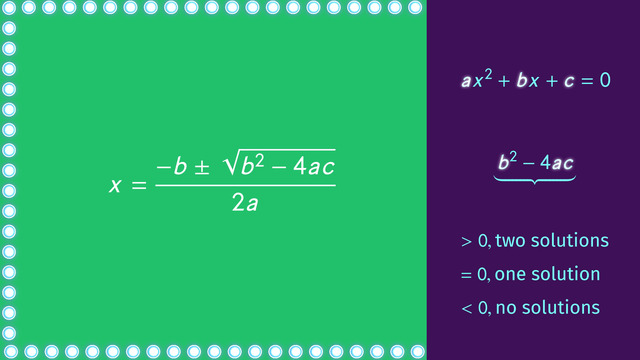
Using and Understanding the Discriminant
Word Problems with Quadratic Equations











