Solving Quadratic Equations Using the Quadratic Formula


Basics on the topic Solving Quadratic Equations Using the Quadratic Formula
Summary of Solving Quadratic Equations Using the Quadratic Formula
One way of solving quadratic equations of the form ax² + bx + c = 0 is by using the quadratic formula.
The quadratic formula states that x = { [-b ± sqrt ( b² – 4ac)] / 2a] } , where a, b, and c are the coefficients of the quadratic equation (with a, b, and c being real numbers, and a ≠ 0).
For example, given the quadratic equation x² – 5x + 6 = 0, first identify the values of a, b, and c. The given equation has a = 1, b = -5, and c = 6. After identifying the values of a, b, and c, substitute these values into the quadratic formula. So, we get x = { 5 ± sqrt( (-5)² = 4(1)(6)) / 2(1)]}.
Simplifying the formula by using PEMDAS, we get that x = 2 and 3. You can check if the solutions are correct by substituting them into the quadratic equation. Once they satisfy the equation or the result is true, then the solutions are correct.
Sometimes a quadratic equation has two solutions, exactly one solution, or has imaginary solutions. However, these solutions don’t always satisfy a given quadratic problem. These solutions are called extraneous solutions. Therefore, it is necessary to always check the solutions in order to get the correct one.
Solve quadratic equations in one variable.
Common Core Reference
CCSS.MATH.CONTENT.HSA.REI.B.4.B
Let's practice: quadratic formula equation Exercises
With the following exercises on the topic of quadratic formula equation, you can test whether you have understood everything. Test your knowledge now!
Transcript Solving Quadratic Equations Using the Quadratic Formula
Eddie is really smart, and he likes to use his 'smarts' to play pranks. His latest invention is a machine he can use to launch water balloons.
Quadratic formula
By solving quadratic equations with the quadratic formula, Eddie can figure out even the most unruly quadratic equations. All Eddie has to do to launch water balloons, is choose the values for ‘a,’ ‘b,’ and ‘c,’ and then he can watch the balloons fly in a perfectly-shaped parabola. From the shape of the flight path, you probably guessed that the corresponding equation is quadratic.
The machine uses factoring to calculate the solution set, or the roots, of quadratic equations. So, Eddie can figure out where it will land. Oh no! Eddie’s pet guinea pig just ran across the control panel and accidentally entered values for 'a', 'b,' and 'c' and now the machine is activating the cannon. Even worse, the machine can’t find a solution by factoring the equation, so who knows where this wet missile will land?!
Maybe Eddie can stop the launch by unplugging the machine but he’s too late – the machine fired. Uh oh! Where’s his guinea pig? Eddie's pet must have crawled into the cannon and launched with the water balloon! Eddie has got to get his guinea pig back, but if the machine can’t find a solution by factoring the quadratic equation, what can he do? How will he know where his furry little friend landed?
Hey, whats's that? Super Quadratic Formula Man, SQFM for short, heard Eddie's cries and has come to the rescue. When factoring and completing the square won’t do the job, SQFM and his quadratic formula can save the day.
Calculating the quadratic formula
To practice using the quadratic formula, we'll use an equation where we already know the solution set -- the same one Eddie's machine factored earlier. Remember to manipulate the quadratic equation so that it's equal to zero. That makes it easier to identify the coefficients ‘a,’ ‘b,’ and ’c.’ Now, insert the values for this equation into the formula: 'a' is equal to negative 1, 'b' is equal to negative 3, and 'c' is equal to 4, and then calculate the solution set. The solution set is exactly the same, negative 4 and 1! The quadratic formula works!
Finding the roots of the equation
Now we can use it to find the roots of the equation the machine choked on earlier: zero is equal to negative x-squared plus 30x minus 100, and then use the quadratic formula to find Eddie's friend. For this equation, 'a' is equal to negative 1, 'b' is equal to 30' and 'c' is equal to negative 100. Simplify and round to two decimal places, the solution set is 3.82 and 26.18. SQFM’s job is done.
Eddie uses the roots of the equation to locate his pet, but when he arrives at the calculated location, his furry friend is nowhere to be seen. I guess Eddie's not the only prankster in town!
Solving Quadratic Equations Using the Quadratic Formula exercise
-
Factor the quadratic equation.
HintsA standard quadratic equation is of the form $ax^2+bx+c=0$.
Pay attention to the signs of $a$, $b$, and $c$.
To factor any quadratic equation of the form $x^2+bx+c$, find the factors of $c$ which sum to $b$.
The zero factor property states that if any product equals zero then one of its factors must also equal zero.
SolutionTo factor the quadratic equation $-1x^2-3x+4=0$, we must first factor out $-1$ to get
$-1(x^2+3x-4)=-(x^2+3x-4)$.
Next we're looking for the factors of $-4$ which sum to $3$:
- $1\times (-4)=-4$ and $1-4=-3$ This pair doesn't work.
- $-1\times 4=-4$ and $-1+4=3$ $~~~~~$✓
$-x^2-3x+4=-(x^2+3x-4)=-(x+4)(x-1)$.
To solve the equation $-x^2-3x+4=0$ we can also solve $-(x+4)(x-1)=0$.
Using the zero factor property, we get either
$\begin{array}{rcl} x+4 & = & ~0\\ \color{#669900}{-4} & &\color{#669900}{-4}\\ x & = & ~-4 \end{array}$
or
$\begin{array}{rcl} x-1 & = & ~0\\ \color{#669900}{+1} & &\color{#669900}{+1}\\ x & = & ~1 \end{array}$
-
Use the quadratic formula to solve the equation.
Hints$ax^2+bx+c=0$ is the standard form of a quadratic equation.
You still have to put the values of $a$, $b$, and $c$ into the quadratic formula.
The first step is $x=\frac{-30\pm\sqrt{30^2-4(-1)(-100)}}{2(-1)}$.
SolutionIn the equation above we have $a=-1$, $b=30$ and $c=-100$.
We can use the quadratic formula to factor this equation. The quadratic formula is given by:
$x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}$
Plugging $a$, $b$, and $c$ into it gives us
$x=\frac{-30\pm\sqrt{30^2-4(-1)(-100)}}{2(-1)}$.
Next we simplify to get
$\begin{array}{rcl} x&=&~\frac{-30\pm\sqrt{30^2-4(-1)(-100)}}{2(-1)}\\ &=&~-\frac{-30\pm\sqrt{900-400}}{2}\\ &=&~-\frac{-30\pm\sqrt{500}}{2}\\ x_1&=&~-\frac{-30+\sqrt{500}}{2}\approx 3.82\\ x_2&=&~-\frac{-30-\sqrt{500}}{2}\approx26.18\\ \end{array}$
-
Find the value of $x$ which satisfies each quadratic equation.
HintsFirst identify $a$, $b$, and $c$.
$a$ is the coefficient of $x^2$, $b$ is the coefficient of $x$, and $c$ is the coefficient of $1$.
Pay attention to signs.
SolutionOnce you have identified $a$, $b$, and $c$ in the quadratic equation $ax^2+bax+c=0$, you can put these values into the quadratic formula:
$x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}$.
$~$
For $x^2+5x+4=0$ $\rightarrow$ $a=1$, $b=5$ and $c=4$
The solutions are given by
$x=\frac{-5\pm\sqrt{5^2-4(1)(4)}}{2(1)}$.
$~$
For $-x^2-4x+5=0$ $\rightarrow$ $a=-1$, $b=-4$ and $c=5$
The solutions are given by
$x=\frac{4\pm\sqrt{(-4)^2-4(-1)(5)}}{2(-1)}$.
$~$
For $2x^2-4x-16=0$ $\rightarrow$ $a=2$, $b=-4$ and $c=-16$
The solutions are given by
$x=\frac{4\pm\sqrt{(-4)^2-4(2)(-16)}}{2(-1)}$.
$~$
For $2x^2+8x-10=0$ $\rightarrow$ $a=2$, $b=8$ and $c=-10$
The solutions are given by
$x=\frac{-8\pm\sqrt{8^2-4(2)(-10)}}{2(2)}$.
-
Determine the path of the quadratic equation.
HintsFor $x^2+2x+1=0$, we have that $a=1$, $b=2$, and $c=1$.
Use the quadratic formula: $x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}$.
One solution is negative and the other one is positive.
SolutionWe have to solve the equation $-0.2x^2+x+10=0$ with $a=-0.2$, $b=1$ and $c=10$.
We put these values for $a$, $b$, and $c$ into the quadratic formula,
$x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}$,
to get
$x=\frac{-1\pm\sqrt{1^2-4(-0.2)(10)}}{2(-0.2)}$.
Then we simplify:
$\begin{array}{rcl} x&=&~\frac{-1\pm\sqrt{1^2-4(-0.2)(10)}}{2(-0.2)}\\ &=&~\frac{-1\pm\sqrt{1+8}}{-0.4}\\ &=&~-\frac{-1\pm\sqrt9}{0.4}\\ x_1&=&~-\frac{-1+3}{0.4}=-5\\ &=&~-\frac{-1-3}{0.4}=10 \end{array}$
We can graph these solutions as the $x$-intercepts of the graph of the quadratic equation, which will look like a downwards opened parabola (as $a<0$).
-
Identify the values of $a$, $b$, and $c$ for each quadratic equation.
HintsFor any quadratic equation $ax^2+bx+c=0$, keep the following in mind:
- $a$ is the coefficient of $x^2$
- $b$ is the coefficient of $x$
- $c$ is the coefficient of $1$
Pay attention to signs.
For $-3x^2+x+5=0$, we have:
- $a=-3$
- $b=1$
- $c=5$
SolutionLet's use the quadratic formula:
$x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}$.
To solve a quadratic equation $ax^2+bx+c=0$ using the quadratic formula, we must identify $a$, $b$, and $c$ in the corresponding equation:
- $a$ is the coefficient of $x^2$
- $b$ is the coefficient of $x$
- $c$ is the coefficient of $1$
Let's identify $a$, $b$, and $c$ for two examples:
$-1x^2+(-3)x+4=0$
- $a=-1$
- $b=-3$
- $c=4$
- $a=-1$
- $b=30$
- $c=-100$
-
Solve the given quadratic equations.
HintsYou find the solution of the first equation by simplifying $x=\frac{-5\pm\sqrt{5^2-4(1)(4)}}{2(1)}$.
You can also check the solutions by putting them into the original equation.
Keep track of the signs of the coefficients.
SolutionFirst determine $a$, $b$, and $c$ in the quadratic equation $ax^2+bx+c=0$.
Next put these values for $a$, $b$, and $c$ into the quadratic formula:
$x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}$.
$~$
Let's take a look at the quadratic equations we were asked to solve:
$x^2+5x+4=0$ with $a=1$, $b=5$ and $c=4$.
The solutions are given by
$\begin{array}{rcl} x&=&~\frac{-5\pm\sqrt{5^2-4(1)(4)}}{2(1)}\\ &=&~\frac{-5\pm\sqrt{25-16}}{2}\\ &=&~\frac{-5\pm\sqrt9}{2}\\ x_1&=&~\frac{-5+3}{2}=-1\\ x_2&=&~\frac{-5-3}{2}=-4 \end{array}$
$~$
$-x^2-4x+5=0$ with $a=-1$, $b=-4$ and $c=5$.
The solutions are given by
$\begin{array}{rcl} x&=&~\frac{4\pm\sqrt{(-4)^2-4(-1)(5)}}{2(-1)}\\ &=&~\frac{4\pm\sqrt{16+20}}{-2}\\ &=&~-\frac{4\pm\sqrt{36}}{2}\\ x_1&=&~-\frac{4+6}{2}=-5\\ x_2&=&~-\frac{4-6}{2}=1 \end{array}$
$~$
$2x^2-4x-16=0$ with $a=2$, $b=-4$ and $c=-16$.
The solutions are given by
$\begin{array}{rcl} x&=&~\frac{4\pm\sqrt{(-4)^2-4(2)(-16)}}{2(2)}\\ &=&~\frac{4\pm\sqrt{16+128}}{4}\\ &=&~\frac{4\pm\sqrt{144}}{4}\\ x_1&=&~\frac{4+12}{4}=4\\ &=&~\frac{4-12}{4}=-2 \end{array}$
$~$
$2x^2+8x+6=0$ $\rightarrow$ $a=2$, $b=8$ and $c=6$
The solutions are given by
$\begin{array}{rcl} x&=&~\frac{-8\pm\sqrt{8^2-4(2)(6)}}{2(2)}\\ &=&~\frac{-8\pm\sqrt{64-48}}{4}\\ &=&~\frac{-8\pm\sqrt{16}}{4}\\ x_1&=&~\frac{-8+4}{4}=-1\\ x_2&=&~\frac{-8-4}{4}=-3 \end{array}$
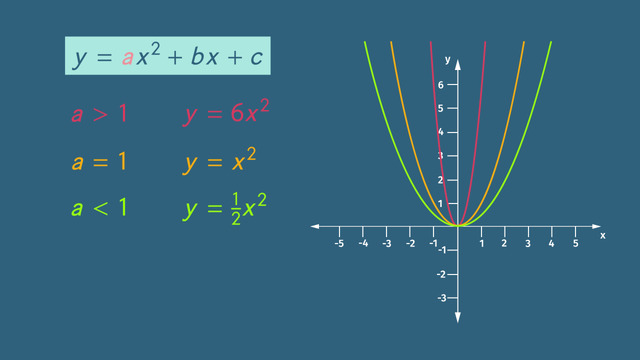
What are Quadratic Functions?
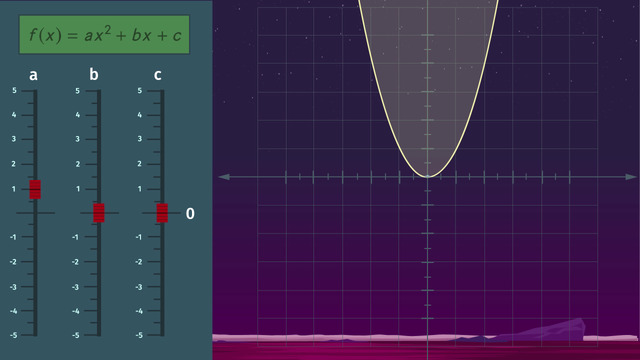
Graphing Quadratic Functions
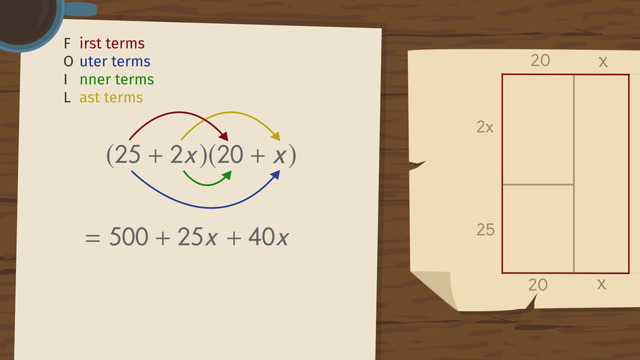
FOILing and Explanation for FOIL

Solving Quadratic Equations by Taking Square Roots
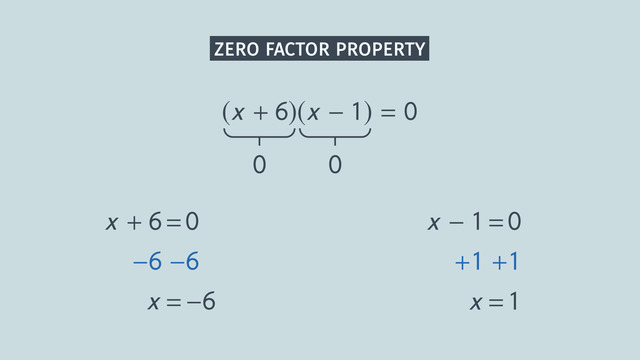
Solving Quadratic Equations by Factoring
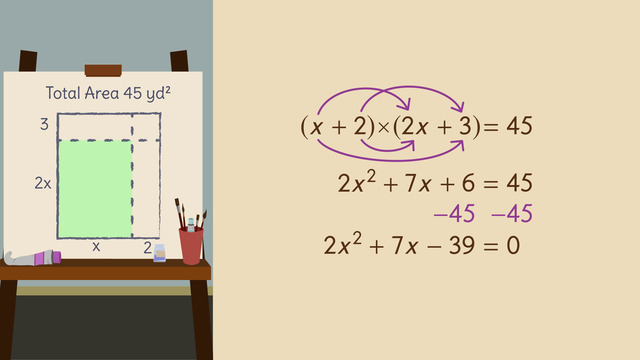
Factoring with Grouping

Solving Quadratic Equations Using the Quadratic Formula

Solving Quadratic Equations by Completing the Square
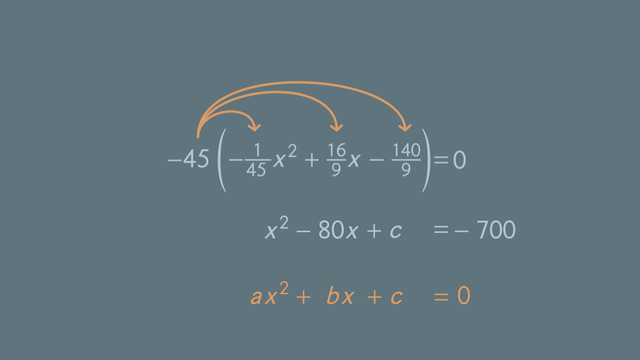
Finding the Value that Completes the Square
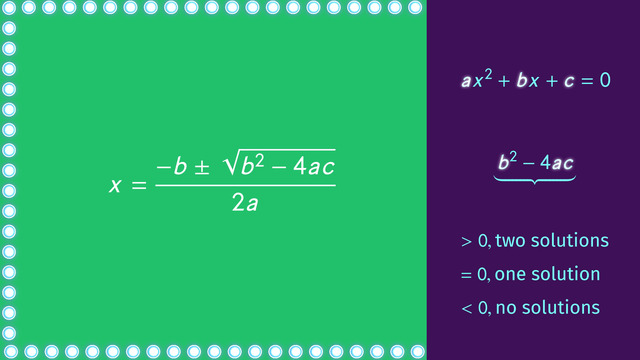
Using and Understanding the Discriminant
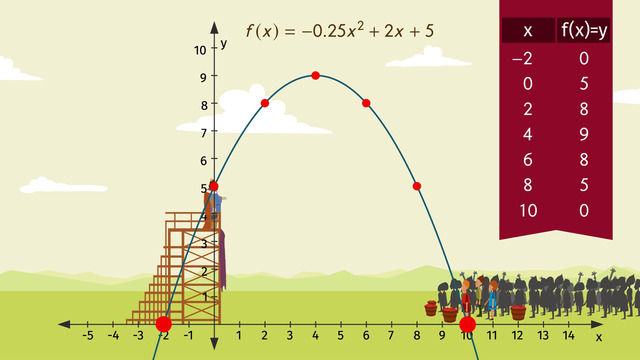
Word Problems with Quadratic Equations









