Solving Quadratic Equations by Factoring
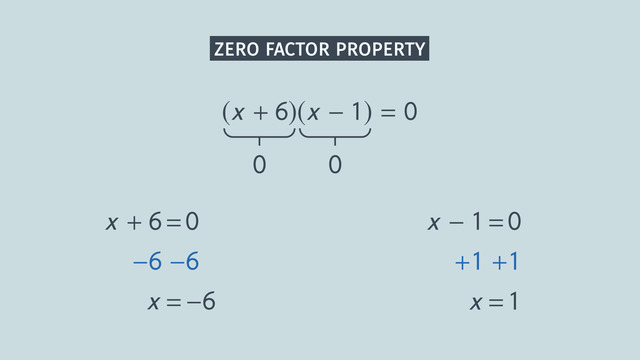

Basics on the topic Solving Quadratic Equations by Factoring
By this time, you may already be familiar with the zero property of multiplication. You may also recall that the FOIL method is a handy tool when multiplying two binomials. These two techniques come in handy when using the factoring method for solving quadratic equations.
The zero property of multiplication tells us that if at least one of the factors is equal to zero, then the product is equal to zero.
The FOIL method tells us that (x + m)(x + n) = x2 + nx + mx + mn = x2 + (n + m)x + nm.
So, if we are given the quadratic equation: x2 + bx + c = 0, we just need to do the following: Using the reverse FOIL method, find the factors of c (m and n) that will make both of the following statements true: m * n = c and m + n = b. Express the equation in the form (x + m)(x + n) = 0. Because of the zero property, we can equate x + m = 0 and x + n = 0. Replace x with either values of the roots in the original equation to check.
When you watch this video, you will see a clearer picture of solving quadratic equations by factoring with concrete examples.
Analyze Functions Using Different Representations.
CCSS.MATH.CONTENT.HSF.IF.C.8.A
Transcript Solving Quadratic Equations by Factoring
Every day in San Francisco, on Pier 39, there is a street performer named FOIL. People pass by him, but no one seems to notice the inconspicuous man. FOIL has a secret. At night, he morphs into a superhero, armed with a sparkling wit and powerful tools: factors, sums, the Zero Factor Property and most importantly, his powerful calculator wrist. What’s that, you ask? Hold on to that thought. The mayor has just made an announcement: his two daughters have been kidnapped by a pair of bad guys and they are holding the girls by the dock but can he save the girls and foil the crime just in time?
FOIL will need his calculator, his super smarts and how to solve quadratic equations by factoring. The girls are locked up in a container secured by a very complicated code. It won’t be easy to crack this code. To figure it out, FOIL must find the solutions for this quadratic equation.
Zero Factor Property
Let’s start by having a look at the Zero Factor Property. In this example, either one or both of the factors have to be zero to get a true statement. It's important that you always set the expression equal to zero, otherwise this rule won’t work. Set each set of parentheses equal to zero. If you use opposite operations, you should get two answers for x, -6 and 1. When you plug either of these two values into the original equation, you should get 0. Remember to always check your solutions.
Reverse FOIL Method
Now that we understand the main concept of the Zero Factor Property, let’s look at the quadratic equation FOIL has to solve. To factor this quadratic equation we can use the reverse foil method. We have to find the values for the variables 'm' and 'n'. In our example, m(n) = -6 and mx + nx = 1x. Therefore, 'm' plus 'n' have to be equal to 1. So now we have to find factors of -6 that sum to 1. As you can see, the product of -2 and 3 is equal to -6 and the sum of -2 and 3 is equal to 1. Perfect, we found the values for 'm' and 'n', so we can subtitute the variable 'm' and 'n' in the reverse FOIL method with these values.
So we factored our quadratic equation into two binomials (x-2) and (x+3). As always, it’s a good idea to check your work by FOILing. Good job, the factorization is proved. But, FOIL's work is not done. Although he's figured out the factors, he doesn't have a solution. To calculate the solution and free the girls, he must use the Zero Factor Property. He sets each binomial factor to zero and solves for 'x' in each case. By using opposite operations, he gets two answers for 'x', -3 and 2.
Let’s try some more problems and investigate some strategies to make these calculations easier to work with. For this first problem, modify the equation to write it in standard form to set the equation equal to zero. Now use the reverse of FOIL to factor, and then apply the Zero Factor Property to find the solutions for the variable. For this equation there is just one solution, x equals 2. I know you're anxious to find out what’s happening on the dock, but be patient.
Let’s work out one last example. This problem looks different because it has no constant. To solve, you can factor out the greatest common factor, which is 'x'. The first solution for 'x' is zero, and the second solution is 8. Don't forget to check your answer by substituting the values for 'x' into the original equation to make sure you get a true statment because even super heros can make mistakes!
Now, back to the kidnapping. FOIL enters the code and saves the girls. Now his big moment has come. Time to get famous. But no one is exactly sure what he looks like maybe he should think about a new material for his costume.
Solving Quadratic Equations by Factoring exercise
-
State the solutions of the equation $(x+6)(x-1)=0$.
HintsSure $4\times 0=0$ as well as $0\times 5=0$.
Here you see an example for the solution of an equation.
You can check your solutions by putting them into the starting equation.
SolutionThe zero factor property says that if a product $a\times b$ is equal to zero, then one of its factors, either $a$ or $b$, is equal to zero.
We can use this fact to solve factorized quadratic equations. For example,
$(x+6)(x-1)=0$.
By the zero factor property, we know that either $x+6=0$ or $x-1=0$. Using opposite operations we get
$\begin{array}{rcl} x+6 & = & ~0\\ \color{#669900}{-6} & &\color{#669900}{-6}\\ x & = & ~-6 \end{array}$
as well as
$\begin{array}{rcl} x-1 & = & ~0\\ \color{#669900}{+1} & &\color{#669900}{+1}\\ x & = & ~1 \end{array}$
So, we can conclude that the equation above has two solutions: $x=-6$ or $x=1$.
-
Solve the quadratic equation.
HintsTo factor a quadratic term $ax^2+bx+c$, find the factors of $a\times c$ which sum to $b$.
Use the zero factors property: if a product is zero, then one of its factors must be zero.
To solve linear equations use opposite operations.
SolutionIf we could factor the quadratic term $x^2+x-6=(x+m)(x+n)$, then we would be able to solve this equation using the zero factor property.
With the reverse FOIL method we can determine $m$ and $n$ as follows:
- $(x+m)(x+n)=x^2+nx+mx+mn=x^2+(m+n)x+mn$.
- So we have to find the $m$ and $n$ which statisfy $m\times n=-6$ and $m+n=1$.
- Let's check:
- $-1\times 6=-6$ but $-1+6=5$
- $1\times (-6)=-6$ but $1-6=-5$
- $-2\times 3=-6$ and $-2+3=1$ $~~~~~$✓
$(x-2)(x+3)=0$.
Thus we have to solve $x+6=0$ and $x-1=0$. Using opposite operations we get
$\begin{array}{rcl} x-2 & = & ~0\\ \color{#669900}{+2} & &\color{#669900}{+2}\\ x & = & ~2 \end{array}$
as well as
$\begin{array}{rcl} x+3 & = & ~0\\ \color{#669900}{-3} & &\color{#669900}{-3}\\ x & = & ~-3 \end{array}$
Thus the solutions are $x=2$ or $x=-3$.
-
Determine the solutions of the factorized equations.
HintsUse the zero factors property: if a product is zero, then one of its factors must be zero.
Each factor is linear. To solve a linear equation use opposite operations.
You can solve an equation like $x^2-8x=0$ as follows:
- Factor out an $x$ to get $x(x-8)=0$.
- Thus either $x=0$ or $x-8=0$, which is equivalent to $x=8$.
Solution$(x-1)(x-2)=0$: either $x-1=0$ or $x-2=0$. This leads to the following solutions
$\begin{array}{rcl} x-1 & = & ~0\\ \color{#669900}{+1} & &\color{#669900}{+1}\\ x & = & ~1 \end{array}$
or
$\begin{array}{rcl} x-2 & = & ~0\\ \color{#669900}{+2} & &\color{#669900}{+2}\\ x & = & ~2 \end{array}$
$~$
$(2x+4)(x-5)=0$: either $2x+4=0$ or $x-5=0$. So we solve these equations to get
$\begin{array}{rcl} 2x+4 & = & ~0\\ \color{#669900}{-4} & &\color{#669900}{-4}\\ 2x & = & ~-4 \\ \color{#669900}{\div 2} & &\color{#669900}{\div 2}\\ x&=&~-2 \end{array}$
or
$\begin{array}{rcl} x-5 & = & ~0\\ \color{#669900}{+5} & &\color{#669900}{+5}\\ x & = & ~5 \end{array}$
$~$
$(x+7)(-x+3)=0$: either $x+7=0$ or $-x+3=0$. Again we use opposite operations to solve those equations
$\begin{array}{rcl} x+7 & = & ~0\\ \color{#669900}{-7} & &\color{#669900}{-7}\\ x & = & ~-7 \end{array}$
or
$\begin{array}{rcl} -x+3 & = & ~0\\ \color{#669900}{+x} & &\color{#669900}{+x}\\ 3 & = & ~x \end{array}$
$~$
Let's have a look at a last example $x^2+4x=0$ which isn't factored yet. You can factor out $x$ to get $x(x+4)=0$. So either $x=0$ or $x+4=0$. We still have to solve the second equation:
$\begin{array}{rcl} x+4 & = & ~0\\ \color{#669900}{-4} & &\color{#669900}{-4}\\ x & = & ~-4 \end{array}$
-
Multiply the two binomials using the FOIL method.
HintsFOIL is a mnemonic device for multiplying binomials:
- First
- Outer
- Inner
- Last
Here you see an example using FOIL:
$(x-5)(x+2)=$
- F: $x\times x=x^2$
- O: $x\times 2=2x$
- I: $-5\times x=-5x$
- L: $-5\times 2=-10$
Add and combine the like terms. For the example above we get
$x^2+2x-5x-10=x^2-3x-10$.
SolutionFOIL is a mnemonic device for multiplying two binomials:
First, Outer, Inner, Last.
$~$
$(2x-1)(x+1)=$
- F: $2x\times x=2x^2$
- O: $2x\times 1=2x$
- I: $-1\times x=-x$
- L: $-1\times 1=-1$
$(x-5)(2x+2)=$
- F: $x\times 2x=2x^2$
- O: $x\times 2=2x$
- I: $-5\times 2x=-10x$
- L: $-5\times 2=-10$
$(x+3)(x-3)=$
- F: $x\times x=x^2$
- O: $x\times (-3)=-3x$
- I: $3\times x=3x$
- L: $3\times (-3)=-9$
$(x-3)(x-3)=$
- F: $x\times x=x^2$
- O: $x\times (-3)=-3x$
- I: $-3\times x=-3x$
- L: $(-3)\times (-3)=9$
-
Check the factorization.
HintsFOIL is a mnemonic device for multiplying binomials:
- First
- Outer
- Inner
- Last
Here you see an example for using FOIL.
$2x$ and $x$ are like terms and can be combined to get $2x+x=3x$.
Two terms are correct.
SolutionFOIL is a mnemonic device for multiplying binomials. The letters stand for
- First
- Outer
- Inner
- Last
- F: $x\times x=x^2$
- O: $x\times 3=3x$
- I: $-2\times x=-2x$
- L: $-2\times 3=-6$
$x^2+3x-2x-6$
and combing the like terms gives
$x^2+x-6$.
So we have together
$x^2+x-6=(x-2)(x+3)$.
-
Determine the code.
HintsTo factor a quadratic term $x^2+bx+c$, find the factors of $c$ which sum to $b$.
For the equation above, check all factors of $m\times n=-28$ and pick the pair $m$ and $n$ satisfying $m+n=-3$.
If you know the factorization, for example $(x-2)(x+15)$, just solve the two equations:
- $x-2=0$
- $x+15=0$
Check your solution: put both solutions for $x$ into the equation above to see if they satisfy it.
SolutionTo solve this quadratic equation we factorize the quadratic term $x^2-3x-28$.
For this we check the factors $m\times n=-28$ and choose those which sum to $m+n=-3$:
- $m=-1$ and $n=28$ but $m+n=27$
- $m=1$ and $n=-28$ but $m+n=-27$
- $m=-2$ and $n=14$ but $m+n=12$
- $m=2$ and $n=-14$ but $m+n=-12$
- $m=-4$ and $n=7$ but $m+n=3$
- $m=4$ and $n=-7$ and $m+n=-3$ $~~~~~$✓
$(x+4)(x-7)=0$.
We conclude that either $x+4=0$ or $x-7=0$. Using opposite operations we get
$\begin{array}{rcl} x+4 & = & ~0\\ \color{#669900}{-4} & &\color{#669900}{-4}\\ x & = & ~-4 \end{array}$
as well as
$\begin{array}{rcl} x-7 & = & ~0\\ \color{#669900}{+7} & &\color{#669900}{+7}\\ x & = & ~7 \end{array}$
Now we know Grandma Millers Code: $x=-4$ and $x=7$.
What are Quadratic Functions?
Graphing Quadratic Functions
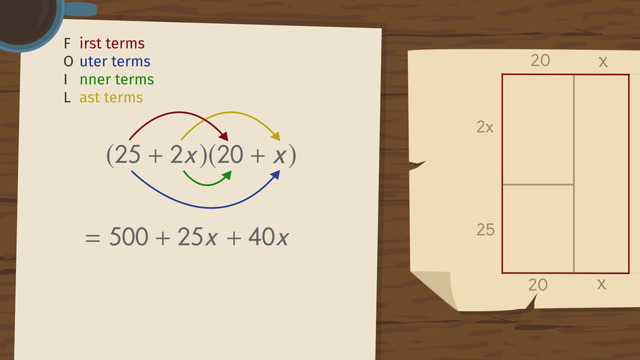
FOILing and Explanation for FOIL

Solving Quadratic Equations by Taking Square Roots
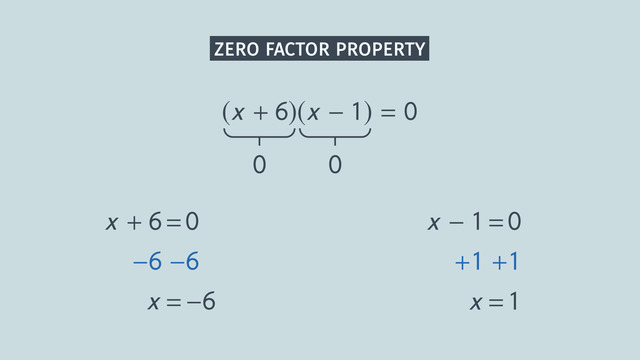
Solving Quadratic Equations by Factoring
Factoring with Grouping

Solving Quadratic Equations Using the Quadratic Formula

Solving Quadratic Equations by Completing the Square
Finding the Value that Completes the Square
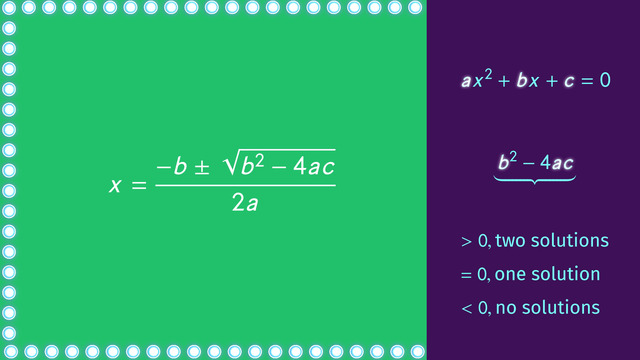
Using and Understanding the Discriminant
Word Problems with Quadratic Equations











