Graphing Quadratic Functions

Basics on the topic Graphing Quadratic Functions
The graph of a quadratic function f(x) = ax2 + bx + c is a parabola, a symmetrical U-shaped curve which opens upwards when a is positive or downwards when a is negative.
To graph a parabola, first determine the maxima, or minima, of the parabola: the vertex (x,y) such that x = -b/2a and y = f(-b/2a). Plot this point in a (x,y)-coordinate system.
The axis of symmetry is the imaginary vertical line x = -b/2a that cuts the parabola in half. Plot two more points found on the right and left sides of the axis of symmetry which satisfy the given quadratic function.
Finally, connect these points with the vertex by drawing a smooth curve. The graph produced is a parabola.
Graph linear and quadratic functions and show intercepts, maxima and minima.
CCSS.MATH.CONTENT.HSF.IF.C.7.A
Transcript Graphing Quadratic Functions
Twins, Noah & Joah, have a zoo that travels around the MPI System showing the different animals from around the galaxy. Since they don’t want to harm the animals, the twins have designed a tractor beam that gently plucks the animals and sends them to the animal sanctuary on their mothership, “The ARC”.
Coefficients of Quadratic Functions
The twins love quadratic equations. Being twins, Noah & Joah have a natural love for the number 2 and since quadratic functions have a degree of 2, they designed their spaceship’s tractor beam by graphing quadratic functions. The twins need to diversify their collection of animals. They’ve come to planet Nileesh in search of one small and one large animal to add to their collection. Let’s take a closer look at how the tractor beam works.
Coefficient ‘a’
The quadratic function graph that the twins use to collect the animals has a negative ‘a’ value. You might remember from math class that when quadratic functions have negative ‘a’ values, the graph, a parabola, opens downwards. The closer the ‘a’ value is to 0, the wider the parabola becomes.
Continuing with the ‘a’ coefficient, when the value of ‘a’ is positive the graph of the parabola opens upwards. The behavior of the graph is the same, the further away the absolute value is from 0 the thinner the parabola becomes. Look what happens when a = 0. Since multiplying anything by 0 equals 0, we're left with f(x) = bx + c, which is just a linear function.
Coefficient ‘b’
The coefficient ‘b’ alters the position of the vertex. So, how do you find the vertex? When given a quadratic function, you can get the x-coordinate of the vertex by using the following equation: x = -b / 2a. That’s great, but if we want to graph this point, we need a y-coordinate as well. To find the y-coordinate of the vertex, we simply have to plug in our solution for the x-value into the standard form equation and now we have our y-coordinate!
Let's plug in -3 for 'b', 1 for 'a' and 0 for 'c'. The x-coordinate of the vertex is -b/2a, so -(-3)/2(1), which equals 3/2. Plugging this back into our equation, f(3/2) = x2 - 3x, we get f(x) = -9/4. Notice how the position of the vertex changes. Let's take a look at some other values of 'b'. The sign of the quadratic coefficient, 'a', and the sign of ‘b’ also help to determine the direction of the shift. The axis of symmetry moves to the right of the origin if the coefficients ‘a’ and ‘b’ have different signs. The axis of symmetry moves to the left if the coefficients ‘a’ and ‘b’ have the same sign.
Coefficient ‘c’
The coefficient ‘c’ simply raises and lowers the parabola’s vertex. The twins spot a small animal Oh wow! It’s a Weebo! The twins need an ‘a’ value to just cover it. Noah knows that the bigger the absolute value of the coefficient 'a', the thinner** the parabola and, since the Weebo is below the spaceship, the 'a' value should be negative as well. Perfect! Oh no! The Weebo is making a run for the bushes. The twins have to change the value of the 'b' coefficient so that the signs of 'a' and 'b' have different signs for the vertex to move to the right. Since the tractor beam needs to be concentrated on the animal, Noah adjusts the 'c' value to -3 to place the tractor beam right above the Weebo.
Great! One down and one to go! Noah and Joah spot a large animal they've never seen before. It's a ginormous manto! Noah sets the tractor beam value for the 'a' coefficient to a wide setting, -0.1. What a relief! It's just enough to cover the large animal. After bringing the animals back to the ship, Joah's in charge of sending them to The ARC safely. Joah reverses the tractor beam by setting the 'a' value to a positive number. The Weebo goes to the mothership with no problems! People will be excited to see these exotic creatures! Joah is set to raise the Manto to The ARC. He sets the 'a' coefficient value to 0.1 and, and maybe the twins have bitten off more than they can chew...
Graphing Quadratic Functions exercise
-
Describe how the coefficients change the graph.
HintsLet $b=c=0$ and let $a$ vary to see what happens. For example:
$f(x)=x^2$ or $f(x)=3x^2$ ...
Keep in mind:
- $a$ controls the width of the parabola and if it opens downwards or upwards.
- $b$ causes a shift along the $x$-axis.
- $c$ causes a shift along the $y$-axis.
The vertex is the lowest or the highest point of a parabola, depending on if the parabola is opened downwards or upwards.
SolutionLet's consider the parabolas in the picture to the right:
The impact of the coefficient $a$
Let's start with the green parabola, which belongs to $f(x)=x^2$; so $a=1$ and $b=c=0$. This parabola is upwards opened as $a>0$. If $a<0$ the parabola is downwards opened: for example, the blue one belonging to $f(x)=-x^2$.
The coefficient $a$ impacts the graph in another way: the greater the absolute value of $a$ the thinner the parabola. Let's have a look at the yellow one, $f(x)=-\frac12x^2$. This parabola is wider than the blue one, or in other words, the blue one is thinner than the yellow one.
The impact of the coefficient $b$
The coefficient $b$ causes a shift of the vertex. Let's have a look at the violet parabola belonging to $f(x)=-x^2-4x-3$. Because $a=-1$ and $b=-4$ have the same sign, the vertex is shifted to the left. For $a=1$ we can conclude: for $b>0$ ($b<0$) the vertex is shifted to the left (right).
The impact of the coefficient $c$
The red parabola belongs to $f(x)=x^2+2$ and it is shifted upwards. So for all $c>0$ the parabola is shifted upwards and for $c<0$ downwards.
-
Explain the change of the axis of symmetry depending on $a$ and $b$.
HintsThe lowest or the highest point of a parabola is called the vertex.
The line parallel to the $y$-axis, passing through the vertex, is the axis of symmetry of the parabola.
The $x$-coordinate of the vertex is given by $x=-\frac b{2a}$.
Determine the sign of this $x$-coordinate depending on the signs of $a$ as well as of $b$.
SolutionThe lowest, for upwards opened parabolas, or the highest, for downwards opened parabolas, point is called the vertex. The line parallel to the $y$-axis, passing this vertex is the axis of symmetry of the corresponding parabola.
The $x$-coordinate of the vertex is given by $x=-\frac b{2a}$.
Thus we can conclude that for $b=0$ the vertex lies on the $y$-axis and thus this axis is also the axis of symmetry.
Let us consider the following cases:
- $a>0$ and $b>0$. This gives us $x<0$, a negative $x$-coordinate of the vertex $\rightarrow$ the axis of symmetry is shifted to the left.
- $a>0$ and $b<0$ leads to a positive $x$-coordinate and thus to a right-shift.
- $a<0$ and $b>0$ leads to a positive $x$-coordinate as well and also to a right-shift.
- $a<0$ and $b<0$ gives us a negative $x$-coordinate, that means a shift to the left of the axis of symmetry.
-
Determine the corresponding function.
HintsIf the vertex is lying on the $y$-axis, we have $b=0$.
If $a>0$ ($a<0$) the parabola is opened upwards (downwards).
Changing $c$ causes a shift upwards or downwards depending on the sign of $c$.
You can also check the vertex each time.
SolutionHow can we determine the corresponding function for each parabola?
First look at how it opens: is it opened upwards or downwards? If the parabola is opened upwards we have $a>0$ and $a<0$ otherwise. So the green, red, and orange parabolas have a positive $a$ and the blue one has a negative $a$.
Next we look at the vertex:
- If the $x$-coordinate is zero, we can conclude that $b=0$. So the blue, the green, and the red parabolas have $b=0$, while for the orange one $b\neq 0$.
- If the vertex is $(0,0)$ the corresponding equation is given by $f(x)=ax^2$, otherwise it is given by $ax^2+c$, where $c$ is the $y$-intercept.
- Let's start with the blue one: $a<0$ and $b=c=0$. Because $(1,-1)$ is one point on the parabola, we can conclude the corresponding function is $f(x)-x^2$.
- The green one has $a>0$ and $b=c=0$. Let's check one point $(1,2)$, so $x=1$ and $y=2$. This is fulfilled for $f(x)=2x^2$.
- The yellow one is the only parabola with a vertex not lying on the $y$-axis. Thus $b\neq 0$. Let us check the point $(1,0)$: $f(1)=1^2-1=0$, as desired. So $f(x)=x^2-x$ is the corresponding function.
- Last but not least, the red one with the vertex $(0,3)$; so $a>1$, $b=0$m and $c=3$. The only function fulfilling this is $f(x)=x^2+3$.
-
Decide which function belongs to which graph.
HintsNote that you don't have to pay attention to the width of the parabola.
For $a>0$ ($a<0$) the parabola is opened upwards (downwards).
Pay attention to the vertex: if the vertex lies on the $y$-axis, you have that $b=0$.
You can also check points lying on the parabola: if you put the $x$-coordinate in the function you get the $y$-coordinate.
SolutionLet's start with the grey and blue parabolas, which have a vertex on the $y$-axis; the corresponding equation is $f(x)=ax^2+c$.
For each of these parabolas, $a$ is either $1$ and opened upwards, or $-1$ and opened downwards.
The regarding $c$ is the $y$-intercept. So, for the grey parabola we have $f(x)=-x^2+1$ and for the blue we have $f(x)=x^2+2$.
Next we investigate the green and violet parabolas, with the vertex lying on the $x$-axis. Both parabolas have $a=1$. Because the $x$-coordinate of the vertex is $-2$ for the green parabola and $2$ for the violet one, we can determine $b$ as follows:
- For the green one, $-2=-\frac{b}{2a}$. Keeping in mind that $a=1$, we get $b=4$. $c$ is the $y$-intercept, namely $4$. Thus we get the resulting function $f(x)=x^2+4x+4$.
- For the violet one, $2=-\frac{b}{2a}$. Keeping in mind that $a=1$, we get $b=-4$. $c$ is the $y$-intercept, namely $4$. Thus we get the resulting function $f(x)=x^2-4x+4$.
- The red one has the vertex $(-4,2)$ and is upwards opened. Using this vertex we can conclude $f(x)=(x+4)^2+2=x^2+8x+16+2=x^2+8x+18$.
- The yellow one has the vertex $(3,3)$ and is downwards opened. Using this vertex we can conclude $f(x)=-(x-3)^2+3=-x^2+6x-9+3=-x^2+6x-9$.
$f(2)=-2^2+6(2)-6=-4+12-6=2$ $~~~~~$✓
-
Check the following statements.
HintsHere you see a parabola where the vertex has a positive $x$-coordinate and a negative $y$-coordinate. The green line is the axis of symmetry.
Here you see a few parabolas.
This is a linear function, which has a line as a graph.
SolutionA quadratic function in standard form is given by
$f(x)=ax^2+bx+c$.
Let $a=1$ and $b=c=0$.
We then get $f(x)=x^2$, a special quadratic function.
The graph of a quadratic function is a parabola. Beside you see a picture of different parabolas.
A parabola can be upwards, or downwards, opened depending on the sign of $a$:
- upwards for $a>0$
- downwards for $a<0$
Each parabola has a line parallel to the $y$-axis, passing the vertex, which is its axis of symmetry.
-
Describe how to determine the vertex.
HintsDetermine the $x$-coordinate, $x=-\frac b{2a}$, first.
If you know the $x$-coordinate, you get the $y$-coordinate by pugging the $x$-coordinate into the function.
Let's have a look at an example: $f(x)=2x^2-2x+1$. Here we have $b=-2$.
- $x=-\frac{-2}{2(2)}=\frac12$
- $y=2\left(\frac12\right)^2-2\left(\frac12\right)+1=\frac12-1+1=\frac12$.
$\left(\frac12,\frac12\right)$
SolutionThe quadratic function we are considering is $f(x)=2x^2+bx+1$.
What is the impact of changing values for $b$ on the vertex?
The vertex is the highest or lowest point of the parabola.
The $x$-coordinate is given as $x=-\frac{b}{2a}=-\frac b4$.
We start with $b=2$:
- $x=-\frac24=-\frac12$.
- Now we put this $x$ in $f(x)=2x^2+2x+1$ and get $y=2\left(-\frac12\right)^2+2\left(-\frac12\right)+1=\frac12-1+1=\frac12$.
In a similar manner we can determine the vertex for $b=4$:
- $x=-\frac44=-1$.
- Now we put this $x$ into the function $f(x)=2x^2+4x+1$ and get $y=2\left(-1\right)^2+4\left(-1\right)+1=2-4+1=-1$.
Lastly we figure out the vertex for $b=-4$:
- $x=-\frac{-4}4=1$.
- Now we put this $x$ in the functional equation $f(x)=2x^2-4x+1$ and get $y=2\left(1\right)^2-4\left(1\right)+1=2-4+1=-1$.
Now the twins have all the information they need to catch the animals they want for their zoo.
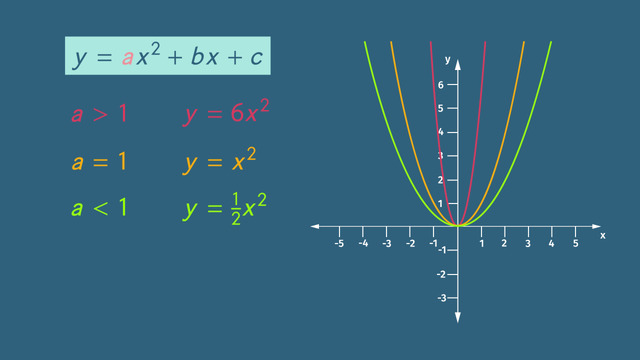
What are Quadratic Functions?

Graphing Quadratic Functions
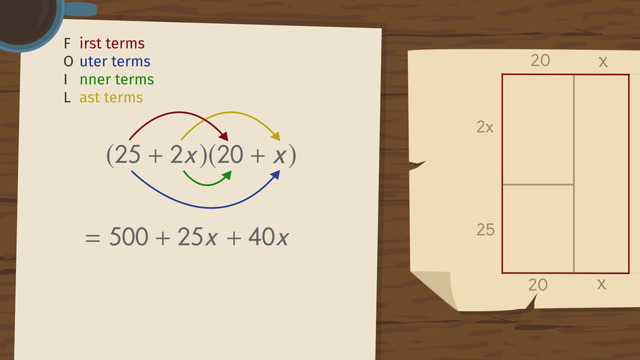
FOILing and Explanation for FOIL

Solving Quadratic Equations by Taking Square Roots
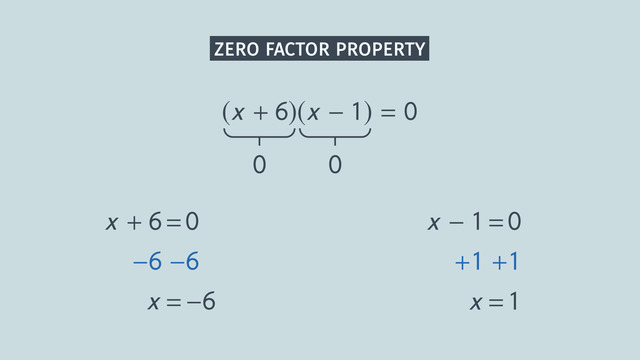
Solving Quadratic Equations by Factoring
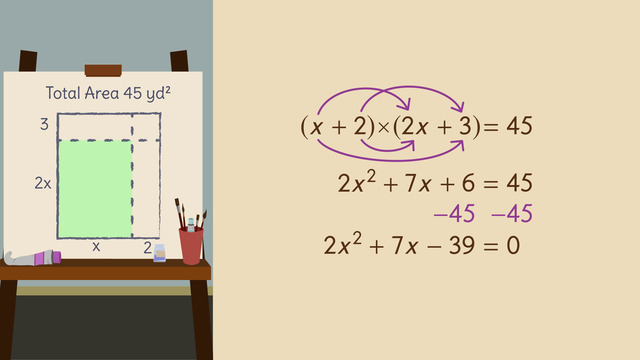
Factoring with Grouping

Solving Quadratic Equations Using the Quadratic Formula

Solving Quadratic Equations by Completing the Square
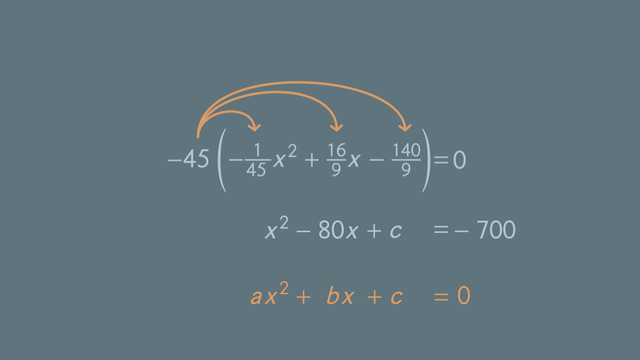
Finding the Value that Completes the Square
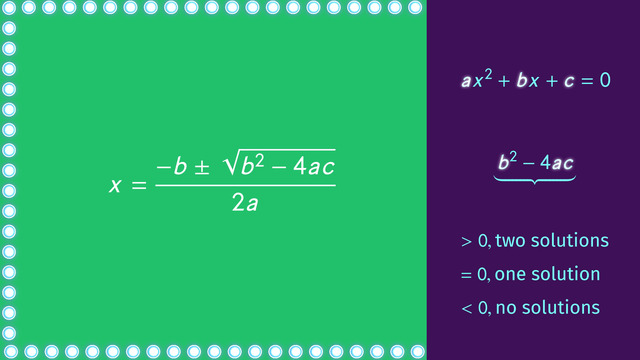
Using and Understanding the Discriminant
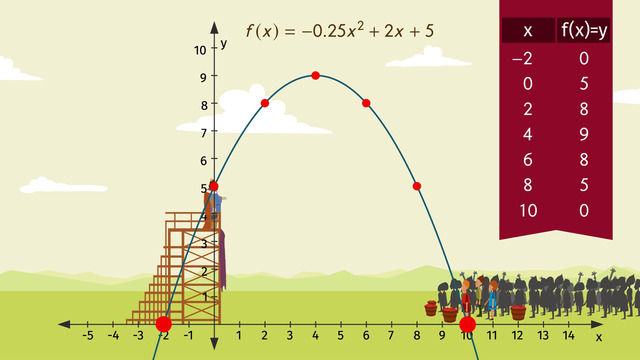
Word Problems with Quadratic Equations











