Using Nets to Find Surface Area
- Using Nets to Find Surface Area
- Using Nets to Find Surface Area – Explanation
- Using Nets to Find Surface Area – Step-by-Step Process
- Surface Area of a Right Rectangular Prism
- Surface Area of a Right Rectangular Pyramid
- Surface Area of a Triangular Prism

Basics on the topic Using Nets to Find Surface Area
Using Nets to Find Surface Area
Using nets to calculate the surface area of three-dimensional shapes is a practical and visual method. A net represents a three-dimensional object as a two-dimensional layout that can be folded to reconstruct the object. This method is utilized in various real-world applications, such as packaging design and material estimation.
Surface Area is the combined area of all faces and curved surfaces of a three-dimensional object.
Nets are the unfolded two-dimensional representations of these objects, aiding in the straightforward computation of their surface areas.
Using Nets to Find Surface Area – Explanation
The process of calculating the surface area using nets involves unfolding a three-dimensional figure (like a prism or pyramid) into a flat arrangement of its faces. For this topic, we focus on nets for three shapes: right rectangular prisms, right rectangular pyramids, and right triangular prisms.
| 3D Shape Name | 3D Shape (Illustration of the 3D version) | 2D Shapes Formed (Describe the Net) | 2D Net (Illustration Request) |
|---|---|---|---|
| Right Rectangular Prism | Illustration request: A 3D right rectangular prism. | The net consists of three pairs of rectangles, corresponding to the opposite faces of the prism. | Illustration request: A net of a right rectangular prism |
| Right Rectangular Pyramid | Illustration request: A 3D right rectangular pyramid(no labels needed) | The net includes one square base and four triangular faces that connect at the apex of the pyramid. | Illustration request: A net of a right rectangular pyramid |
| Right Triangular Prism | Illustration request: A 3D right triangular prism. | The net features two right triangles for the bases and three rectangles corresponding to the sides of the prism. | Illustration request: A net of a right triangular prism - no labels needed. |
Using Nets to Find Surface Area – Step-by-Step Process
In this section, we explore how to determine the surface areas of various three-dimensional shapes using their corresponding two-dimensional nets. Mastering these calculations involves foundational concepts such as finding the area of a right triangle, understanding the area of a shape, and calculating the area of rectangles. By breaking down complex shapes into simpler 2D nets, we can apply these basic area formulas to find the total surface area effectively.
Surface Area of a Right Rectangular Prism
Steps to Find the Surface Area:
Identify the Dimensions: The dimensions are 6 cm (length), 4 cm (width), and 3 cm (height).
-
Calculate Area of Each Face:
- Two rectangles of $6 \times 4$ cm: $2 \times (6 \times 4) = 48$ cm²
- Two rectangles of $6 \times 3$ cm: $2 \times (6 \times 3) = 36$ cm²
- Two rectangles of $4 \times 3$ cm: $2 \times (4 \times 3) = 24$ cm²
Add All Areas Together: Total surface area = $48 + 36 + 24 = 108$ cm²
Surface Area of a Right Rectangular Pyramid
Steps to Find the Surface Area:
Identify the Dimensions: This triangular pyramid has a base of 4 cm per side and a slant height of 5 cm for the triangular sides.
-
Calculate Area of the Base:
- Base area (square) = $4 \times 4 = 16$ cm²
-
Calculate Area of Triangular Sides:
- Triangular side area = $\frac{1}{2} \times 4 \times 5 = 10$ cm²
- There are four triangular sides: $4 \times 10 = 40$ cm²
Add Base and Side Areas: Total surface area = $16 + 40 = 56$ cm²
Surface Area of a Triangular Prism
Steps to Find the Surface Area:
Identify the Dimensions: For the net of the prism, we have one rectangular base with the dimensions of 7 cm by 10 cm, and two rectangles with dimensions of 6 cm by 10 cm.
Calculate Area of the Triangular Bases:
The triangular base area = $\frac{1}{2} \times 7 \text{ cm} \times 5 \text{ cm} = 17.5 \text{ cm}^2$
Two bases: $2 \times 17.5 \text{ cm}^2 = 35 \text{ cm}^2$
Calculate Area of Rectangular Sides:
Base rectangle: $7 \text{ cm} \times 10 \text{ cm} = 70 \text{ cm}^2$
Side rectangles: $6 \text{ cm} \times 10 \text{ cm} = 60 \text{ cm}^2$ for each, $2 \times 60 \text{ cm}^2 = 120 \text{ cm}^2$ for both
Add All Areas Together: Total surface area = $35 \text{ cm}^2 + 70 \text{ cm}^2 + 120 \text{ cm}^2 = 225 \text{ cm}^2$
Therefore, the surface area of the triangular prism is 225 cm².
Using Nets to Find Surface Area – Practice
Using Nets to Find Surface Area – Summary
Key Learnings from this Text:
Nets simplify the calculation of surface area by presenting 3D objects as connected 2D shapes.
Skills in using nets are applicable in real-world scenarios such as packaging design and material estimation.
The process includes unfolding a 3D shape into a net, calculating the area of each face, and summing these areas to find the total surface area.
Using Nets to Find Surface Area – Frequently Asked Questions
Transcript Using Nets to Find Surface Area
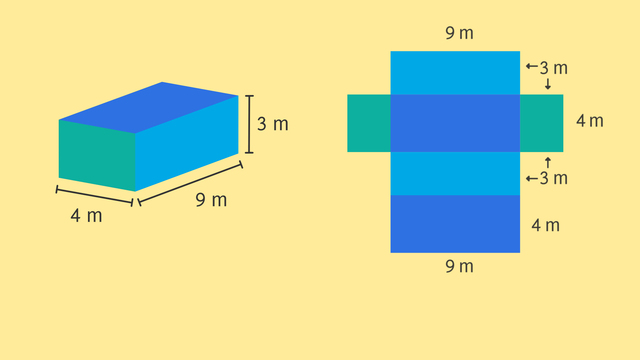
After months of persistence, Dwayne has earned the prestigious title of Assistant Regional Resident Assistant! He's quite proud of his title and that means his arch-nemesis Steve HAS to play a prank on him. Let's see what Steve's got up his sleeve! Steve's gonna cover Dwayne's room with sticky notes! How many notes will it take? We can use nets to find the surface area of the room to find out! The room is a rectangular prism that is 4 meters wide 3 meters tall and 9 meters long. We can unfold this rectangular prism to get a net, or 2 dimensional flattening of the prism. A net is useful because, with a net, we can easily see each face, or two-dimensional side, of the prism. There are 6 faces. Because opposite faces of the prism are the same there are 3 pairs of identical faces here, here and here. The aurface area of the prism is the SUM of the areas of all the faces. Each face is a rectangle. And we know that the area of each rectangle is its length times its width. So to find the surfface area of this rectangular prism, we need to find the area of each pair of rectangles making up the prism, and then add all of these areas together to get the surface area of Dwayne's room. Let's start with these two. The area of each is 3 times 4, which is 12 square meters. Now let's look at these two. The area is 3 times 9, which is 27 square meters. Now, these two. 4 times 9 is 36. To calculate the surface area, we can now plug in 12 for the area of face one and the face 2, 27 for area of face three and face 4 and 36 for the area of face five and face six. Simplifying, we get 2 times 12 plus 2 times 27 plus 2 times 36. Simplifying further, we have 24 plus 54 plus 72 for a total surface area of 150 square meters. Now that Steve knows the surface area of Dwayne's room, he can get to work on posting the post-its! Steve's gotta work fast before Dwayne returns! Where IS Dwayne anyway? Oh man, Dwayne is up to shenanigans of his own in Steve's room! What's this? A blueprint for something devious it seems. We've got a square base that's 3 meters by 3 meters and four triangular lateral faces that have a height of 4.5 meters. This looks like a net for a 3-dimensional shape but what shape is it? That's right! It's the net of a square pyramid. Let's find the surface area of this square pyramid by using its net to visualize its faces. The area of the square is 3 times 3 which is 9 square meters. The area of each triangle is half the base length, times the height. That's one-half, times 3, times 4.5. That's half of 13.5, or 6.75 square meters. The surface area of this square pyramid is the sum of the areas of its faces. There are four triangles so the total surface area is 9, plus four times 6.75. That's 9 plus 27, or 36 square meters. Now Dwayne is ready to construct his pyramid scheme. Before we see which guy gets caught net-handed, let's review how we can use nets to find surface area. We can unfold rectangular prisms and square pyramids to get a 2 dimensional version called a net. We can then use a net to find the surface area by calculating the area of each face and then adding those areas together. Oh man, they finished at the same time!
Using Nets to Find Surface Area exercise
-
Understand what a net is and how to use them to find the surface area of a 3D shape.
HintsA net is like a flattened-out outline of a 3D shape.
If you have a rectangular prism, and you unfold it so it lays flat, the net would be the shape you'd see. It's all the faces spread out in 2D. Think of it like opening up a cardboard box so it's flat on the floor - that flat shape is the net of the box.
Surface area is the total area of all the surfaces of a three-dimensional object.
Imagine a cardboard box: the surface area is the amount of space covering the outside of the box, including all its sides. If you were to unfold the box and lay it flat, the surface area would be the total area of all the cardboard pieces you see.
To help you answer the question, refer to the images seen in the problem.
SolutionThe measurement that calculates the sum of the area of each of the faces of the prism is called the surface area.
A 3D shape can be unfolded to reveal a 2D flattening or what is known as a net. Finding the area of each face can help find the surface area.
-
Identify the process to finding the surface area of a net.
HintsTo find the surface area, add the area of each face of the net.
There are 2 correct answers in the problem that would find the surface area.
SolutionTo find the surface area, add the area of each face of the net. The two answers that would work to find the surface area are:
- $12 + 12 + 27 + 27 + 36 + 36$
- $(12 \times 2) + (27 \times 2) + (36 \times 2)$
-
Identify the area of the net to find the total surface area.
HintsTo find the area of a rectangle, multiply the length by the width.
Look at the face that has a measurement of 3 m and 10 m. To find the area of this face, we will use the formula $A=lw$.
Substitute in the values for $l$ and $w$.
$A=10 \times 3$
Find the product to find the area,
$A=30\:cm^2$.
SolutionThe area of each face was found and then added together to find the total surface area.
$60 + 60 + 18 + 18 + 30 + 30 = 216\:cm^2$
-
Demonstrate your understanding of the process to find the surface area using a net.
HintsA 3D rectangular prism can be flattened out into a 2D shape, which is called a net. The net can help us find the surface area.
To find the surface area of a net, you must find the area of each face.
The formula used to find the area of each face of a rectangular prism is $A=lw$. The $l$ stands for the length, and the $w$ stands for the width.
Solution1) Find the net for the rectangular prism.
2) Substitute the $l$ and $w$ in to the formula $A=lw$ and find the area.
3) The areas for each face:
- $A=6\:cm^2$
- $A=6\:cm^2$
- $A=12\:cm^2$
- $A=12\:cm^2$
- $A=18\:cm^2$
- $A=18\:cm^2$
5) The surface area is $62\:cm^2$.
-
Find the surface area of a rectangular prism as a net.
HintsTo find the surface area, add up the area of each face of the rectangular prism.
A rectangular prism has a total of 6 faces. There are two sets of each face with identical area measurements.
Addition can be used to find the total surface area. Can you find the sum?
$15 + 15 + 15 + 15 + 9 + 9 = ?$.
SolutionThe surface area of the rectangular prism is $78\:m^2$.
To find this, each area can be added together like this:
$15 + 15 + 15 + 15 + 9 + 9 = 78$.
Don't forget to add in the units, which are $m^2$.
-
Using nets to find surface area.
HintsThe first step is to find the area of each face. It is helpful to find the net of this rectangular prism first to lay out all the faces.
When a rectangular prism is turned into a net, there are six 2D rectangles.
SolutionThe areas for the faces of the rectangular prism are:
- $15\:cm^2$
- $21\:cm^2$
- $35\:cm^2$
$15(2) + 21(2) + 35(2)$
The sum of the faces of the net is equal to the surface area.
$SA=142\:cm^2$










I love this! 3D is difficult to visualise, makes it very easy to understand