Formula for Volume of a Rectangular Prism
- Understanding the Volume of a Rectangular Prism
- Formula for Volume of a Rectangular Prism
- Finding the Volume of a Prism with $V=Bh$
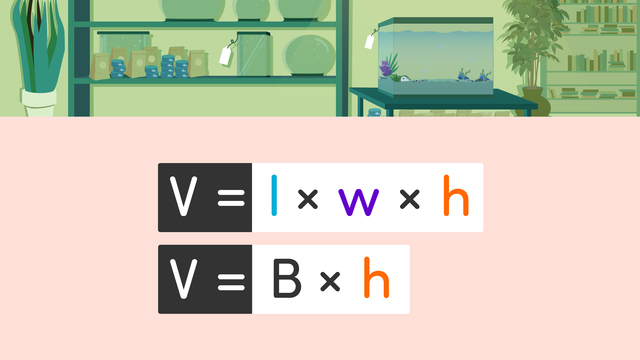

Basics on the topic Formula for Volume of a Rectangular Prism
Understanding the Volume of a Rectangular Prism
In our daily lives, we often come across objects shaped like rectangular prisms - think of boxes, bricks, or even parts of buildings. A rectangular prism is a 3D shape with six faces, each one a rectangle. When we talk about the volume of a rectangular prism using cubic units, we find out how much space it takes up. It's like figuring out how much water can fill a fish tank or how many books you can pack into a box. This volume helps us understand the capacity of these objects in cubic units, which measure space in three dimensions.
Volume Formula: The volume of a rectangular prism is calculated by multiplying its length ($l$), width ($w$), and height ($h$). The formula is $V = l \times w \times h$.
Formula for Volume of a Rectangular Prism
In math, we often have more than one way to solve a problem, and that's true for finding the volume of a rectangular prism too.
The formula $V = l \times w \times h$ directly multiplies the prism's dimensions. This method is straightforward and effective for calculating volume.
Let’s learn how to find the volume of a rectangular prism with this formula.
A rectangular prism has a length of $4$ cm, width of $3$ cm, and height of $6$ cm. Calculate its volume.
- Length ($l$) = $4$ cm
- Width ($w$) = $3$ cm
- Height ($h$) = $6$ cm
- Volume = $l \times w \times h = 4 \times 3 \times 6 = 72$ cm$^3$
The volume of this prism is $72$ cubic centimeters.
We use cubic units for units of volume because volume measures three-dimensional space. Think of stacking little blocks inside a box - you're filling it lengthwise, widthwise, and heightwise. So, we multiply these three dimensions, and the result is in cubic units, like filling a box with tiny cubes.
Find the volume of a prism with a length of 5 m, a width of 2 m, and a height of 3 m.
- Length ($l$) = $5$ m
- Width ($w$) = $2$ m
- Height ($h$) = $3$ m
- Volume = $l \times w \times h = 5 \times 2 \times 3 = 30$ m$^3$
The volume of this prism is $30$ cubic meters.
Use the formula for the volume of a rectangular prism, and solve these examples on your own!
Finding the Volume of a Prism with $V=Bh$
Another formula to find the volume of a rectangular prism is using $V = B \times h$. Here, $B$represents the area of the base of the shape. For a rectangular prism, this base is the area of the rectangle at the bottom. This formula is really helpful, not just for rectangular prisms, but also for other 3D shapes like cylinders which have a circular base (volume of a cylinder). It helps us understand how much space these shapes occupy by considering their base area and height.
Let's calculate the volume of a rectangular prism with a length of 4 feet, a width of 3 feet, and a height of 6 feet.
Determine the dimensions of the prism:
- Length ($l$) = $4$ ft
- Width ($w$) = $3$ ft
- Height ($h$) = $6$ ft
Calculate the base area (B):
- The base area is found by multiplying the length and width.
- Base Area ($B$) = $l \times w = 4 \times 3 = 12$ square feet.
Calculate the volume using $V = B \times h$:
- Now, multiply the base area by the height.
- Volume ($V$) = $B \times h = 12 \times 6 = 72$ cubic feet.
The volume of this rectangular prism is $72$ cubic feet.
Practice using this formula on your own!
Formula for Volume of a Rectangular Prism – Application
Solving problems involving the volume of a rectangular prism enhances our understanding of space and capacity. It applies in diverse fields, from architecture and construction to everyday tasks like packing or storage.
Formula for Volume of a Rectangular Prism – Summary
Key Learnings from this Text:
- Understanding the volume of a rectangular prism helps in calculating space in practical situations.
- The volume formula, $V = l \times w \times h$, is straightforward and widely applicable.
- Alternative method: $V = B \times h$, where $B$ is the base area, deepens conceptual understanding.
- Real-world application of this knowledge spans from storage organization to construction planning.
| Formula | Explanation |
|---|---|
| $V = l \times w \times h$ | Multiply length ($l$), width ($w$), and height ($h$) to find the volume. |
| $V = B \times h$ | Calculate the base area ($B$ = length x width), then multiply by height ($h$). |
Formula for Volume of a Rectangular Prism – Frequently Asked Questions
Transcript Formula for Volume of a Rectangular Prism
Formulas for Volume of a Rectangular Prism Rectangular prisms are three-dimensional shapes that have a length, width, and height. When we measure the volume, we determine how much space is INSIDE the prism and what solid, (...) liquid, (...) or gas it has the ability to hold. We know that we can divide this shape into cubic units. But what happens when the prisms grow in size? We need a more efficient way to find the volume. There are two mathematical formulas to find the cubic measurement of a rectangular prism. Remember, a formula is a mathmatical expression that helps us find a specific value. It's like a set of instructions that guide in in performing calculations. One formula for finding volume looks like this.
Formula for Volume of a Rectangular Prism exercise
-
Find the volume of the rectangular prism.
HintsTo calculate the volume, multiply the length, width, and height.
What is 10 x 5 x 5?
SolutionThe length is 10 inches, the width is 5 inches and the height is five inches.
Multiply these together: 10 x 5 x 5 = 250.
Therefore, the correct answer is $250 in^3$.
-
Label the length, width, height, and the volume.
HintsThe height is the perpendicular distance from the base to the top, the length is how long it is, and the width is perpendicular to the length.
The formula to calculate the volume is V= l x w x h.
SolutionThe length is 2in, the width is 2in, and the height is 10in.
When we multiply 10 x 2 x 2, we get the total volume of the prism, $40 in^3$.
-
Calculate the volume.
HintsThe length has 4 cubes, so the length is 4. Count the cubes to find the width and height. Then multiply.
Count the cubes to identify the length, width, and height.
SolutionThe length is 4, the width is 2, and the height is 2. Multiply 4 x 2 x 2 to get the volume, $16 in^3$.
-
Fill in the missing side to find the volume of the rectangular prism.
HintsTo find the missing side, compare the length with other side., A square has 4 equal sides.
Find the volume using the formula V= l x w x h.
SolutionThe width is 5 inches. There is a square at the end of the prism which is why the width is 5 inches. 12 x 5 x 5 = $300 in^3$.
-
Which formulas are used to find the volume of a rectangular prism?
HintsThere are two formulas used to calculate the volume of a rectangular prism.
One way to find the volume is to multiply the base times the height.
V stands for volume, b stands for base, h stands for height, and w stands for width.
SolutionTo find the volume of a rectangular prism, use V= b x h or V= l x w x h.
V stands for volume, b stands for base, h stands for height, and w stands for width.
-
Find the volume of each rectangular prism and sort from smallest to largest.
HintsUse the formula V= l x w x h to find the volume of each. Then sort from smallest to largest.
Start by calculating the volume of the purple rectangular prism. Multiply 7 x 7 x 7.
SolutionUse the formula V= l x w x h to find the volume of each. Then sort from smallest to largest.
- The volume of the red prism is $72 in^3$.
- The volume of the blue prism is $80 in^3$.
- The volume of the orange prism is $110 in^3$.
- The volume of the purple prism is $343 in^3$.
So, the shapes from smallest to largest are red, blue, orange, purple.





















