Using Trig. Ratios to Find Distances

Basics on the topic Using Trig. Ratios to Find Distances
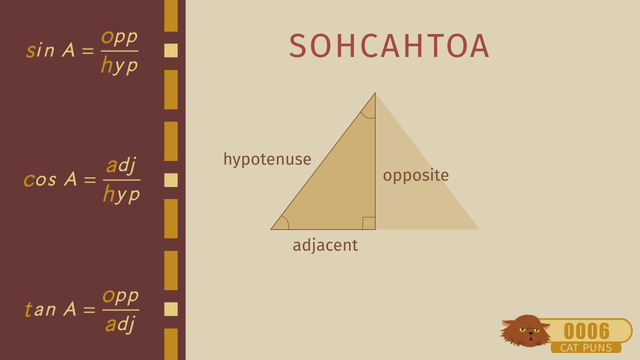
When learning about the law of sines and cosines, it is important to remember the Pythagorean Theorem: c2 = a2 + b2, and the trigonometric ratios; specifically, sine and cosine.
The law of sines and cosines is another tool for finding unknown angles and side lengths of triangles. This law was derived from the Pythagorean Theorem and trigonometric ratios and is stated as follows:
Law of Sines:
a b c ------ = ------ = ------ sinA sinB sinC
Law of Cosines:
c2 = a2 + b2 – 2ab(cosC) b2 = a2 + c2 – 2ac(cosB) a2 = b2 + c2 – 2bc(cosA)
where the lower case a,b and ,c are the lengths of the sides of the triangle and upper case A, B, and C are the measurement of the angles.
This video provides examples and shows how to use the law of sines and cosines to find angles and side lengths of a triangle.
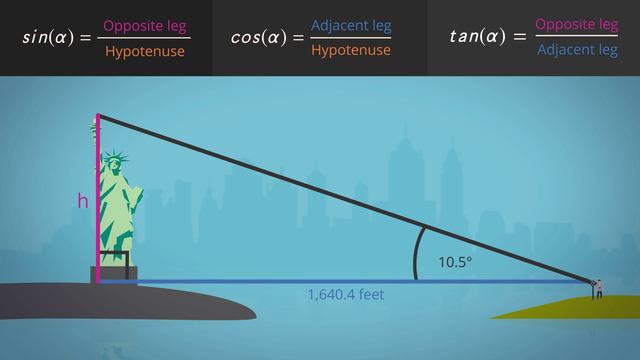
The law of sines and cosines can also be be used to find the distance of two objects. For example, if you want to find the distance between two ships in the sea from a light house, you can compute their distance once you know the length of the light beams from the lighthouse to the ships, and the angle connecting the beams.
Apply trigonometry to general triangles.
CCSS.MATH.CONTENT.HSG.SRT.D.10
Transcript Using Trig. Ratios to Find Distances
Woody is from planet MO WOOD. He, like all the other inhabitants of MO WOOD, lives in a treehouse. When the males reach the age of 26, they leave their parent’s treehouses to build a life of their own.Woody'll use the Law of Sines and the Law of Cosines to help him build the perfect tree house. Woody now has to do what all the tree people have done before him: he has to build his own tree house. Woody likes the design of his dad’s house, so he decides to take some measurements to help him get started.
Woody notices that he forms a triangle with the top and bottom of the tree house from where he stands. He recalls that he can use the Law of Cosines and the Law of Sines to find lengths as well as angle measures of non-right triangles.
Law of Cosines
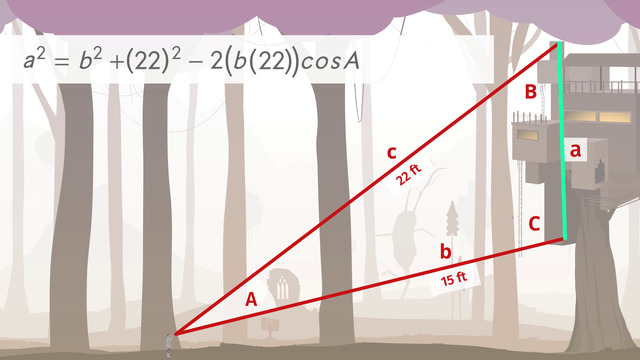
Woody knows the distances to the top and bottom of the tree house are 22 feet and 15 feet respectively. With the antique angle finder his dad gave him, Woody knows the angle is 20.38°. Does Woody have enough information in order to find the height of the living room? Let's take a closer look. The Law of Cosines is a formula you can use to find the length of an unknown side of a triangle if you know the measures of the other two sides as well as the opposite angle of the unknown side.
Let's have a look at the formula. Does the first part of the equation look familiar? It should, it's the Pythagorean Theorem! Notice how you take the cosine of the angle opposite the side you're trying to find. Finally, you multiply the cosine of this angle by 2(ab) and subtract the result from our original Pythagorean Theorem.
Since there are several ways of looking at the same triangle, there are a few variations of this equation you can use to fit your needs. See how similar the form of each equation is? To decide which formula Woody will need to figure out the height of the living room, we compare the sketch of the problem to our formulas. Depending on how you name the sides, you can use the known information to help you calculate which side you want to find. Let's assume our unknown side is 'a' and the known angle is A. Let's plug in the numbers we know so we can find the measure of the last side. First, the length of the longest side, 'c', is 22. The measurement of the second side, 'b', is 15. The angle measure formed by these two sides, ∠A, is 20.38°.
Now all we have to do is finish it off with PEMDAS! First, start with simplifying cosine within the parantheses and the exponents. Next, lets do some PEMDAS. We subtract from left to right. And finally, we get rid of the square by taking the square root of both sides of the equation. So, the height of his dad's house is approximately 9.5 feet.
Law of Sines
Now that Woody has the measurements for the height of his new home, he can focus on the exact measurements for his bedroom. This time, Woody knows two angles and one of the side lengths. One of the angles measures 50° and the other he finds is 33.23°. The side length Woody knows is 15 ft., but he's not sure of the angle opposite this side. With this information, Woody can use the Law of Sines to help him determine the other side lengths.
The Law of Sines is a simple ratio that states that the ratio of each side and its opposing angle is the same as the ratios of the other two sides and their respective opposite angles. To find the measure of the last angle, Woody subtracts the known angles from 180°, since all triangles have an internal angle measure of 180°. Now Woody knows that his final angle measure is 96.77°.mGreat! Now he can use the Law of Sines to help him figure out how tall his bedroom should be!
Since it doesn't matter which side is labeled 'a', 'b' or 'c', Woody just has to make sure that the ratios he sets up are the side lengths to opposite angles.Since all the ratios are equal and now that Woody has one complete ratio, he can calculate the lengths of the two unknown sides. Woody can isolate the variable in both of the equations and then calculates the side lengths. Let's focus on 'b' for a moment. To isolate 'b', we multiply both sides by the sine of 50. Calculating from left to right we get: ‘b' equals approximately 11.57 feet. We follow the same steps for finding the lengths for side 'c'. Since this is the leg that Woody wanted to find, he now knows how tall his bedroom should be: approximately 8.28 feet.
Awesome! Now all Woody needs to do is to pick out the perfect tree after some searching, Woody finds the perfect tree...but that’s not a tree! Run, Woody, RUN!!!
Using Trig. Ratios to Find Distances exercise
-
Explain the law of cosines.
HintsThe first part of the law of cosines is the Pythagorean theorem.
In the law of cosines, three sides and one angle are needed.
The green sides as well as the green angle are known, while the orange side is unknown.
SolutionThe law of cosines is a formula which can be used to find the unknown length of a side of a triangle, if you know the length of both other sides as well as the opposite angle of the unknown side.
You can see the corresponding formulas in the picture to the right.
How can you derive these formulas?
The first part, $c^2=a^2+b^2$ (highlighted in green in the first equation in the picture), is the Pythagorean theorem. Then you still have to subtract a product: two times the product of the length of those sides on the right side of the equation and the cosine of the opposite angle.
Let's try it with $a^2$ on the left-hand side:
- We start with $a^2=b^2+c^2$, the Pythagorean property.
- Next we subtract the double of the product of $b$ and $c$ as well as the cosine of the opposite angle of $a$, namely $A$, to get $a^2=b^2+c^2-2(bc)\cos(A)$.
-
Determine the height of the tree house.
HintsThe law of cosines is given by, for example,
$c^2=a^2+b^2-2ab\cos(C)$,
where $C$ is the angle opposite to the side $c$.
The wanted side squared is isolated on the left side of the equation. On the right side you only find known values.
Remember PEMDAS, the order of calculation:
- Paranthesis
- Exponent
- Multiplication and Division
- Addition and Subtraction.
SolutionBecause we know the lengths of two sides and we know the opposite angle of the side we would like to fine the length of, we can use the law of cosines.
Let $a$ be the unknown height:
$\begin{array}{rclll} a^2&=&~(15)^2+(22)^2\\ & &~-2((15)(22))(\cos(20.38°)) \end{array}$
Using PEMDAS we can simplify as follows
$\begin{array}{rclll} a^2&=&~225+484-660(0.9374)\\ &=&~90.31 \end{array}$
Lastly, we take the square root to get
$a\approx 9.5$.
Thus the height of the wooden house is approximately $9.5$ ft.
-
Calculate the height of the tree house.
Hints$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}$
is the law of sines.
$a^2=b^2+c^2-2bc\cos A$
is the law of cosines.
For the law of sines two sides and two angles are needed, while for the law of cosines three sides and one angle are needed.
The law of sines states that the ratio of any side and the sine of the opposite angle is the same as the ratio of any of the other sides and the sine of its opposite angle.
SolutionHow can we decide, which law we have to use?
Just look at the given information: here we know two angles (and thus three angles) and only one side. For the law of cosines we need at least two sides. So we use the law of sines.
First we determine the last angle using the facts that the three corners sum to $180$°:
$180°-64°-39°=77°$.
To get the desired side $h$, we do as follows using the law of sines:
$\frac{h}{\sin(39°)}=\frac{5.3}{\sin(77°)}$.
Almost done, we still have to multiply by $\sin(39°)$ to get
$h=\frac{5.3}{\sin(77°)}\times \sin(39°)\approx 3.4$.
So we can conclude the height of the porch is given by $h\approx 3.4$ ft.
-
Figure out the length of the side $x$.
HintsHere you see the law of sines.
Here you see the law of cosines.
SolutionLet's start with the triangle on the left and proceed to the right.
- The following values are known: two angles, $30$° and $70$°, and the side of length $10$ opposite the angle of $30$°. We use the law of cosine: $\frac{10}{\sin(30°)}=\frac{x}{\sin(70°)}$. Multiplying both sides by $\sin(70°)$ gives us $x=\frac{10}{\sin(30°)}\times \sin(70°)\approx 18.8$.
- We know the angle $75$° opposite to the unknown side and the two other sides, $7$ and $5$. So we use the law of cosines: $x^2=7^2+5^2-2(7)(5)\cos(75°)$. Using PEMDAS we get $x=49+25-70(0.2588)=55.9$ and taking the square root leads to $x\approx7.5$.
- Here we know two angles, $65°$ and $72°$, and the side of length $12$ opposite the angle $65$°. We use the law of cosine: $\frac{12}{\sin(65°)}=\frac{x}{\sin(72°)}$. Multiplying with $\sin(72°)$ gives us $x=\frac{12}{\sin(65°)}\times \sin(72°)\approx 12.6$.
- For the last triangle we use the law of cosines again. We know the angle $62$° opposite to the unknown side and the two other sides, $8$ and $3$. $x^2=8^2+3^2-2(8)(3)\cos(62°)$. Using PEMDAS we get $x=64+9-48(0.4694)=50.5$ and taking the square root leads to $x\approx7.1$.
-
Clarify the law of sines.
HintsIf you know two angles and the length of one of the sides opposite one of these angles, then you can determine the length of the side opposite to the other angle.
For the given pictured situation you can conclude
$\frac{15}{\sin(96.77°)}=\frac{c}{\sin(33.23°)}$.
Each time the side is written in the numerator.
SolutionThe law of sines states that the ratio of any side and the sine of the opposite angle is the same as the ratio of any of the other side and the sine of its opposite angle.
We can write it is as follows
$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}$.
Pictured beside we have an example; the law of sines tells us that
$\frac{15}{\sin(96.77°)}=\frac{c}{\sin(33.23°)}$.
-
Examine the height of the tower.
HintsThe law of cosines is given by
$a^2=b^2+c^2-2bc\cos(A)$,
where $A$ is the angle opposite to the side $a$.
Pay attention to PEMDAS; first multiply or divide, then add or subtract.
You first have to calculate $2bc\cos(A)$ and then subtract the resulting product after.
Don't forget to take the square root.
SolutionAll we know is given in the picture beside.
We know two sides, $420$ yds and $400$ yds, as well as one angle, $3$°. The side opposite to this angle is wanted. Thus we take the law of cosines:
$~$
$\begin{array}{rclll} x^2&=&~(420)^2+(400)^2\\ & &~-2((420)(400))(\cos(3°)) \end{array}$
$~$
Using PEMDAS we can simplify as follows:
$\begin{array}{rclll} x^2&=&~176400+160000-336000(0.9986)\\ &=&~860.5 \end{array}$
$~$
Last we take the square root to get $a\approx 29$.
So we can conclude the height of the tower by $29$ yds.