Triangle Review

Basics on the topic Triangle Review
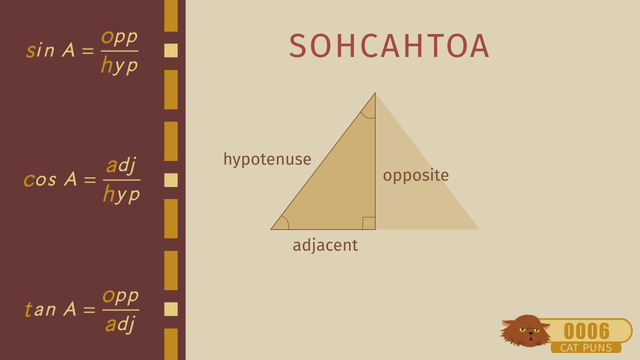
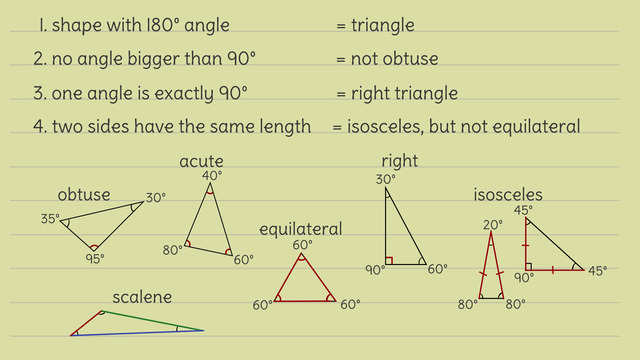
A triangle is polygon with three edges and three vertices. It has three angles, which always add up to 180º. A triangle can be equilateral, isosceles, or scalene when classified according to its side lengths and can be acute, right, or obtuse when classified according to its angles.
An equilateral triangle has three equal sides, an isosceles triangle has two equal sides, and a scalene triangle has no equal sides.
An acute triangle has three acute angles, a right triangle has one right angle and two acute angles, and an obtuse triangle has one obtuse angle and 2 acute angles.
An equilateral triangle is equiangular, meaning that each angle is the same; the angles of an equilateral triangle are all 60º.
An isosceles right triangle has two equal sides and one right angle. Thus, the three angles in an isosceles right triangle are 45º, 45º, and 90º.
Classify two-dimensional figures into categories based on their properties.
CCSS.MATH.CONTENT.5.G.B.3
Transcript Triangle Review
Sherlock Bones is on a new case… Old Lady Miller was mugged, and a very precious item was stolen! It all happened so fast... she doesn’t remember much, but she does remember the image of a polygon with three sides and three angles. Bones, the super sleuth, knows right away that the shape she describes is a triangle, and the interior angles sum to 180-degrees. But that's not enough information to solve the crime, so…
Categorizing Triangles
Sherlock Bones hypnotizes Old Lady Miller and uncovers three more very important details: First, the triangle shape has no angles larger than 90°. From this, Bones concludes the wanted triangle cannot be obtuse because an obtuse triangle contains an angle that's greater than 90°. Second, there's one 90° angle, so Bones knows the triangle has to be a right triangle. The last detail: exactly two sides of the triangle have the same length, so he knows it must be an isoceles triangle, not an equilateral. Will these clues help him find the mugger? I sure hope so!
Bones tries to recall all the different types of triangles, but the situation is getting out of control. Let's help Bones organize the characteristics of these three-cornered shapes. Triangles can be categorized by their angles or their side lengths. Obtuse triangles have one angle greater than 90°. Acute triangles have all angles less than 90°, equilateral triangles have all angles measuring 60° and right triangles have exactly one 90° angle.
Categorizing triangles by their side lengths is just two sides of the same coin. In a triangle, the bigger the angle measure, the longer the side length. None of the sides of a scalene triangle are the same. Isosceles triangles have at least two sides that are the same length while all sides of an equilateral triangle are the same. This means that some triangles may fit into more than one category. This is not the news Bones wants to hear. Bones has a list of five suspects that may fit the description. Can he identify the thief with these clues?
Analyzing different Triangles
He uses the process of elimination to rule out the suspects one by one. The first suspect has a triangle shape on his tie: One angle has a measurement of 110° – this is clearly larger than 90°, making this an obtuse triangle. Before Bones releases this suspect, he double checks the shape with the clues. The triangle cannot contain a 90° angle because if one angle is greater than 90°, the sum of all three angles will be greater than 180°. Also, although two sides of the triangle have the same length, the triangle is an isosceles triangle but not equilateral triangle which has three equal sides. Bones releases this suspect.
The second suspect in the line-up has a triangle-shaped goatee. His facial fuzz is the same length on all three sides, so all three angles are equal to 60°, and the triangle is acute - not an obtuse or right. Plus, not only is the triangle an isosceles triangle, but it's also an equilateral triangle. Sherlock lets this suspect walk.
The third suspect has a triangle pendant on her necklace. The pendant has an angle measuring 50°. Since the angle is less than 90°, the shape is an acute triangle, not a right or an obtuse triangle. Since the other two angles are the same, they measure 65°, the two corresponding sides must have the same length. The triangle pendant is in the shape of an isosceles triangle - not an equilateral, so this suspect is not the guilty party.
The fourth suspect sports a triangle hair...band...thing. The side lengths of the shape are all different, so it's a scalene triangle, not an isosceles triangle. This woman isn't a thief. She gets to fly the coop, too.
The last suspect has a triangle handkerchief in his jacket pocket. Bones knows that two of the angles measure 45°, so the missing angle is 90°, this shape is definitely a right triangle – not obtuse. So far, so good. Because the two angles are equal, the two corresponding sides have the same length, so this shape is an isosceles triangle – not an equilateral.
It's incredible! Bones has the evidence to prove the crime, so the thief will have to do the time! Are you wondering what the thief stole from the old lady? He stole her heart.
Triangle Review exercise
-
Classify the different triangles.
HintsWrite down the properties that can be used to classify triangles into the following types:
- Acute, obtuse, or right
- Equilateral, isosceles, or scalene
An obtuse triangle must have one angle that is greater than $90$°.
All three sides of an equilateral triangle are the same length.
SolutionLet's review the types of triangles.
Triangles can be classified based on their angles. Every triangle will have two acute angles. The third angle is what sets the different types of triangles apart from each other.
If the third angle is acute, the triangle is called an acute triangle. If the third angle is $90$°, or a "right" angle, the triangle is called a right triangle. If the third angle is obtuse, the triangle is called an obtuse triangle.
Triangles can also be classified based on how many sides are equal in length. If all sides are equal in length, the triangle is equilateral. If two sides are equal in length, the triangle is isosceles. If all three sides are different in length, the triangle is scalene.
Each triangle can be classified both by its side lengths, and by its angle. For example, a triangle that has one obtuse angle, and in which all side lengths are different, is called an obtuse scalene triangle.
Now let's look at the information provided in the question:
A polygon with three sides and three angles must be a triangle.
If no angles are greater than $90$°, the triangle cannot have an obtuse angle. This means that it cannot be an obtuse triangle.
If one angle in the triangle is equal to $90$°, we can classify it as a right triangle based on this angle. As a side note, the angles of a triangle must sum to $180$°, so the remaining two angles of this right triangle must sum to exactly $90$°.
If exactly two sides of the triangle have the same length, then it is an isosceles triangle.
-
Decide if the suspect is the thief.
HintsAn obtuse triangle has one angle that is greater than $90$°.
A right triangle has one angle that is exactly equal to $90$°.
All four clues will match the pendant if this suspect is the thief.
SolutionLet's look at the four clues and see if the properties of the suspect's pendant match each one:
Clue 1: The thief has a triangle somewhere in their outfit. This suspect's pendant is a triangle, because it has three sides and three angles. Therefore the pendant matches clue 1. ✓
Clue 2: The triangle on the thief's outfit is not an obtuse angle. The pendant's three angles are $\angle A = 50$° and $\angle B = \angle C = 65$°. None of the angles are greater than $90$°. This means that the pendant does not contain an obtuse angle. So the suspect's pendant matches clue 2. ✓
Clue 3: The triangle on the thief's outfit is a right triangle. None of the angles in the pendant are equal to $90$°. This means that the pendant does not contain a right angle and does not match clue 3. ✗
Clue 4: The triangle on the thief's outfit is isosceles, but not equilateral. For a triangle to be isosceles, two (and only two) of the sides must be equal in length. Exactly two side lengths of the pendant are equal, which means it is an isosceles triangle. So the pendant matches clue 4. ✓
Overall, the pendant matches exactly three of the four clues. The suspect cannot be the thief, because there is a clue that does not match with the suspect's outfit.
-
State what kind of triangle appears in each flag.
HintsIf the sides of a triangle are marked the same (for example, two sides both have a single mark through them), then those sides are equal in length.
If all three sides of a triangle have a different number of marks on them, then all sides are different in length.
Each triangle can be classified both using its side lengths, and using its angles.
SolutionLet's quickly review how we can classify triangles using their side lengths, and angles.
All three sides are the same length $\rightarrow$ equilateral
Two sides are the same length $\rightarrow$ isosceles
Each side is a different length $\rightarrow$ scalene
No angles are greater than $90$° $\rightarrow$ acute
One angle is equal to $90$° $\rightarrow$ right
One angle is greater than $90$° $\rightarrow$ obtuse
In the first triangle, all side lengths are equal. This means that it must be an equilateral triangle. All angles are equal to $60$°. Therefore all angles are less than $90$° and the triangle is also acute.
The next triangle has two side lengths that are equal, and one that is different. This means that it is an isosceles triangle. The angles measure $75$°, $75$°, and $30$°. Therefore no angles are equal to or greater than $90$°, and the triangle is acute.
The third triangle has no sides that are equal in length. This means that it must be scalene. It also has one $90$°, or right, angle. Therefore it is a right triangle.
The last triangle has three sides that differ in length. Therefore it is scalene. It also has one angle ($100$°) that is greater than $90$°. Therefore it is obtuse.
-
Identify the bank robber's safe house.
HintsRemember that the angles in a triangle must always sum to $180$°.
An obtuse triangle contains one angle that is greater than $90$°.
You can re-arrange the equation:
$\angle A + \angle B + \angle C = 180°$
To solve for an unknown angle, given the values of the other angles.
All angles in an equilateral triangle are equal to $60$°.
SolutionWe know that the safe house roof is in the shape of an obtuse triangle, meaning that one of its angles is greater than $90$°. Let's solve for the missing angles, and see if any of these houses match that description.
First, we know that all angles in a triangle must sum to $180$°. We can write this as:
$\angle A + \angle B + \angle C = 180°$
In this question, we typically know two of the angles in a triangle, and we need to solve for the third angle. We can rearrange our equation to put a single angle on the left hand side.
$\begin{array}{rcl} \angle A + \angle B + \angle C & = &180°\\ \color{#669900}{-\angle B - \angle C} & &\color{#669900}{-\angle B - \angle C}\\ \angle A & = & 180° - \angle B - \angle C \end{array}$
Now let's solve for the missing angle on each roof, and see if any of the angles are obtuse.
For the first house, we know that one angle is right, or $90$°, and another is $45$°. We can determine the third angle using the equation we just found:
$\angle A = 180° - \angle B - \angle C$
$\angle A = 180° - 90° - 45°$
$\angle A = 45°$
Therefore all angles in the first house's roof are acute.
The second house has an angle equal to $45$°, and another equal to $50$°. Using the same equation as above, we can find that the third angle is equal to $85$°. This means that all angles on the second house's roof are acute.
The third house has two angles equal to $35$°. Similarly, we can find that the third angle is $110$°. This means that this roof contains an obtuse angle. This could be the safe house!
The fourth house is in the shape of an equilateral triangle. We therefore know that all angles are equal to $60$°. Therefore it is an acute triangle.
The fifth house has one angle equal to $50$°, and another equal to $65$°. Similarly to the first roof, we can find the third angle to be $65$°.
Therefore only the third house has a roof that is in the shape of an obtuse triangle.
-
Identify the true statements about triangles.
HintsAcute angles are less than $90$°. Obtuse angles are greater than $90$°.
The sum of all angles in a triangle must be equal to $180$°.
An obtuse triangles has one angle greater than $90$°. Since the sum of all the angles must be equal to $180$°, the sum of the other two angles must be less than $90$°.
Equilateral triangles are a special case of isosceles triangles.
SolutionThe bigger the value of an angle within a triangle, the longer the corresponding side length will be. ✓
The side opposite an angle in a triangle is known as the corresponding side. In general, when an angle in a triangle is larger, the corresponding side will be longer. The angle "points" to the two ends of its corresponding side. If the angle is larger, the two ends of the corresponding side will be farther apart. This means that the side will be longer.
Each angle in an acute triangle must be less than $90$°. ✓
An acute triangle can only contain acute angles. So all angles in an acute triangle must be less than $90$°.
The sum of the angles in a triangle will always be less than $180$°. ✗
The sum of the angles in a triangle must always be equal to $180$°. Therefore this sum can never be less than $180$°.
An obtuse triangle has two acute angles. ✓
The sum of the angles in a triangle must always be equal to $180$°. An obtuse triangle has one obtuse angle. We can show these two properties mathematically:
- $\angle A + \angle B + \angle C = 180$°
- $\angle A \gt 90$°
$\begin{array}{rcl} \angle A + \angle B + \angle C & = &180°\\ \color{#669900}{-\angle B - \angle C} & &\color{#669900}{-\angle B - \angle C}\\ \angle A & = & 180° - \angle B - \angle C \end{array}$
We can substitute this new expression for $\angle A$ into equation (2) to get:
$\begin{array}{rcl} 180° - \angle B - \angle C & \gt & 90°\\ \color{#669900}{+\angle B + \angle C - 90°} & &\color{#669900}{+\angle B + \angle C - 90°}\\ 180° - 90° & \gt & \angle B + \angle C\\ 90° & \gt & \angle B + \angle C \\ \end{array}$
So the sum of angle $B$ and angle $C$ is less than $90$°. Therefore they are both acute angles.
All isosceles triangles are also equilateral triangles, but not all equilateral triangles are isosceles. ✗
Two sides of an isosceles triangle are equal in length. All three sides of an equilateral triangle are equal in length. Therefore an equilateral triangle will also have two sides that are equal in length. This means that equilateral triangles are also isosceles triangles. However, an isosceles triangle can have two sides that are equal, and a third side that is of a different length. This shows that a triangle can be isosceles without being equilateral.
Two of the angles in an isosceles triangle are equal. ✓
Isosceles triangles have two sides that are equal, and two angles that are equal.
-
Determine which portions of the statements are incorrect.
HintsRead these statements slowly and carefully. They all have some truth in them, but some have one or two details that are incorrect.
It may help to write down all the rules you know about the types of triangles that are discussed in each statement before reading the full statement. Then you can compare things you know to be true against the details of each statement.
Solution1.$~$An obtuse triangle has one angle greater than $90$°. We know that the sum of the angles in the triangle must be $180$°. So the sum of the two remaining angles must be less than $90$°.
2.$~$An isosceles triangle has two sides that are of equal length. An equilateral triangle has three sides that are of equal length. So you can choose any two sides on an equilateral triangle, and they will be equal in length. This means that equilateral triangles are all isosceles triangles. However, an isosceles triangle can have two sides that have equal lengths, and a third side with a different length. Therefore only some isosceles triangles are equilateral.
3.$~$An obtuse triangle has one obtuse angle. The sum of the angles in a triangle must be $180$°. If one angle is greater than $90$°, the sum of the other two angles must be less than $90$°. That is the only way for all angles to sum to $180$°. If the sum of the two remaining angles is less than $90$°, each of these angles must be less than $90$°. So both the remaining angles must be acute.
4.$~$The sum of the angles in a triangle must always be equal to $180$°.
5.$~$A right triangle has one angle that is equal to $90$°; the other two angles must always be acute:
$\angle A + \angle B + \angle C = 180°$
Setting $\angle A = 90°$...
$\begin{array}{rcl} 90° + \angle B + \angle C & = & 180°\\ \color{#669900}{-90°} & &\color{#669900}{-90°}\\ \angle B + \angle C & = & 90°\\ \end{array}$
We know that $\angle B$ and $\angle C$ must both be positive, and neither can be equal to zero. We now also know that $\angle B$ and $\angle C$ must sum to $90$°. Therefore they each must be less than $90$°, and are both acute.
6.$~$Two important characteristics of an isosceles triangle are: a) two of the sides are equal in length, and b) two of the angles are equal.