Special Triangles

Basics on the topic Special Triangles
Two special right triangles are the 30-60-90 and the 45-45-90 triangles.
For a 30-60-90 triangle, the ratios of the side lengths are 1:√3:2. The smallest side is opposite 30º while the longest side, or hypotenuse, is opposite 90º. In a 45-45-90 triangle, the ratio of the side lengths are 1:1:√2. The longest side, or hypotenuse, is opposite 90º. When solving for the missing length of a side of a special right triangle given the length of one of its sides, use the Pythagorean Theorem and take note of the relevant side ratio to use.
A knowledge of special triangles has several applications in engineering works and construction.
Define trigonometric ratios and solve problems involving right triangles.
CCSS.MATH.CONTENT.HSG.SRT.C.8
Transcript Special Triangles
Grandpa Lindbergh looks at old photos and thinks about the past… Back in the day, he was a famous aviator. He sees a picture of an old friend. Oh boy, did they have some exciting times together. Grandpa wonders how his friend is doing now.
Suddenly, sick and tired of just sitting in his rocking chair and thinking back to his glory days, Grandpa decides to go on an expedition. He can visit an old friend. He packs up his things and gets his favorite girl ready to go – a double-decker named Kittyhawk. Off he goes into the wild, blue yonder.
Special Triangles
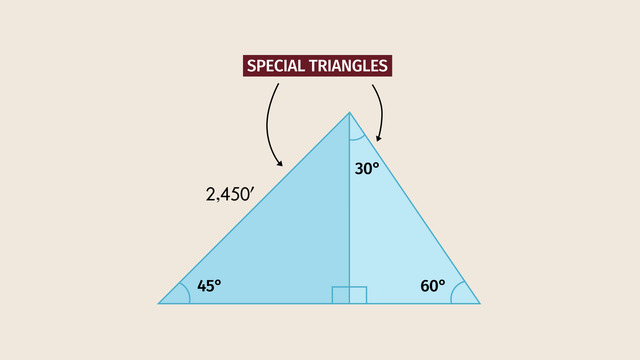
So far, the flight seems to be going well. Grandpa checks the plane’s flying angle: 45° and a distance of 2,450 feet. It’s all A-Okay. Wait. What’s that noise? Something is wrong. The engine just died, and he's falling at a 60° angle to the horizon! Oh no! Now the instrument panel is dead! Grandpa will have to crash land the plane.
How can we figure out Grandpa's location to rescue him? To figure this out, we can use special triangles. Let’s review what we know. Before the engine conked out, he flew at an angle of 45° and traveled 2,450 feet. After the engine blew, he fell at a 60° angle to the horizon. Let’s graph this. The angle next to the 60° falling angle equals 30°. As you can see, we divided the large triangle into two right triangles. The two right triangles are special triangles.
Iscoceles Triangles
First, let’s analyze the special triangle on the left. This left triangle has two 45° angles, so it's an iscoceles right triangle. How do we know this? There are 180° in a triangle, so do the math. If both angles have the same measurement then the legs opposite the angles also have the same measurement or length. Let’s add some labels, length 'a' goes here and here, and for the hypotenuse, we'll label it length 'c'.
We can use the Pythagorean Theorem to solve for the unknown measurement. For this special triangle, we get the equation c² = a² + a². By simplifying the right side of the equation and taking the square root on both sides of the equation, we get 'c' equals the square root of 2a². To calculate a square root of a product you can also calculate the product of the square root of each factor and simplify as far as possible. The hypotenuse of this special triangle is equal to 'a' times the square root of 2.
Now, let's apply this knowledge to Grandpa's problem. Since we know 'a' times the square root of 2 is equal to 2,450, we can solve for the variable 'a'. To make things easier, we'll round all numbers to the nearest whole number. The two equal legs have a length of 1,732 feet.
Equilateral Triangles
Okay, that's one down. Now, let’s work on the special triangle on the right. This is a 30-60-90 triangle. To help you to understand 30-60-90 triangles, lets draw an equilateral triangle. We'll label the length of each equal side as 2a. Now, as you can see the altitude splits the equilateral triangle into two 30-60-90 triangles. The base of each 30-60-90 triangle is equal to 'a'.
Now, let's apply this knowledge of 30-60-90 triangles to solve Lindbergh’s problem. We know the hypotenuse has a length of 2a, and the leg opposite the 30-degree angle has a length of 'a'. Let's call the third leg 'b'. We can use the Pythagorean Theorem to determine the length of the third leg with regard to 'a'. We get the equation (2a)² = a² + b².
Simplifying the left side of the equation we get 4a² = a² + b². Now we can subtract a² on both sides of the equation, what leaves 3a² = b². Last taking the square root on both sides we get the root of (3a²) = b². Again, we can split up the left side, calculating the product of the square root of each factor. we get the root of 3 times the root of a² =b , so the leg opposite the 60° angle is equal to 'a' times the square root of 3, and since we already know that leg is equal to 1732 feet, we can solve for 'a' and calculate the other lengths. Remember to round to the nearest whole number. The hypotenuse of the 30-60-90 triangle is equal to 2,000 feet, and Grandpa Lindbergh traveled a total distance of 2,732 feet.
With no instruments, he managed the crash landing. That old guy is really something else! Is that Grandpa's friend!!?
Special Triangles exercise
-
Solve for the height and distance travelled on land of the plane.
HintsThe square root of a product is the product of the square roots of its factors:
$\sqrt{a\times b}=\sqrt a \times \sqrt b$.
The Pythagorean theorem says that the sum of the squares of both legs of a right triangle is the same like the square of the hypotenuse.
An iscoceles triangle is one where two of its sides have the same length, while an equilateral triangle is one where all of its sides have the same length.
SolutionWe are finding the base and height of an iscoceles right triangle: it has two angles of 45°, meaning that their opposite legs have the same length.
So the hypotenuse is $c$ and both legs are $a$. Using the Pythagorean theorem, we get:
$c^2=a^2+a^2=2a^2$
Taking the square root of both sides, we get:
$\sqrt{c^2}=\sqrt{2a^2}$
which is equivalent to
$c=\sqrt 2 ~ a$
as the square root of a product is the product of the square roots of its factors.
Plugging in the known value for $c=2450$, we get $2450=a~\sqrt 2$.
And dividing by $\sqrt 2$ gives us $a=1,732.4\approx 1,732$ feet.
-
Calculate the distance Grandpa Lindbergh's plane will fall.
HintsThe square root of a product is the product of the square roots of its factors.
The Pythagorean theorem says that the sum of the squares of both legs of a right triangle is the same like the square of the hypotenuse.
SolutionWe can think of an equilateral triangle as two 30-60-90 triangles, as pictured to the right. So if the sides of the equilateral triangle are $2a$, then the hypotenuse of the 30-60-90 triangles is $2a$ and their base is $a$. Let's call the height $b$.
We can use the Pythagorean theorem to get $(2a)^2=a^2+b^2$. To square a product, we square each factor:
$4a^2=a^2+b^2$.
Subtracting $a^2$ from both sides leads to $3a^2=b^2$.
Next we take the square root of both sides to get:
$\sqrt {3a^2}=\sqrt {b^2}=b$.
On the left-hand side we take the square root of each factor:
$\sqrt 3~ a=b$.
$b$ is the height of the plan before falling down, namely $b=1,732$.
So we have to solve the following equation:
$\begin{array}{rcl} \sqrt 3~a& = & ~1,732\\ \color{#669900}{\div\sqrt 3} & & \color{#669900}{\div\sqrt 3}\\ a & = & 1000 \end{array}$
Multiplying $a$ by $2$, we get that the distance Grandpa Lindbergh's plane will fall is 2000 feet.
-
Determine the length of the missing side.
HintsUse the Pythagorean theorem: the sum of the squares of both legs of a right triangle is the same like the square of the hypotenuse.
Determine the hypotenuse: the side opposite the right angle.
For this example, the Pythagorean theorem says that $a^2=b^2+c^2$.
SolutionFor each right triangle, use the Pythagorean theorem to find the length of the missing side:
- Let's start with the green triangle: here we are missing the hypotenuse, $a$. The Pythagorean theorem gives us $a^2=3^2+4^2=9+16=25$, and taking the square root leads to $a=\sqrt{25}=5$.
- Next the blue one with missing leg $c$. The hypotenuse has length $10$. Thus, $10^2=8^2+c^2$, which is equivalent to $100=64+c^2$. Subtracting $64$ from both sides and taking the square root leads to $c=\sqrt{36}=6$.
- Now for the red triangle, with missing hypotenuse, $d$. We have that $d^2=4.5^2+6^2=56.25$. Taking the square root gives us $d=7.5$.
- The last triangle is the yellow one, with a missing leg length $b$ and a hypotenuse length of $17$. This gives us $17^2=15^2+b^2$. Subtracting $225$ from both sides gives us $64=b^2$, and thus that $b=\sqrt{64}=8$.
-
Find the distance Grandpa Lindbergh has to fly to get to a height of 1500 feet.
HintsDecide if the missing side is the hypotenuse or not.
Use the Pythagorean theorem: square each leg of a right triangle and add them together to get the square of the hypotenuse.
SolutionLook at the triangle to the right, with the missing hypotenuse $c$ and the legs of length 1500.
Using the Pythagorean theorem, we get:
$c^2=1500^2+1500^2=2\times 1500^2$
So $c^2=4500000$.
Taking the square root of both sides gives us the solution:
$c=\sqrt{4500000}=2,121.32$
Rounding the result gives us a distance of
2,121 feet in which Grandpa Lindbergh needs to fly to get to a height of 1500 feet.
-
State what a triangle with two 45° angles is called and what is special about it.
HintsAll angles of an equilateral triangle are equal.
The sum of all the angles of any triangle is always 180°.
The opposite legs of equal angles have equal lengths.
SolutionAny triangle with two 45° angles is an iscoceles right triangle.
We can see this in the following way:
- The sum of the three angles of any triangle is always 180°.
- Thus, if two angles are 45°, the last angle must be $180^\circ - (45^\circ+45^\circ)=90^\circ$.
- Also, the triangle legs opposite to the 45° angles have equal lengths.
-
Calculate the length of the wooden slats needed to build the kite.
HintsIn an iscoceles right triangle, two legs have the same length and the third leg is the hypotenuse.
You have to use the Pythagorean theorem twice.
Keep in mind that in a 30-60-90 triangle the leg opposite to the right angle is double as long as the this one opposite the 30° angle.
SolutionFirst, we take a look at the isosceles right triangles on top. We know the length of the hypotenuse and thus we can use the Pythagorean theorem, where $a$ is the missing length:
$12^2=2a^2$.
Dividing by $2$ we get $a^2=72$, and so $a=\sqrt{72}=8.485...\approx 8.5$.
We still need the length of the longer part of the middle axis, $b$, of the kite.
We use the Pythagorean theorem, as well as the fact that the hypotenuse is twice as long as $a$: $2\times 8.5=17$.
We then have that:
$17^2=8.5^2+b^2$.
Subtracting $72.25$, we get $b^2=216.75$ and thus $b=\sqrt{216.75}=14.72...\approx 14.7$.
And so we know that the horizontal wooden slat much be $2\times 8.5=17$ inches, and the length of the vertical wooden slat must be $8.5+14.7=23.2$ inches.
All together, the total amount of wood needed is $40,2$ inches.