From the Pythagorean Theorem to the Distance Formula

Basics on the topic From the Pythagorean Theorem to the Distance Formula
After this lesson, you will be able to derive the Distance Formula from the Pythagorean Theorem and use the Distance Formula to find the distance between two points. The lesson begins by teaching you to visualize a distance between two points in the coordinate plane as the hypotenuse of a right triangle. It leads you to learn that the legs of the right triangle are found by subtracting the ‘x’ or ‘y’ coordinates of the points. It concludes with using the Pythagorean Theorem to find the hypotenuse and develop the Distance Formula. Learn about the Distance Formula by helping the villagers and dragons of Nanjie find their way to the temple!
This video includes key concepts, notation, and vocabulary such as the Pythagorean Theorem (the sum of the squares of the legs of a right triangle equal the square of the hypotenuse); and points in the coordinate plane (each point consists of an x and y value); and the Distance Formula (the formula which allows us to plug in the coordinates of two points and get the distance between them). Before watching this video, you should already be familiar with the Pythagorean Theorem and graphing points in the coordinate plane. After watching this video, you will be prepared to learn how to use the Distance Formula to find the distance between any two points in the coordinate plane. Common Core Standard(s) in focus: 8.G.B.8 A video intended for math students in the 8th grade Recommended for students who are 13 - 14 years old
Transcript From the Pythagorean Theorem to the Distance Formula
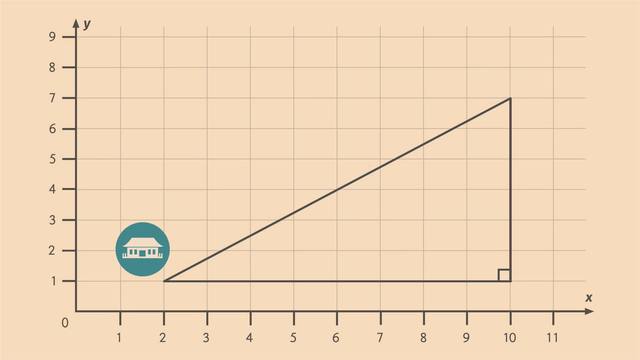
In honor of the magnificent dragons that have brought them good fortune, the hospitable villagers of Nanjie have built a glorious temple on a hill. They begin their grand parade from Nanjie to the base of the temple hill. The villagers must walk around the lake to get there but the dragons can fly there directly. In order to calculate their travel distances, we'll discover how we go from the Pythagorean Theorem to the Distance Formula. Let's look at the route on a coordinate plane, where each unit represents 1 kilometer. The village is at point 'B.' The base of the temple hill is at point 'A.' When the villagers walk around the lake to the base, they turn at point 'C.' How far must the villagers walk? By counting from 2 to 10 we can see this distance is 8 kilometers long. By counting from 1 to 7 we can see this distance is 6 kilometers long. In total, the villagers must walk 14 kilometers to reach the base of the hill. The dragons have a much shorter journey from point 'B' to the base of the hill, point 'A.' But we CAN'T easily count the squares of this diagonal on the coordinate plane. Therefore, to find this distance, we need to use our spatial knowledge that comes from geometry. Can you see a familiar shape in this diagram? This shape is, in fact, a right triangle. What formula do you know that relates the sides of a right triangle? The Pythagorean Theorem states that when a triangle is a right triangle the square of its hypotenuse is equal to the sum of the squares of the other two sides. We can write this algebraically. Given two legs, 'a' and 'b,' and the hypotenuse, 'c' then 'a' squared, plus 'b' squared, equals 'c' squared. Since we're solving for 'c,' let's use the symmetric property of equality to move 'c' squared to the left side. Now let's substitute our known values for 'a' and 'b' into the equation then square them. "Which gives us 'c' squared is 64 plus 36." So, 'c' squared is 100. To solve for 'c', we take the square root of both sides. We can solve this by asking, "what number times itself is 100?" The answer is 10. That means the dragons only have to fly 10 kilometers to get to the base of the hill! We can use this method to find the distance between ANY two points in the coordinate plane. Let's review our calculations to derive the distance formula. Given the two points (x1, y1) and (x2, y2) we found the distance of this HORIZONTAL leg, 8, by calculating x2 minus x1 and we found the VERTICAL leg of the right triangle, 6, by calculating y2 minus y1. Now, let's substitute our terms into the Pythagorean Thereom. That's the difference of the x-values for 'a' and the difference of the y-values for 'b'. Let's call the hypotenuse 'd,' for distance. We solve for 'd' by taking the square root of both sides. This leaves us with the distance formula: 'd' equals the square root of the quantity, x2 minus x1 squared, plus the quantity, y2 minus y1 squared. We can use the distance formula to find the distance between ANY two points. Now let's find the length between point one (8,3) and point two (9,5). First, label our points with (x1, y1) and (x2, y2). Then, let's substitute these values into the formula. The difference in the x-values is one and the difference in the y-values is two. So, 'd' is the square root of 1 plus 4. That gives us the distance is the square root of 5. We can write our answer as this or we can think about the perfect squares around five and use them to get an approximation. So, we have the square root of 4 is less than the square root of 5, which is less than the square root of 9. Infact, there are five square roots of whole numbers from the square root of 4 to the square root of 9. So if we were to divide this up evenly we can say the square root of 5 is approximately 2.2. And before the dragons and the villagers start celebrating at the temple let's review how we got from the Pythagorean Theorem to the Distance Formula. The Pythagorean Theorem describes the relationship between the LEGS of a right triangle and the HYPOTENUSE; that's 'a' squared, plus 'b' squared, equals 'c' squared. In the coordinate plane, the distance between two points could be viewed as the HYPOTENUSE of a right triangle and the LEGS of the triangle are calculated by finding the difference between the x-values and the difference between the y-values. We solve for 'd' by taking the square root of both sides. This is the distance formula, which we can use to find the distance between any two points in the coordinate plane. Thanks to the distance formula, the dragons and the villagers have all arrived at the temple. Let the celebration begin!











