Finding Trigonometric Ratios

Basics on the topic Finding Trigonometric Ratios
Summary of Finding Trigonometric ratios
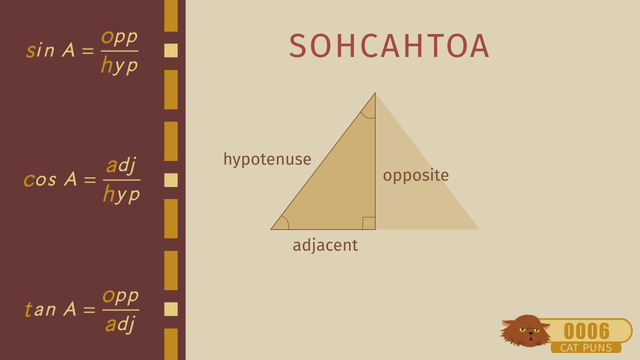
Trigonometric ratios are special measurements of a right triangle – a triangle with one angle measuring 90 degrees. There are three basic trigonometric ratios: sine (sin), cosine (cos), and tangent (tan).
Given a right triangle, the trigonometric ratios of either of the angles θ which are not 90 degrees can be found by using the following formulas:
- Sine: (sin) θ = Length of the leg opposite to the angle (O) / Length of the Hypotenuse (H)
- Cosine: (cos) θ = Length of the leg adjacent to the angle (A) / Length of the Hypotenuse (H)
- Tangent: (tan) θ = Length of the leg opposite to the angle (O) / Length of the leg adjacent to the angle (A)
The symbol “θ” is the Greek letter “theta”, and is often used to represent angles. The mnemonic device “SOH-CAH-TOA” is used to remember the formulas more easily: “SOH” means Sine; Opposite over Hypotenuse, “CAH” means Cosine; Adjacent over Hypotenuse, and “TOA” means Tangent; Opposite over Adjacent.
Trigonometric ratios not only help in finding unknown angles of a right triangle, but can also be used to find unknown angles of other types of triangles as well as in practical scenarios, like finding the height of tall towers or buildings. Like, the height of the Eiffel Tower: once you know your distance from the base of the tower and the angle of elevation of your sight to the top most part of the tower, then you can compute the height of the tower using trigonometric ratios.
Define trigonometric ratios and solve problems involving right triangles.
Common Core Standard
CCSS.MATH.CONTENT.HSG.SRT.C.6
Finding Trigonometric Ratios Exercises
Transcript Finding Trigonometric Ratios
Let me tell you a tail of the Pharaoh SOH-CAH-TOA. To honor Pharaoh SOH-CAH-TOA, a huge PURR-amid...pyramid was constructed. The pharaoh, who is paw-sitively crazy for cats, ordered a pyramid from the pyramid-building company, Cleo-CAT-ra, for his cat to live in since pyramids are the PURR-fect shape. To determine the dimensions of the miniature pyramid, we gato use trigonometric ratios.
Three Trig Ratios
Let’s review the ratios to help the Pharoah so we can help him avoid a cat-astrophy. For right triangles, the most common trig ratios are sine, cosine and tangent. Let’s take a look at the three ratios. You should remember that the sine of ∠A is the length of the opposite side divided by the length of the hypotenuse. The cosine of ∠A is the length of the adjacent side divided by the length of the hypotenuse. And finally, the tangent of ∠A is the length of the opposite side divided by the length of the adjacent side.
You won’t believe this, but the pharaoh’s name is a mnemonic device we can use to remember these three trig ratios! Let's paws and have a look: SOH, CAH, TOA. It’s easy to get confused about which side is which. The hypotenuse is always located opposite the right angle. The other two sides are named depending on the angle in question. The opposite side is across from the target angle and the adjacent side is between the target angle and the right angle.
Calculating Trig Ratios
The Pharoah is not kitten around. Since he already knows the trig ratios, he can figure out the trig ratios for his pyramid by using the measurements he knows. Look at the triangle face of the pyramid. Dividing a side of the base by 2 and drawing in an altitude gives us two right triangles. Since each side of the base is 755 ft we can divide the base by 2, to calculate the length of the side adjacent to ∠A. Now we know all three lengths: The length adjacent to ∠A is 377.5 feet. The length of the hypotenuse is 610 feet, and the length opposite ∠A is 479.16 feet. Let's calculate the trig ratios!
To calculate the sine of an angle, simply divide the length of the opposite side, 479.16, by the length of the hypotenuse, 610. To get the cosine, divide the length of the adjacent side, 377.5, by the length of the hypotenuse, 610. And last, but not least, divide the length of the opposite side, 479.16, by the length of the adjacent side, 377.5, to get the tangent.
Calculating the side lengths with given trig ratios
Now the pharaoh can use this information to calculate the measurements for the miniature pyramid. Because the kitty cats' pyramid will be a similar version of the pharaoh's, the trig ratios will be the same. If the miniature will have a height of 20 feet, what are the other lengths? Chose the trig ratio that will help you to calculate the unknown length with the fewest steps.
Let's use the tangent ratio, which is 1.269, to set up a proportion using 20 as our opposite side length. Now we have to *solve for the adjacent side. Using opposite operations and isolating our variable, we find that the adjacent side is equal to 15.76 feet. This is just half the base of the face of the pyramid, so we multiply by 2 to determine the full length of the base. Pharoah SOH-CAH-TOA's looks at the plans he's feline pretty good about the mini pyramid right about now!
The Pharoah is speechless! I guess the cat's got his tongue! Ugh...All these cat puns are freakin' meowt
Finding Trigonometric Ratios exercise
-
Determine the trigonometric ratios of the pyramid.
HintsThe Pharoah's name, SOHCAHTOA, is a mnemonic device that helps us remember the trig ratios for $sin$, $cos$, and $tan$. It breaks into three parts, one for each trig ratio:
SOH, CAH, and TOA.
S represents sin, C represents cos, and T represents tan. O represents the side length Opposite to the angle, A represents the side length Adjacent to the angle, and H represents the hypotenuse.
The trigonometric ratios, or trig ratios, can be applied to right triangles.
The mnemonic device for each trig ratio starts with the first letter of the name of that ratio. For example, TOA starts with T, which stands for tan.
Next is the first letter of the side whose length is in the numerator of the trig ratio. Last is the first letter of the side whose length is in the denominator of the trig ratio. For example TOA means that the Opposite side is in the numerator of this trig ratio, and the Adjacent side is in the denominator.
SolutionIn order to determine the trig ratios, we need a right triangle. The pyramid can be cut in half by drawing a line from the peak to the center of the base. This gives us two right triangles. We can use one of these right triangles to determine trig ratios.
The mnemonic device for each trig ratio starts with the first letter of the name of that ratio. For example, SOH starts with S, which stands for $sin$.
Next is the first letter of the side whose length is in the numerator of the trig ratio. Last is the first letter of the side whose length is in the denominator of the trig ratio. For example SOH means that the Opposite side is in the numerator of this trig ratio, and the Hypotenuse is in the denominator. Or in other words:
$~$
$sin = \dfrac{\text{opposite}}{\text{hypotenuse}}$
$~$
Similarly, CAH means that:
$cos = \dfrac{\text{adjacent}}{\text{hypotenuse}}$
$~$
And TOA means that:
$tan = \dfrac{\text{opposite}}{\text{adjacent}}$
$~$
Let's identify the three side lengths that we need to calculate these ratios.
The opposite side to angle $A$ is $479.16$ ft long. This is the side that does not have the angle $A$ at either of its end points.
The adjacent side is the side between angle $A$ and the right angle. So its length is $377.50$ ft.
The hypotenuse is always the side that is opposite to the right angle. In this case it is $610$ ft long.
Now we can use the equations for the trig ratios, and the required side lengths, to calculate each ratio:
$~$
$sin = \dfrac{\text{opposite}}{\text{hypotenuse}}= \dfrac{479.16}{610}$
So we have that $sin = 0.786$.
$~$
$cos = \dfrac{\text{adjacent}}{\text{hypotenuse}}= \dfrac{377.50}{610}$
So we have that $cos = 0.619$.
$~$
$tan = \dfrac{\text{opposite}}{\text{adjacent}}= \dfrac{479.16}{377.50}$
So we have that $tan = 1.27$.
-
Find the missing length.
HintsRemember the mnemonic device "TOA".
The tangent ratio for an angle is equal to the length of the opposite side over the length of the adjacent side.
Once you calculate the length of the adjacent side using the tangent ratio, you will need to double it to get the full length of the base of the pyramid.
SolutionThe Pharaoh knows that for angle $A$, he has
$tan = 1.269$.
The height of the pyramid is opposite side to the angle $A$, and measures $20$ ft.
The mnemonic $TOA$ reminds him that $tan$ is equal to the opposite side over the adjacent side length:
$tan = \dfrac{\text{opposite}}{\text{adjacent}}$.
He can put in the known values and solve for the missing value:
$\begin{array}{rcl} 1.269 & = & \dfrac{20}{\text{adjacent}}\\ \color{#669900}{\times \, \text{adjacent} \, \div \, 1.269} & &\color{#669900}{\times \, \text{adjacent} \, \div \, 1.269}\\ \text{adjacent} & = & \dfrac{20}{1.269}\\ \text{adjacent} & = & 15.76 \end{array}$
He knows that the adjacent side length to angle $A$ in the right triangle is only half the length of the base of the pyramid. So he multiplies this adjacent side length by two to get the length of the base of the pyramid, $31.52$ ft.
-
Highlight the Pharaoh's mistakes.
HintsDon't assume that anything is correct, even the first equation.
When the Pharaoh is distracted, he sometimes flips the numerator and denominator in his equations.
The base is equal to two times the length of the side adjacent to angle $A$.
The Pharaoh should use the tangent ratio to start his calculations.
SolutionTo start with, we know the correct values of the three trig ratios for angle $A$, and we know the height of the desired pyramid. We want to find the length of one side of the base of the pyramid.
The Pharaoh's mistakes are noted below with an '✗' next to them. The rest is the correct solution to this problem.
We can find the base, $b$, as being equal to two times the adjacent side to angle $A$:
$b = 2 \times adj$.
The height of the pyramid is the opposite side to angle $A$. We have the length of the opposite side, and we need the length of the adjacent side. So we know that we need a trig ratio that includes both the opposite and adjacent sides. The tangent ratio meets this requirement:
$tan = \dfrac{\text{opp}}{\text{adj}}$.
✗ The Pharaoh wrote sin instead of $tan$.
We know that $tan A = 1.269$, and that the opposite side length is $12$. So:
$1.269 = \dfrac{12}{\text{adj}}$.
Using opposite operations:
$\begin{array}{rcl} 1.269 & = & \dfrac{12}{\text{adj}}\\ \color{#669900}{\div \, 1.269 \, \times \, \text{adj}} & &\color{#669900}{\div \, 1.269 \, \times \, \text{adj}}\\ \text{adj} & = & \dfrac{12}{1.269}\\ \text{adj} & = & 9.5 \end{array}$
✗ The Pharaoh switched the numerator and the denominator.
We know that $b = 2 \times adj$. Now we know the length of the adjacent side, so we can find the side length of the base $b$:
$b = 2 \times 9.5$, so
$b = 19$.
✗ The Pharaoh multiplied the adjacent side by 3, instead of two. As a result, he got the wrong side length for the base, even though he found the correct length of the side adjacent to angle $A$.
-
Determine the appropriate trig ratio.
HintsThe hypotenuse is always the side that is opposite the right angle. The opposite and adjacent sides are always relative to the target angle. Here, the hypotenuse is $5$ units long. The opposite side is $4$ units long, and the adjacent side is not labeled with a length.
Each triangle has two known side lengths. The sine, cosine, or tangent ratio will include both of the known side lengths.
SolutionFor each triangle we have a target angle and we know two side lengths. We must identify a trig ratio that can be found for the target angle using the known side lengths.
Let's start by identifying which side lengths we know, with respect to the target angle.
For the first pendant, the side with a length of $4$ units is opposite angle $b$. We can verify this by observing that angle $b$ is not at either end point of this side. Similarly, the side with a length of $5$ is the hypotenuse because it is opposite the right angle.
Sin is the trig ratio that includes the opposite side, and the hypotenuse. So we should use sin to characterize angle $b$ in the first pendant.
For the second pendant, we have an hourglass shape. The top half of the hourglass is a right triangle. Angle $b$ is the target angle. The side with a length of $2$ units is the adjacent side to angle $b$, because is goes between angle $b$ and the right angle. The side with a length of $3$ units is the hypotenuse because it is opposite the right angle. The cos trig ratio includes both the adjacent side and the hypotenuse, so we should use this ratio for angle $b$ in this triangle.
For the third pendant, the side with a length of $4$ units is adjacent side because it is between angle $b$ and the right angle. The side with a length of two is opposite to angle $b$; $tan$ is the trig ratio that includes both the opposite and the adjacent sides.
For the fourth pendant, we have a rectangle that is split to form two right triangles. Looking at angle a in the upper triangle, the side with a length of $3$ units is the adjacent side because it is between angle $b$ and the right angle. The side with a length of $4$ units is the hypotenuse because it is opposite the right angle.
-
Identify the sides.
HintsRemember that the Pharaoh's name, SOHCAHTOA, can help you remember the trig ratios.
The Pharaoh's name breaks into three syllables, each of which helps you remember one of the trig ratios. The three letters stand for the trig ratio, and the sides that belong in the numerator and denominator of that ratio.
SolutionThe mnemonic device SOHCAHTOA breaks into three parts, one for each of the trig ratios. They are SOH, CAH, and TOA. Each starts with the first letter of the name of that ratio. For example, SOH starts with S, which stands for $sin$.
The next letter stands for the side whose length is in the numerator of the trig ratio. The last letter stands for the side whose length is in the denominator of the trig ratio. For example SOH means that the opposite side is in the numerator of this trig ratio, and that the hypotenuse is in the denominator. In other words:
$~$
$sin = \dfrac{\text{opposite}}{\text{adjacent}}$
$~$
Similarly, CAH means that:
$cos = \dfrac{\text{adjacent}}{\text{hypotenuse}}$
$~$
And TOA means that:
$tan = \dfrac{\text{adjacent}}{\text{opppsite}}$
$~$
The opposite side to angle $A$ is the side that does not have the angle $A$ at either of its end points.
The adjacent side is the side between angle $A$ and the right angle.
The hypotenuse is always the side that is opposite to the right angle.
-
Complete the trig ratios.
HintsRemember that the opposite and adjacent sides are named with respect to the target angle. So the opposite side for angle $B$ is different than the opposite side for angle $A$.
It may help to write out the equations in numbers and symbols, in order to understand how to fill in the blanks in the sentences.
Remember, the Pharaoh's name, SOH-CAH-TOA, can help you remember what sides are in the numerator and the denominator of each trig ratio.
SolutionRecall the trig ratios:
$sin = \dfrac{\text{opp}}{\text{hyp}}$
$cos = \dfrac{\text{adj}}{\text{hyp}}$
$tan = \dfrac{\text{opp}}{\text{adj}}$
For the first triangle, the hypotenuse is 206 ft long, and does not change depending on the angle. For angle $A$, the opposite side is 100 ft long because this is the side that does not have angle $A$ at either of its end points. The adjacent side is 180 ft long because this is the side that goes between angle $A$ and the right angle. For angle $B$, the opposite side is 180 ft long, and the adjacent side is 100 ft long.
So we can find cosine ratio as:
$cos \, A = \dfrac{180}{206}$
$cos \, A = 0.874$
So the cosine of angle A is equal to 180 divided by 206. The ratio is 0.874.
Similarly:
$tan \, B = \dfrac{180}{100}$
$tan \, B = 1.8$
$sin \, A = \dfrac{100}{206}$
$sin \, A = 0.485$
And for the second triangle:
$sin \, A = \dfrac{40}{50}$
$sin \, A = 0.8$
$tan \, B = \dfrac{30}{40}$
$tan \, B = 0.75$












Omg, I almost died of second hand embarrassment!!
lol
That cat pun counter really worried me with the amount of numbers available!