Calculations with Supplementary, Complementary, and Vertical Angles

Basics on the topic Calculations with Supplementary, Complementary, and Vertical Angles
After this lesson you will be able to use definitions of special angles to solve for unknown angles.
The lesson begins by defining and identifying right, complementary, supplementary, and vertical angles. It leads to finding the measurements of angles given two measurements. It concludes with solving for angle measurements by using angle relationships to set up equations.
Learn about angles by helping Pete create the perfect pizza slices for his customers at Pete’s Pizza Paradise!
This video includes key concepts, notation, and vocabulary such as: adjacent angles (two angles who share a “side” (a ray) and a vertex); supplementary angles (two angles that sum to 180 degrees); complementary angles (two angles that sum to 90 degrees); vertical angles (“opposite” angles with equal measures that are formed by two intersecting); Vertical Angle Theorem (Vertical angles are congruent).
Before watching this video, you should already be familiar with the terms: adjacent, supplementary angles, complementary angles, vertical angles, and the relationships between them.
After watching this video, you will be prepared to learn about angle relationships when parallel lines are cut by a transversal.
Common Core Standard(s) in focus: 7.G.B.5 A video intended for math students in the 7th grade Recommended for students who are 12-13 years old
Transcript Calculations with Supplementary, Complementary, and Vertical Angles
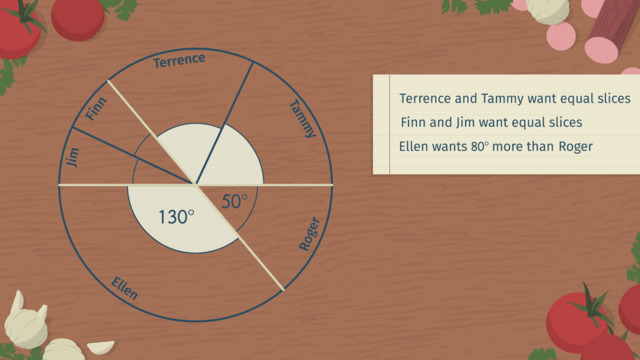
Pete's Pizza Paradise is really taking off, and it's not just because of his mouth-watering tomato sauce and crispy thin crust! They also love that they can customize the way the pizza is sliced! To meet his customers' demands, Pete has become an expert at calculations involving supplementary, complementary, and vertical angles. When ordering a whole pizza from Pete, the customer just has to draw out their preferred slicing and Pete takes care of the rest. Let's take a closer look at Pete's first order of the day. They want the pizza divided into 5 slices. Can you identify a right angle in the diagram? Angle 1 is a right angle. Now what can we say about angles 2 and 3? They aren't equal, but what happens when we add them together? 40 degrees plus 50 degrees is 90 degrees. That means 2 and 3 are complementary angles. Remember, any two angles that add up to 90 degrees are called complementary angles. And when adjacent, they form a right angle. How about angles 3 and 4? 40 plus 140 is 180 degrees so 3 and 4 are supplementary angles. We can see that visually too: they are angles on a line! How about angle 3 and angle 5? They are formed by the intersection of two lines... and they are not adjacent to each other. Three and five are vertical angles which means they have to have the same measure. The pizza emerges from the oven bubbling and delicious! Pete slices it like a pro, beginning with a straight angle. I wonder which lucky luncher gets the 140 degree slice? Here comes another order, but it's a bit incomplete! Only two specific angles are given! But is that information enough to find out the measures of all the other slices? Let's label these three unknown angles 'a,', 'b' and 'c'. Now it's time to start calculating and see how far we get. Can you see two supplementary angles? These two angles are supplementary because they are angles on a line. That means, thirty degrees plus 'a' degrees equals 180 degrees. Subtracting gives us 'a' equals 150 degrees. Can you see two vertical angles? These two angles are vertical, which means they have equal measures. So we can write 'b' plus 20 degrees is equal to 30 degrees. Subtracting gives us 'b' equals 10 degrees. What a tiny slice! Can you see a right angle in the diagram? This angle is a right angle, which means its measure is 90 degrees. This half-circle represents a straight angle of 180 degrees. So 10 plus 90 plus 'c' equals 180 degrees. A hundred plus 'c' equals 180 which gives us 'c' equals 80 degrees. Pete slices up the pizza. His only question is, who's going to be stuck with that 10 degree slice? The orders keep on flying in! How can Pete keep up?!? Hm, this order looks a bit strange: they just drew some slices, added their names, and gave some instructions. We know that Terrence and Tammy want equal slices, but we don't know their sum. Finn and Jim also want equal slices, but we don't know their sum. Finally, Ellen wants 80 degrees more than Roger. Which of these three statements might give us an equation we can solve? Ellen's slice will be 80 degrees more than Roger's. Can you see a relationship between Ellen's slice and Roger's slice? These two angles are supplementary, which means we can write and solve an equation. Let's call the measure of Roger's slice 'x'. That means the measure of Ellen's slice is 'x' plus 80 degrees. Since these two angles are supplementary, 'x', plus 'x' plus 80 degrees equals 180 degrees. That's 2 'x' plus 80 equals 180. Two 'x' equals 100, and so, 'x' equals 50 degrees. Roger's slice is 50 degrees and Ellen's slice is 50 plus 80, which equals 130 degrees! Ellen's slice is vertical to Terrence and Tammy's combined so Terrence and Tammy's slices together measure 130 degrees. Since they are equal, each measures half of 130 which is 65 degrees. Roger's slice is vertical to Finn's and Jim's combined. So Finn and Jim's slices together measure 50 degrees, which means each measures 25 degrees. Pete slices the pizza to perfection. But he wonders, how will Ellen ever properly fold and eat such a giant slice? While the happy customers are enjoying their pizza pies let's review some tasty techniques for problem solving with angle pairs. First, identify supplementary complementary and vertical angles. Combine this with your given information to decide where to assign variables. Write and solve equations to solve for unknowns. Then slice your pizza to order! I'm a bit worried about Pete. He seems completely overworked! Oh, he looks a lot better from a more complementary angle. Pete's passion for pizza is the perfect supplement to his pleasant personality!











YASSSSSSSSSSS
💅🏾💅🏾👌🏾👌🏾