Using the Law of Sines and Cosines to Find Angles


Basics on the topic Using the Law of Sines and Cosines to Find Angles
For any non-right triangle, if two sides together with the angle opposite to one of them are known, then you can use the law of sines to compute the angle opposite to the other known side.
For a given triangle with side lengths a, b, and c, the law of sines states that
a b c --------- = --------- = ---------, sin A sin B sin C
where A, B, and C are the angles opposite to a, b, and c, respectively. You just need to make use of the relevant pair of ratios and remember that, when working with proportions, the product of the means equals the product of the extremes.
If only all three sides lengths are given, and you need to look for an angle, then you can use the law of cosines.
For a given triangle with side lengths a, b, and c, the law of cosines states that
c2 = a2 + b2 – 2ab(cosC) b2 = a2 + c2 – 2ac(cosB) a2 = b2 + c2 – 2bc(cosA)
where A, B, and C are the angles opposite to a, b, and c, respectively.
Apply trigonometry to general triangles.
CCSS.MATH.CONTENT.HSG.SRT.D.11
Transcript Using the Law of Sines and Cosines to Find Angles
Pete manages lighthouses on three islands: Aurora's Alluvia, Bruce's Bluff and Clark's Cliff. Pete, the lighthouse keeper, notices that one of the three lighthouses he manages has just gone out. Pete must act quickly before disaster strikes, but it's slow going because the fog is as thick as split pea soup. How will he find the lighthouse in all this fog? No worries. Pete can use the Law of Sines and Cosines to Solve for Unknown Angles.
Law of Cosines
To calculate the angle of a non-right triangle when you know all the sides, or just two sides and one angle, you can use the Law of Cosines. Since Pete knows the distances between the three lighthouses. He just needs to figure out the unknown angle, and then set the course of his boat.
Let’s review the formulas. To make these formulas easier to memorize, notice the pattern - it's similar to the Pythagorean Theorem with some extras. Let's take a look. Does the first part of the equation look familiar? It should it's the Pythagorean Theorem! Notice a pattern? That's right. All we have to do to get the Law of Cosines is subtract the product of the cosine of the angle opposite the side you're trying to find and 2 times the product of the remaining sides from our original Pythagorean Theorem.
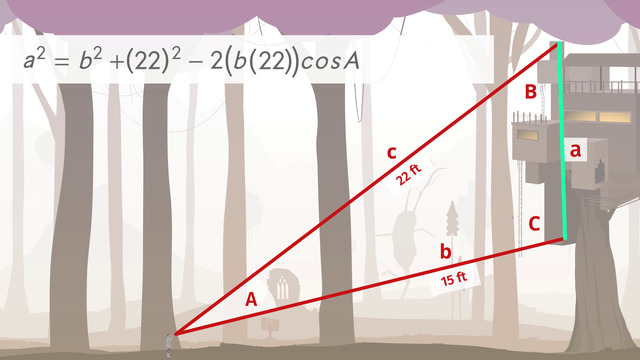
But which formula should we use? Since the unknown quantity is ∠A, we can use this formula, but first, let's modify it to solve for cos(A). Oh boy, that looks really complicated - we may need a calculator for this. Let’s try it out. Pete already knows that the distance between Bruce's Bluff and Clark's Cliff is equal to 5.18 miles, between Aurora's Alluvia and Clark's Cliff is 9 miles and the distance between Aurora's Alluvia and Bruce's Bluff is 6 miles. Pete plugs in the known distances into the Law of Cosines formula. Ok now that Pete knows the angle he can set off for Clark's Cliff.
Oh no… the replacement bulb is overboard! To get a replacement bulb he'll have to go to Bruce's Bluff. But now he'll need to chart a course to get from Bruce's Bluff to Clark's Cliff.
Law of Sines
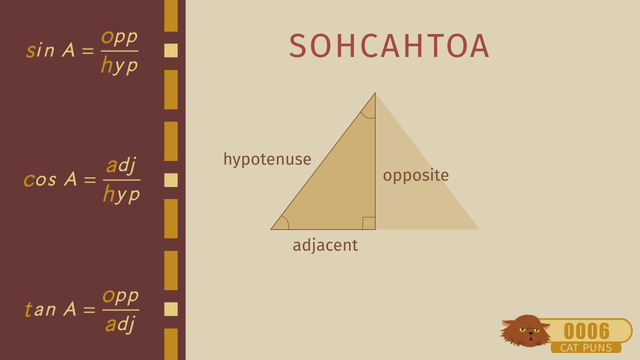
He can calculate the cosine of angle B, but since he knows at least two sides and one of the opposite angles now, he can use the Law of Sines. Take a look at the formula for the Law of Sines. The lower case letters indicate the length of the three sides, and the upper case letters indicate the measure of the angles opposite the respective sides. Look! You can also turn the formula upside down. Use the formula that's easiest for you to remember to solve for the unknown measurement.
Okay, let’s use what we know to solve for angle B. Since Pete knows the distances to and from each of the islands as well as the degree measure between AB and AC, he can use the Law of Sines to find the direction of Clark's Cliff. Pete plugs in the known distances, this time, into the Law of Sines formula. Ok...Pete's all set to fix the light bulb.
But through the fog, he gets distracted by a mermaid? Pete decides a LITTLE detour might not be the worst thing. Oops, that’s not a mermaid…
Using the Law of Sines and Cosines to Find Angles exercise
-
Calculate the angle using the law of sines.
HintsYou can use opposite operations to solve this equation.
Start by substituting in the given values.
Not all given values will be needed.
SolutionStart with the given equation from the law of sines:
$\dfrac{a}{\sin A}=\dfrac{b}{\sin B}$.
Substitute in the given values:
$\dfrac{5.18}{\sin 33.4°}=\dfrac{9}{\sin B}$.
Use opposite operations to begin to isolate B:
$5.18(\sin B)=9(\sin 33.4°)$
$\sin B=\dfrac{9(\sin 33.4°)}{5.18}$.
Apply the inverse $\sin$ to both sides,
$B=\sin^{-1}(\dfrac{9(\sin 33.4°)}{5.18})$,
to get $B=73°$.
-
Find angle $A$ using the law of cosines.
HintsThe angle $A$ is written with a capital $A$, while the side $a$ is written with a lowercase $a$.
Before isolating $A$ completely, Pete needs to isolate $\cos A$.
To convert $\cos A$ into $A$, Pete should apply the inverse cosine operation.
SolutionThe law of cosines states that:
$a^2 = b^2 + c^2 - 2(bc)\cos A$
$b^2 = a^2 + c^2 - 2(ac)\cos B$
$c^2 = a^2 + b^2 - 2(ab)\cos C$
The first equation is the only one that includes the angle $A$, so this is the equation Pete must use.
Pete must use opposite operations to isolate $\cos A$:
$b^2 + c^2 - a^2 = 2(bc)\cos A$
$\dfrac{b^2 + c^2 - a^2}{2(bc)} = \cos A$
Next he must apply the inverse cosine operation to both sides. This will completely isolate $A$ on the right hand side.
$\cos^{-1}(\dfrac{b^2 + c^2 - a^2}{2(bc)}) = A$
Substituting in known values, Pete finds:
$\cos^{-1}(\dfrac{9^2 + 6^2 - 5.18^2}{2(9)(6)}) = A$
$A = 33.4°$
-
Determine the law of cosines equation.
HintsIt will help to begin by writing down the law of cosines equation that includes angle $A$, and then to rearrange this equation to isolate $A$.
It may help you to assign the labels $a$, $b$, and $c$ to the side lengths of each triangle.
SolutionWe must find an equation that shows the angle $A$ in terms of the side lengths. We can do this using the law of cosines, which states that:
$a^2 = b^2 + c^2 - 2(bc)\cos A$
$b^2 = a^2 + c^2 - 2(ac)\cos B$
$c^2 = a^2 + b^2 - 2(ab)\cos C$
In each case we are looking for angle $A$. The first equation is the only one that includes the angle $A$, so this is the equation that we must use.
We must first isolate $\cos A$. We can do this using opposite operations:
$b^2 + c^2 - a^2 = 2(bc)\cos A$
$\dfrac{b^2 + c^2 - a^2}{2(bc)} = \cos A$
Next he must apply the inverse cosine operation to both sides. This will completely isolate $A$ on the right hand side.
$\cos^{-1}(\dfrac{b^2 + c^2 - a^2}{2(bc)}) = A$.
Now we can substitute our known values for each triangle into this equation.
Recall that the side length $a$, is the side opposite angle $A$. Therefore for the first triangle:
$a = 5.18$
$b = 9$
$c = 6$
Substituting these values into the equation we found above yields:
$cos^{-1}(\dfrac{9^2 + 6^2 - 5.18^2}{2(9)(6)}) = A$.
Similarly, for the second triangle:
$a = 7$
$b = 9$
$c = 8$
$cos^{-1}(\dfrac{9^2 + 8^2 - 7^2}{2(9)(8)}) = A$.
For the third triangle:
$a = 2$
$b = 3$
$c = 4$
$cos^{-1}(\dfrac{3^2 + 4^2 - 2^2}{2(3)(4)}) = A$.
For the fourth triangle:
$a = 7$
$b = 8$
$c = 9$
$cos^{-1}(\dfrac{8^2 + 9^2 - 7^2}{2(8)(9)}) = A$.
-
Solve for the angle Pete needs to navigate to the island.
HintsThink about how you can use the law of cosines to find the missing angle.
Since the points on this triangle are $A$, $C$, and $D$, it may help to substitute these variable names into the law of cosines equation.
Remember that the side length is named by the angle it is opposite to. For example, side $a$ is opposite angle $A$.
SolutionPete must find angle $A$, given all side lengths of a triangle.
The law of cosines states that:
$a^2 = b^2 + c^2 - 2(bc)\cos A$
$b^2 = a^2 + c^2 - 2(ac)\cos B$
$c^2 = a^2 + b^2 - 2(ab)\cos C$
The first equation is the only one that includes the angle $A$, so this is the equation that Pete must use.
Pete's triangle has points $A$, $C$, and $D$, so he decides to substitute $d$ in for $b$ in the equation:
$a^2 = d^2 + c^2 - 2(dc)\cos A$
Pete must use opposite operations to isolate $\cos A$:
$d^2 + c^2 - a^2 = 2(dc)\cos A$
$\dfrac{d^2 + c^2 - a^2}{2(dc)} = \cos A$
Next he must apply the inverse cosine operation to both sides. This will completely isolate $A$ on the right hand side.
$cos^{-1}(\dfrac{d^2 + c^2 - a^2}{2(dc)}) = A$
Pete knows that the side a is opposite angle $A$ in a triangle. He determines the side lengths of this triangle to be:
$a = 4$
$d = 9$
$c = 6.5$
Substituting in known values, Pete finds that
$cos^{-1}(\dfrac{9^2 + 6.5^2 - 4^2}{2(9)(6.5)}) = A$.
So $A = 30.3°$.
-
Define the law of cosines.
HintsPay close attention to the signs.
Only one of the equations is correct.
It may help to write out the equations of the law of cosines, and then compare these equations to the ones given.
SolutionThe equations given by the law of cosines are:
- $a^2 = b^2 + c^2 - 2(bc)\cos A$
- $b^2 = a^2 + c^2 - 2(ac)\cos B$
- $c^2 = a^2 + b^2 - 2(ab)\cos C$
✓ $a^2 = b^2 + c^2 - 2(bc)\cos A$
This equation matches equation $1$ exactly.
✗ $b^2 = a^2 - c^2 - 2(ac)\cos B$
This equation almost matches equation $2$, but the sign on the $c^2$ term is wrong.
✗ $c^2 = a^2 + b^2 + 2(ab)\cos C$
This equation almost matches equation $3$, but the sign on the $2(ab)\cos C$ term is wrong.
✗ $a^2 = b^2 + c^2 - 2(ac)\cos A$
This equation almost matches equation $1$, but the term multiplied by $\cos a$ should be $-2(bc)$ instead of $-2(ac)$.
-
Identify the values of the angles marking potential new locations for lighthouses.
HintsLook at the equations given by the law of sines and law of cosines. Which equations contain the unknown value, and only other known values?
Be careful with signs as you use opposite operations to isolate the required variable.
SolutionPete determines that to find angle $B$, he should use the law of cosines, which includes one angle and all side lengths of a triangle. Pete knows that the three equations given by the law of cosines are:
- $a^2 = b^2 + c^2 - 2(bc)\cos A$
- $b^2 = a^2 + c^2 - 2(ac)\cos B$
- $c^2 = a^2 + b^2 - 2(ab)\cos C$
He must determine $B$ for the first triangle, so he can see that he must use equation $2$, which is the only one that includes the angle $B$.
He isolates $B$ in the equation using opposite operations:
$b^2 = a^2 + c^2 - 2(ac)\cos B$
$2(ac)\cos B = a^2 + c^2 - b^2$
$\cos B = \dfrac{a^2 + c^2 - b^2}{2(ac)}$
He finishes isolating $B$ by applying $\cos^{-1}$ to both sides:
$B = \cos^{-1}(\dfrac{a^2 + c^2 - b^2}{2(ac)})$
He knows that the side lengths for the first triangle are:
$a = 11$
$b = 12$
$c = 8$
Substituting in these values, he gets:
$B = \cos^{-1}(\dfrac{11^2 + 8^2 - 12^2}{2(11)(8)})$
He finds angle $B$ to be $76.5°$.
Similarly, for the second triangle, he uses equation $3$, and finds angle $C$ to be $27.7°$.
For the second triangle, he uses equation $1$, and finds angle $A$ to be $112.6°$.