Trigonometry
Easy learning with videos, exercises, tasks, and worksheets
Most popular videos
Content
What is Trigonometry?
Just the word trigonometry makes you think of triangles. Trigonometry is the study of the measure of the angles and sides of triangles.
Triangle Review
Triangles come in different shapes and sizes, but they all have one thing in common, their three interior angles sum to 180 degrees. Also, the sum of two side lengths of a triangle must be greater than the length of the third side.
The first example is an equilateral triangle, where all interior angles are 60 degrees:
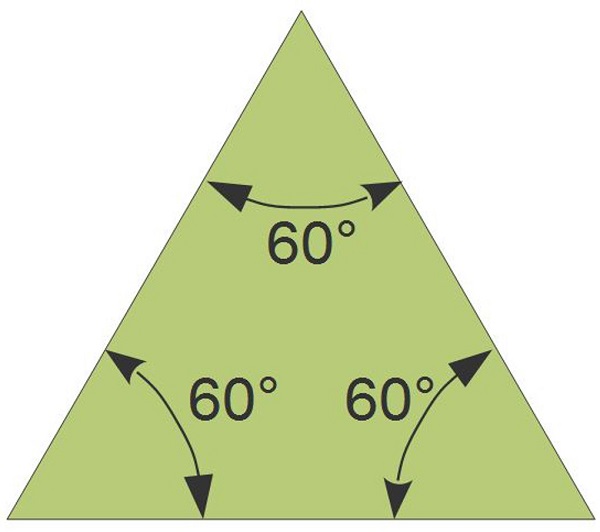
Next is an image of an isosceles triangle, which has two angles of the same degree:
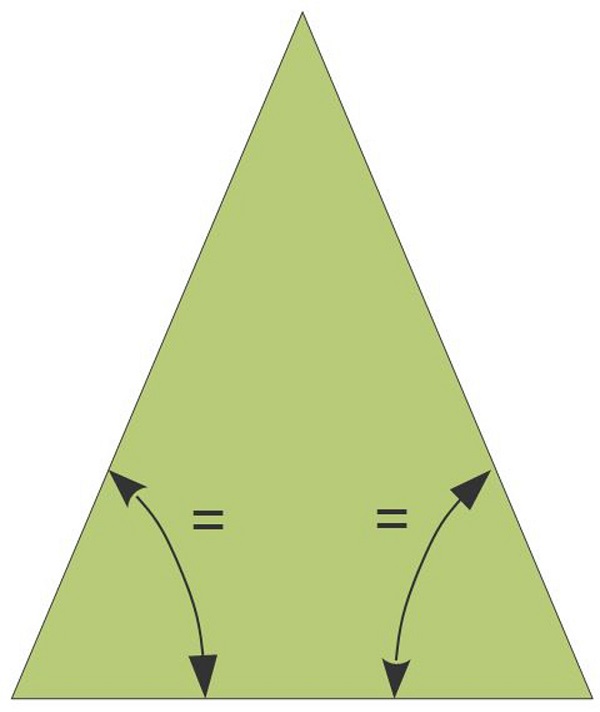
Here you can see a scalene triangle, where all sides have different lengths and all angles are different:
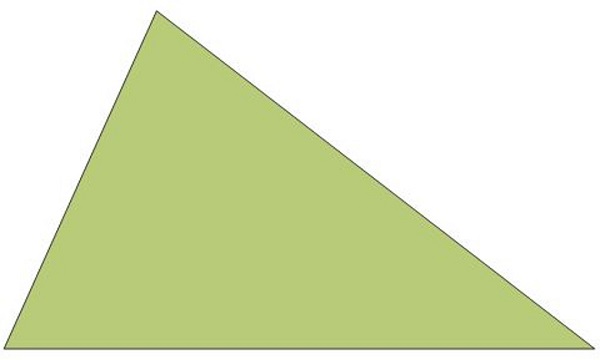
The last example image shows a right triangle, which has one interior angle of 90 degrees:
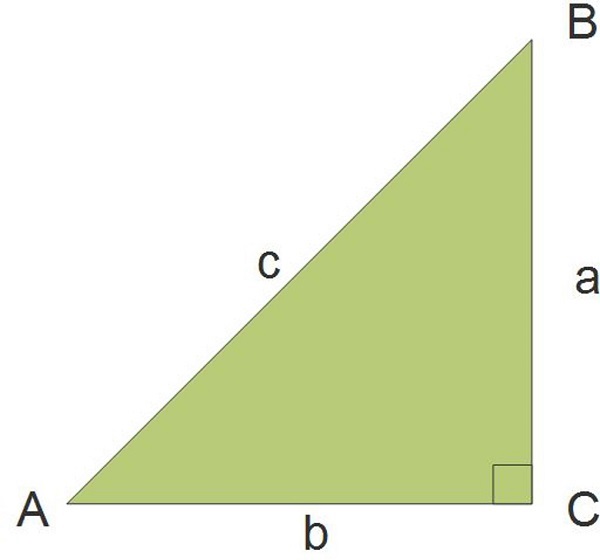
Pythagorean Theorem
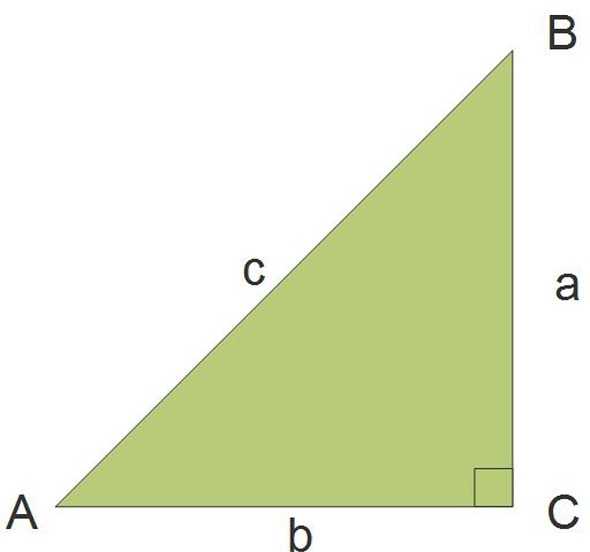
More than 2,000 years ago, Greek mathematician Pythagoras made a discovery about the relationship of the sides of right triangles. Today, we know this discovery as the Pythagorean Theorem. For all right triangles, with the hypotenuse as side c, the Pythagorean Theorem states:
$a^{2} + b^{2} = c^{2}$
Trigonometric Ratios in Right Triangles
For all right triangles, there is also a special relationship between the three sides and the three angles. The relationship between a triangle’s sides and angles is the basis of trigonometric ratios.
Finding Trigonometric Ratios
To study the trig ratios, you need to know how the appropriated terminology to describe the sides and their related angles.

The hypotenuse is located opposite the right angle. For angle A, the side across from the angle is the opposite side, and the side next to the angle, but not the hypotenuse, is the adjacent side.
The basic trig ratios are sine, cosine, and tangent. An easy mnemonic device to remember the trigonometric ratios is SOHCAHTOA:

Using Trigonometric Ratios to Find Angles
To find unknown angles, use the trig ratios to set up an equation then solve for the unknown value.
To use the sine ratio to solve for the unknown angle, use the trig chart or use a calculator to find the inverse of sine x.
Example: Find the measure of angle x.

$\begin{align} \sin x &= \frac{opp}{hyp}\\ \sin x &= \frac{6}{10}\\ \sin x &= 0.6\\ x &= \frac{0.6}{sin}\\ x &= 36.869 \end{align}$
x is approximately 37 degrees
Using Trigonometric Ratios to Find Distances
To find unknown sides, use the trig ratios to set up an equation then solve.
To use the sine ratio to solve for the unknown side, use the trig chart or a calculator.
Example: Find the length of side x.
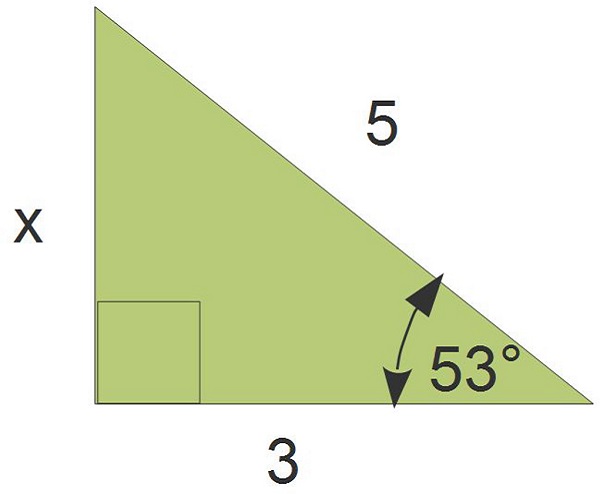
$\begin{align} \sin 53 &= \frac{x}{5}\\ 0.8&=\frac{x}{5}\\ 0.8 \times 5&=\frac{x}{5}\times 5\\ x&=4.0 \end{align}$
The length of the unknown side is 4 units.
Special Triangles
There are two special triangles, 45-45-90 and 30-60-90. What’s special about these two triangles? The angles and side lengths of the two special triangles have a special pattern that holds for any size triangle with the same angles.

All videos on the topic
Videos on the topic
Trigonometry (7 videos)
All worksheets on the topic
Worksheets on the topic
Trigonometry (6 worksheets)










 Trig Ratios in Right Triangles
Trig Ratios in Right Triangles
 The Pythagorean Theorem
The Pythagorean Theorem
 Using the Law of Sines and Cosines to Find Angles
Using the Law of Sines and Cosines to Find Angles
 Using Trig. Ratios to Find Distances
Using Trig. Ratios to Find Distances
 Triangle Review
Triangle Review
 Special Triangles
Special Triangles









