Zero and Negative Exponents
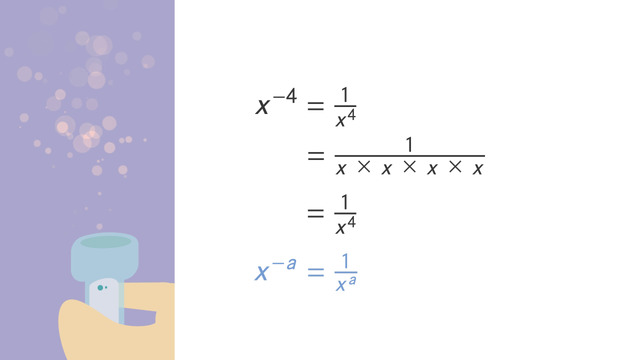
Basics on the topic Zero and Negative Exponents
Summary of Zero and Negativ Exponents
Negative Exponents may seem confusing but if you know the properties of exponents, solving problems will be much easier to understand, and the strategies to solve the problems will be much easier to remember.
First let’s review the Property of Zero Exponents. The property states that any base raised to the zero power is equal to one – that’s any base. So one million raised to the zero power is equal to one? That’s right.
How will this help us to understand negative exponents? Let’s consider a fraction: The numerator is equal to 7 raised to the zero power, and the denominator is equal to 7 raised to the second power. If we simplify this we get a fraction with 1 as the numerator and 49 as the denominator:
To make this concept easier to understand, use the Quotient of Powers Property. For same bases in the numerator and denominator, simply subtract the exponents, so for this same fraction, we can subtract 2 from 0 to calculate the difference of -2. So 7 raised to the -2 power is equal to Now, this makes sense and since it makes sense, it’s so much easier to remember how to solve problems with negative exponents. Just remember, for a negative exponent, write a 1 in the numerator, and in the denominator, write the base raised to the absolute value of the negative exponent.
To have a laugh and watch some examples of zero and negative exponents, get a bowl or popcorn and watch this video.
Interpret the structure of expressions.
Common Core
CCSS.MATH.CONTENT.HSA.SSE.A.1
Let's practice: zero and negative exponents Exercises
With the following exercises on the topic of zero and negative exponents, you can test whether you have understood everything. Test your knowledge now!
Transcript Zero and Negative Exponents
In a land of two kingdoms, rival Kings Wallace the 4th and Frederick the negative 3rd enjoy playing pranks on each other. King Wallace receives a package from his rival, but is it a package or a prank ? It’s a painting…
Oh my! How provocative! In order to maintain diplomatic relations , the king must hang the painting in a prominent position...this is a terribly tricky situation, so the king calls Mr. Magic, the court mathemagician. Mr. Magic knows just what to do. He’ll shrink the painting From his bag of tricks, he pulls out a secret potion...and leaves the rest to magic.
The fraction
Oh no! The shrinking potion only worked in one dimension – look what happened. Mr. Magic realizes his error ...so he pulls out another potion - this time to shrink the provocative painting proportionally by 10⁻⁵. 10⁻⁵! Wait – negative powers can be confusing. Let’s investigate. Take a look at our problem here, 10⁻⁵. We can rewrite this as a fraction. In the denominator, write the base to the absolute value of the power, or 10⁵. So, what do you write in the numerator? 1.
Denominator and numerator
Now, simplify the fraction. See what happens when you have a positive exponent in the denominator of a fraction? The value of the fraction get smaller and smaller. 10⁻⁵ = 1/100,000. I think Mr. Magic is on to something here…Take a look at this example: 2⁻⁴. To rewrite this as a fraction, in the denominator, write 2⁴, then, write a one in the numerator, and simplify. 2⁻⁴ = 1/16.
Example
Let's look at an example when the base is a variable. We can rewrite x⁻⁴ as a fraction by writing x⁴, which is x times x times x times x in the denominator and a 1 in the numerator. This simplifies to 1/x⁴. Here's the rule for negative exponents: x⁻ª = 1/xª. Remember, 'x' cannot be equal to zero. Let's look at a rule to see why this works, and then it will be easier to remember…
The rule
Our rule is: any base raised to the zero power is equal to 1, for example, 1⁰ = 1...2⁰ = 1, and 3⁰ = 1, and so on...the rule is: any base, such as x, raised to the zero power is equal to 1, when 'x' does not equal 0.
So, using the example, 2⁻⁴, rewritten as a fraction, is equal to 1/2⁴ is the same as 2⁰ over 2⁴ and like magic, this is equal to 2⁽⁰⁻⁴⁾, which is 2⁻⁴, so we're right back where we started. That makes it much easier to understand! Sometimes math is like magic!
King Wallace hung the picture. But wait, where is it? Ah, there. Take a look at it now… Thanks to Mr. Magic, King Wallace isn’t worrying about the picture – he’s trying to figure out what prank to play next on King Frederick…
Zero and Negative Exponents exercise
-
Decide what $10^{-5}$ stands for.
HintsFor example, $10^3=10\times 10\times 10$.
You multiply two decimal powers by adding their exponents:
$10^7\times 10^{-5}=10^{7-5}=10^2$.
Here you see how to handle a negative exponent for $x\neq 0$.
SolutionMr. Magic shrinks the picture by a decimal power: $10^{-5}$. How can we see what this negative decimal power is trying to express? Using what we know about multiplying and dividing powers with exponents, we can see that:
$10^{\large -5}=10^{\large 0-5}=10^{\large 0}\div 10^{\large 5}=1\div 10^{\large 5}=\frac{1}{10^{\large 5}}=\frac{1}{100000}$.
-
Explain why $2^{-4} = \frac1{2^4}$ is true.
HintsHere is the rule for dividing powers with the same basis.
Each power with a zero exponent is equal to $1$ for $x\neq 0$:
$\large x^0=1$
SolutionWe start with the fraction $\frac1{2^{\large 4}}$.
Since each power with a zero exponent is equal to $1$, we have that $2^{0}=1$. So $1$ over $2$ to the power of $4$ is equal to $2^{0}\div 2^{4}$.
Since $2^{4}$ and $2^{0}$ have the same basis, we can subtract their exponents by the rule for dividing powers to get $2^{0-4}$.
We then have that $\frac1{2^{\large 4}}=2^{-4}$.
-
Examine the following powers with negative exponents.
HintsKeep the general formula for negative exponents in mind.
Count the number of zeros in the denominator.
The number of zeros in the denominator is the same as the absolute value of the exponent.
SolutionIn general we have $x^{-a}=\frac1{x^{\large a}}$, where $x\neq 0$.
So if we have $x=10$, we get:
- $10^{-3}$$=\frac1{10^{\large 3}}=\frac1{1000}$
- $10^{-1}$$=\frac1{10^{\large 1}}=\frac1{10}$
- $10^{-6}$$=\frac1{10^{\large 6}}=\frac1{1000000}$
- $10^{-7}$$=\frac1{10^{\large 7}}=\frac1{10000000}$
-
Decide the power of the enlarging potion.
HintsFind the shrinking factor of the spell.
Divide the size of the shrunken castle by the size of the original castle.
The enlarging factor is the reciprocal of the shrinking factor.
If you write the shrinking factor as $1$ over a decimal power with a positive exponent, you can find the reciprocal directly.
SolutionFirst let's find the shrinking factor of the spell. To do this, we divide the resulting size of the castle $2$ by the original size $200$:
$\frac2{200}=\frac1{100}=\frac1{10^{\large 2}}$.
Writing this as a decimal power with a negative exponent we get $10^{-2}$.
So to undo the shrinking, we have to multiply by $10^2=100$.
Let's check: $2\times 100=200$ $\surd$.
So $10^2=100$ is the enlarging factor we need for the potion.
-
Explain how to write $x^{-a}$ as a fraction.
HintsAn example of a negative exponent is $2^{-4}=\frac1{2^{\large 4}}$.
An example with $x$ as the basis is $x^{-4}=\frac1{x^{\large 4}}$.
Remember that division by zero isn't allowed.
SolutionWe've already seen that
$10^{-5}=\frac1{10^{\large 5}}$
We can prove that $2^{-4}=\frac1{2^{\large 4}}$ using $2^0=1$:
$\begin{array}{lcr} \frac1{2^{\large 4}}&=&\frac{2^{\large 0}}{2^{\large 4}}\\ &=&2^{0-4}\\ &=&2^{-4} \end{array}$
Similarly we have $x^{-4}=\frac1{x^{\large 4}}$.
In general, we have
$x^{-a}=\frac1{x^{\large a}}$.
As long as the basis does not equal zero, if we have a power with a negative exponent we can also write it as a fraction with $1$ in the numerator and the power with the same basis to the absolute value of the exponent in the denominator.
-
Identify the powers resulting from the calculations shown.
HintsIn general $\large 10^{-a}=\frac1{10... 0}$, where the number of zeros in the denominator is the same as the absolute value of the exponent.
If you divide $1$ by a decimal power you get the resulting decimal number, $0.0...01$, where the position of $1$ after the comma is the same as the exponent.
SolutionLet's start with the fraction $\frac{10^{\large 3}}{10^{\large 6}}$.
Since we have two powers with the same basis, we can subtract the exponents to get $\frac{10^{\large 3}}{10^{\large 6}}=10^{\large 3-6}=10^{\large -3}$.
Next we can write the power as a fraction $10^{\large -3}=\frac1{1000}$. To get the corresponding decimal number we write the $1$ in the third position after the comma:
$\frac{10^{\large 3}}{10^{\large 6}}=\frac1{1000}=0.001$.
$~$
Next we multiply two powers with the same exponents: $\left(\frac12\right)^{\large -4}\times 20^{\large -4}$. First we multiply both base numbers together to get $\frac12\times 20=10$.
The resulting power has the same exponent as both factors. So we have $\left(\frac12\right)^{\large -4}\times 20^{\large -4}=10^{\large -4}$.
Again we write this power as a fraction and after as a decimal number: $10^{\large -4}=\frac1{10^{\large 4}}=\frac1{10000}=0.0001$
$~$
We handle the last, $8^{\large -3}\times125^{\large -3}$, in a similar manner.
We have $8\times 125=1000=10^{\large 3}$, so we can conclude that $8^{\large -3}\times125^{\large -3}=\left(10^3\right)^{-3}=10^{\large -9}$.
Writing this result as a fraction and a decimal number, we get $10^{\large -9}=\frac1{10^{\large 9}}=\frac1{1000000000}=0.000000001$.