Surface Area - combined straight edge objects

Basics on the topic Surface Area - combined straight edge objects
The sum of the areas of the faces of a 3D shape is called its surface area. A knowledge of getting the area of faces of 3D shapes is very useful in areas where spatial awareness is important like architecture, engineering, science, arts, games, and in many aspects of everyday life. A proficiency in calculating the surface area plays a major role in chemical kinetics since there is a direct relationship between the surface area of the reactants and the rate of a chemical reaction. Learn how to calculate the surface area of some 3D shapes by helping Calvin, who’s home alone for the day, set up a flypaper trap on the roof and cover the front steps with super slippery soap in an attempt to burglar-proof their house. Common Core Reference: CCSS.MATH.CONTENT.7.G.B.6
Transcript Surface Area - combined straight edge objects
Home alone at last! Mom, Dad, Buster, and the rest of the MacCaulay family are all gone for the day, so Calvin is happy to have the house all to himself. But something about this van that's been parked across the street all morning is making Calvin skittish. Suddenly, he remembers a story he heard on the news about a kid who saved his family’s valuables from a couple of inept robbers. Although the robbers didn't get the family's stuff, they did get away. Calvin decides that he's not taking any chances: it's time to burglarproof the house! Luckily, Calvin has some supplies to foil the robbers' dastardly plan: Super-slick soap? Check. Industrial strength fly paper? Check. Luckily, Calvin is a master at calculating the area of faces of 3 dimensional shapes, so he doesn’t waste his supplies. The news said that the burglars like to enter through the chimney, just like Santa Claus, so the first trap Calvin wants to set is to completely cover the roof in fly paper. Look! The roof is in the shape of a square pyramid. It’s called a square pyramid because it has a square base. This one measures 45 feet by 45 feet, and the triangle faces each have a height of 25.5 feet, and meet at a point called the apex. We can plug these measurements into the formula for the area of a triangle to find the surface area of the roof. The area of a triangle equals one half times the base times the height. Plugging in the numbers for the base and the height, forty-five times 25.5 is 1,147.5. Dividing this by two gives us 573.75, and multiplying the result by 4 for the number of triangle faces, we get 2,295 square feet for the surface area of the roof. That's a lot of fly paper! Just in case the burglars decide to come through the front door, Calvin wants to cover the front steps in some super-slippery soap. The stairs are a composite shape composed of rectangular prisms. Remember, a prism is made up of faces that include two identical bases and flat sides. First, we divide the prisms into faces. Then, we add all the relevant areas together. Making up the faces of the rectangular prisms are 12 rectangles labeled 'A', each measuring 12 inches by 8 inches. The area of each rectangle is found by multiplying the length times the width. Then, we multiply the area of one rectangle by the total number of rectangles, 12. That gives us a total area of 1,152 square inches. For the sides of the prisms, there are 3 sides labeled 'B' with dimensions of 40 inches by 8 inches, and 3 tops labeled 'C', with dimensions 40 inches by 12 inches. All of these faces are rectangles, so we can calculate the surface area of each face by multiplying the length times the width. For the faces labeled B, we have 3 rectangles, each with the dimensions 40 inches times 8 inches which gives us 960 square inches. For the faces labeled C, we have 3 rectangles, each with the dimensions 40 inches times 12 inches, giving us 1,440 square inches. Now, just add the areas of the relevant faces together to get the total visible surface area. Calvin needs enough soap to cover 3,552 square inches. Getting back to Calvin, It looks like the booby traps have been set and Calvin is feeling pretty safe and secure. It must be the burglars! They’re going to find out they picked the wrong kid to mess with! Oops. Sorry! It looks like that was just the delivery guy's van parked across the street.
Surface Area - combined straight edge objects exercise
-
Find the surface area of the square pyramid.
HintsThe height of one of the triangles of the pyramid is the shortest distance from the apex of the pyramid to the base of the triangle.
The base of one of the triangles of the pyramid is the side of the triangle that is opposite the apex of the pyramid.
Pay attention to the units. An area is given by $ft^2$, or $in^2$, or ...
SolutionTo determine the whole area that has to be covered by sticky fly paper, we first have to decide the shape of the roof: it's a quadratic pyramid; i.e. a pyramid with a rectangular base.
Four triangles of equal dimensions make up the sides of the pyramid. So we have to determine the area of one of the triangles and then multiply it by four to get the area of all of the sides together.
Do you still know the formula for the area of a triangle? It's $A_{\text{triangle}}=\frac12(\text{base})(\text{height})$.
What is the base and the height? Just take a look at the picture beside. The base is $45~ft$ and the height is $25.5~ft$.
We plug these values into the formula above to get $A_{\text{triangle}}=\frac12(45)(25.5)=573.75~ft^2$, the area of one of the triangles.
We then have to multiply this value by $4$ to get the area of the whole roof: $A=4\times 573.75=2295~ft^2$.
-
Calculate the surface area of the staircase.
HintsJust use the formula $A_{\text{rectangle}}=(\text{length})(\text{width})$.
There are some rectangles of type $A$ on the other side of the staircase.
You have to add all calculated areas.
SolutionHow much of the super slippery soap does Calvin need?
Just take a look at the staircase; it's composed by different rectangles of type $A$, $B$, and $C$. For each type, we use the formula $A_{\text{rectangular}}=(\text{length})(\text{width})$.
Let's start with $A$:
- There are $6$ such rectangles visible to us. But, on the other side of the staircase, there another $6$. Together we have $12$ rectangles of type $A$.
- Each of those rectangles has the area $12\times 8=96~in^2$.
- We multiply this area by $12$ to get $12\times 96=1,152~in^2$.
- There are $3$ such rectangles.
- The area of one of these rectangles is $40\times 8=320~in^2$.
- This value has to multiplied by $3$ to get $3\times 320~in^2=960~in^2$.
- There are $3$ such rectangles.
- The area of one of them is $40\times 12=480~in^2$.
- Multiplying this by $3$ leads to $3\times 480~in^2=1,440~in^2$.
-
Determine the surface area of the triangular prism.
HintsUse the following formulas: $A_{\text{triangle}}=\frac12(\text{base})(\text{height})$ for a triangle, and $A_{\text{rectangle}}=(\text{length})(\text{width})$ for a rectangle.
An isosceles triangle has two legs with the same length. The rectangles with identical area have this length as the width and the height of the prism as the length.
SolutionTo wrap the present Calvin has for his family, he needs to make sure he has enough gift wrap. So first he has to determine the surface area of the triangular prism.
The prism is composed of $2$ isosceles triangles and $3$ rectangles.
Let's start with the triangles, which both are of equal size.
We take the formula,
$A_{\text{triangle}}=\frac12(\text{base})(\text{height})$,
and plug the given values for the base, $6~in$, and for the height, $4~in$, in to get $A_{\text{triangle}}=\frac12(6)(4)=12~in^2$ for each triangle.
We still have to double the area to get $24~in^2$.
Next we handle the rectangles: two of them have the same area. The two with the same area have identical width, $5~in$, and length, $15~in$.
We plug those values into the formula, $A_{\text{rectangular}}=(\text{length})(\text{width})$, to get $A_{\text{rectangular}}=(15)(5)=75~in^2$. We double it to $150~in^2$.
There is still one rectangle left with width $6~in$ and the length $15~in$.
So we get $A_{\text{rectangular}}=(15)(6)=90~in^2$.
Last we add all those areas together to get the area of the triangular prism: $24~+~150~+~90~=~265~in^2$.
-
Identify the formulas for surface areas of the different shapes.
HintsFirst decide which two dimensional shapes each three dimensional shape is composed of.
There are only two three dimensional shapes which are composed of only one type of two dimensional shape.
Here you see a trapezoid. Two sides, $b_1$ and $b_2$, are parallel. The distance of those sides is the height $h_T$ of the trapezoid.
The area formula is given by $A_{\text{trapezoid}}=\frac12(b_2+b_2)(h_T)$.
SolutionLet's start with the tetrahedron. It's only composed of triangles with area given by the formula,
$A_{\text{triangle}}=\frac12bh$.
Because the pyramid consists of four such triangles, we get that the area of the tetrahedron is $2\frac12bd=2bh$.
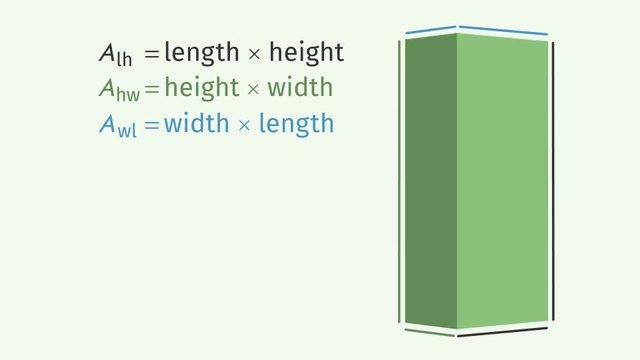
Next we have a rectangular prism, which is composed of rectangles with area equal to either $lw$, $lh$, or $wh$.
There are two rectangles with area $lw$, two with area $lh$, and two with area $wh$.
Adding these areas together, we get that the surface area of the rectangular prism is $2(lw+lh+wh)$.
The next shape is a prism with a trapezoid as the base. The area of the trapezoids is given by the formula,
$A_{\text{trapezoid}}=\frac12(b_2+b_2)(h_T)$,
where
- $b_1$ and $b_2$ are the lengths of the parallel sides, and
- $h_T$ is the height of the trapezoid, or distance between the parallel sides.
Adding the areas of the four rectangles and two trapezoids, we get that the surface area is $(b_2+b_2)(h_T)+(b_1+b_2+2s)l=(h_T+l)b_1+(h_T+l)b_2+2sl$.
The last shape is a pyramid with a square as the base. For this we need the formula for the area of a triangle as well as the formula for the area of a square with side length $a$:
$A_{\text{square}}=a^2$.
Together with the area formula for a triangle with height $h$, we can see that the area of the pyramid is $2ah+a^2$.
-
Recall the area formulas for a triangle and rectangle and find the areas of the ones displayed.
HintsYou get the values for each shape in the header. Just plug those values into the formula.
If you "cut" a rectangle along the diagonal into two, you get two triangles. Those triangles have the same area.
SolutionFor the calculations of different areas we need a few formulas:
The formula for the area of a triangle is $A_{\text{triangle}}=\frac12(\text{base})(\text{height})$.
So for the triangle given, the area is $A_{\text{triangle}}=\frac12(45)(25.5)=573.75$.
The formula for the area of a rectangle is $A_{\text{rectangular}}=(\text{length})(\text{width})$.
So for the rectangle given, the area is $A_{\text{rectangular}}=(40)(12)=480$.
-
Figure out the surface area of the sculpture.
HintsThe surface area of one of the sides of the bigger tetrahedron is given by subtracting the area of one of the smaller tetrahedron's sides.
Calculate the total surface area of the bigger tetrahedron, then subtract the area of one of the sides of the smaller one from this total. Then add the area of three of the sides of the smaller tetrahedron to get the surface area of the sculpture.
SolutionLet's start with the bigger tetrahedron: the $4$ triangles all have a base of $20~in$ and a height of $17.3~in$. Using the formula for the area of a triangle,
$A_{\text{triangle}}=\frac12(\text{base})(\text{height})$,
We get that the total area of the bigger tetrahedron is $4\times\frac12(20)(17.3)=692~in^2$.
The area of one of the sides of the smaller tetrahedron is $\frac12(5)(4.3)=10.75~in^2$.
Since only three of the sides of the smaller tetrahedron are included in the surface area of the sculpture, and that part of the surface area of one of the sides of the bigger tetrahedron is not included in the surface area of the sculpture, we have that the total surface area of the sculpture is $(692-10.75)+(3\cdot 10.75)=713.5~in^2$.