Solving Quadratic Equations by Taking Square Roots

Basics on the topic Solving Quadratic Equations by Taking Square Roots
We will learn on how to factor the difference of two squares. Like 4x² – 25 = 0, for example. When factoring such a difference of two squares, we end up always getting the product of the sum and the difference of the same two terms. For instance, with 4x² – 25 = 0, we end up taking the square roots of 4x² and 25 to get 2x and 5, respectively. Then 2x and 5 are the terms which appear in our product. In other words, the factorization of 4x² – 25 = 0 is (2x + 5)(2x – 5) = 0, or (2x – 5)(2x + 5) = 0, as the commutative property of real numbers states that order of factors in multiplication or addition does not matter. To know more about this method for factoring the difference of two squares, you can watch this video.
This method for factoring the difference of two squares can be represented in algebraic expressions as follows:
Product of Sum and Difference of Two Squares: (a + b)( a – b) = a² – b²
Factors of Difference of Two Squares: a² – b² = (a + b)(a – b)
where a and b are any real numbers.
Solve quadratic equations in one variable.
CCSS.MATH.CONTENT.HSA.REI.B.4.B
Transcript Solving Quadratic Equations by Taking Square Roots
Welcome back! Let’s join our game, already in progress. It’s time to play “The Difference of Two Squares”! Okay, it’s Phillip and Lara’s turn and they choose Dr. Evil's square. Okay, Dr. Evil, the question is: How do you factor x2 - 64 = 0? Dr. Evil says the answer is (x + 8)(x -8) = 0 and Phillip and Lara agree. They’re correct and get the square! And Round 1 goes to Phillip & Lara! Let’s take another look at the game-winning question.
Factoring Equations
They were asked to solve x2 - 64 = 0, which is the difference of two squares. Let’s see how they did it: First, set up your two factors like this: ( + )( - ) = 0. Then, plug square roots into the blanks. Next, complete the parentheses with the square roots of the two terms from the binomial. Plug in the square root of the first term, x², in the first place in the parentheses and the root of the second term -- disregard the minus sign -- in the second place. At last, just simplify the expressions and the equation is factored.
Now let’s join them in the bonus round already in progress. It’s Keith and Jasmine’s turn. They’re looking to come back from behind in this game. They need a block, so they pick Rapunzel. Okay, Rapunzel, your question is to factor 16x4 - 81 = 0. Rapunzel says the answer is (4x² + 9)(4x² - 9) = 0. Keith & Jasmine take a moment to talk it over and yes!!! They agree with Rapunzel. They're correct! And Keith & Jasmine win the square! What a block!
But Phillip and Lara can win the game here! Phillip and Lara pick the Dark Count’s square in hopes of ending this Bonus Round with a win. The Dark Count’s question is 49 - x⁶ = 0. Dark Count, how do you factor this one? That's a tricky one, but the Dark Count looks confident and says the answer is (7 + x³)(7 - x³) = 0. Phillip and Lara discuss the question and it looks like, yes, they do agree which is exactyl correct! Phillip and Lara win the square...and the GAME!!! Whew! that last round went quickly! Let's take a look at that again in slow motion. There were three critical points to the two teams' success.
Difference of two Squares
Let's start with a normal quadratic function: ax² + bx + c = 0. To be a difference of two squares, the 'b' coefficient must be 0 leaving us with ax² + c = 0. The coefficients 'a' and 'c' may not have the same sign. The exponent must be an even number. So let's change this plus to a minus, leaving us with ax² - c = 0. Since it's also possible that 'a' is negative and 'c' is positive, we could also see the binomial expression in the form c - ax² = 0. Keith & Jasmine had to factor a doozey of a binomial when they got 16x⁴ - 81 = 0.
But they kept their cool and set up their solution. Keith and Jasmine set up the solution the way they were taught. Now they just need to place the square root of each term of the binomial into the proper place. The square root of 16 is 4 and the square root of 'x' to the fourth is 'x' squared, making the first term for each set of parentheses 4x squared. Since the square root of 81 is 9, Keith and Jasmine write 9 in the second place of each set of parentheses and plugged in the numbers into their solution, giving them (4x² + 9)(4x² - 9) = 0.
Not to be outdone, Phillip and Lara also had a bit of a curve ball thrown their way with the expression 49 - x⁶ = 0. They went down their checklist, point by point. The 'b' coefficient must be 0, check. The coefficients 'a' and 'c' may not have the same sign, check. The exponent must be an even number, check. With all the boxes checked, they set up their solution, but with a slight twist. They use their knowledge of exponents to get their second term, +/- x³. It is just the square root of x⁶. So they plug in that number.
Zero Product Property
Then, they took the square root of 49 and plugged that answer in as well. Perfect! Remember, ladies and gents, you can solve all of these equations by simply using the Zero Product Property! Simply set each of the parentheses equal to zero and solve using PEMDAS!
Let’s join our players and crown our winner for today! Phillip and Lara seem to be enjoying a relaxing afternoon on the beach.
Solving Quadratic Equations by Taking Square Roots exercise
-
Explain how to factor quadratic equations which are a difference of two squares.
HintsThe quadratic equation $x^2-4=0$ is a difference of two squares.
To solve $x^2-4=0$, first write this equation as follows:
$(\sqrt{~~~}+\sqrt{~~~})(\sqrt{~~~}-\sqrt{~~~})=0$.
Next put $x^2$ as well as $4$ under the square root sign:
$(\sqrt{x^2}+\sqrt{4})(\sqrt{x^2}-\sqrt{4})=0$.
Simplifying, we get:
$(x+2)(x-2)=0$.
SolutionIn order for such a quadratic equation to be a difference of two squares, it must meet the following requirements:
- The coefficient $b$ must be zero.
- The coefficient $a$ and $c$ must have different signs.
- The exponent must be even.
- $b=0$ $~~~~~$ ✓
- $a=16$ and $c=-81$ $~~~~~$ ✓
- The exponent is $2$ $~~~~~$ ✓
$(\sqrt{~~~}+\sqrt{~~~})(\sqrt{~~~}-\sqrt{~~~})$.
Next put $16x^2$ as well as $81$ under the square root sign:
$(\sqrt{16x^2}+\sqrt{81})(\sqrt{16x^2}-\sqrt{81})=0$.
Now take the square root of the terms above to get
$(4x+9)(4x-9)=0$.
Lastly solve this equation using the zero product property; either we have that $4x+9=0$ or $4x-9=0$.
-
Factor the quadratic equation.
HintsThe goal is to get an equation which looks like
$(e+f)(e-f)=0$.
Using the FOIL method of multiplication, you get
$e^2-f^2=0$.
Backwards, you have to do the following: first assign
- $e^2=x^2$
- $f^2=64$
SolutionTo factor Dr. Evil's equation, we first have to check to see if it is a difference of two squares. Keeping the standard form $ax^2+bx+c=0$ of a quadratic equation in mind, we check the following:
- $b=0$? $~~~~~$✓
- $a$ and $c$ must have different signs: $a=1$ and $c=-64$ $~~~~~$✓
- The exponent has to be even. And, sure, it is, namely $2$. $~~~~~$✓
First rewrite the left side of the equation as the product of two binomials:
$(\sqrt{~~~}+\sqrt{~~~})(\sqrt{~~~}-\sqrt{~~~})=0$.
Next put $x^2$ and $64$ under the square root sign:
$(\sqrt{x^2}+\sqrt{64})(\sqrt{x^2}-\sqrt{64})=0$.
Lastly take the square root to get:
$(x+8)(x-8)=0$.
To solve the equation we use the zero product property as well as opposite operations:
Either we have
$\begin{array}{rcl} x+8 & = & ~0\\ \color{#669900}{-8} & &\color{#669900}{-8}\\ x & = & ~-8 \end{array}$
or
$\begin{array}{rcl} x-8 & = & ~0\\ \color{#669900}{+8} & &\color{#669900}{+8}\\ x & = & ~8 \end{array}$
-
Find the errors in Rap-Punzel's calculations.
HintsWrite the difference as the product of two binomials
$(\sqrt{(~~~)^2}+\sqrt{(~~~)^2})(\sqrt{(~~~)^2}-\sqrt{(~~~)^2})=0$.
Take the square root. Let's have a look at a few examples:
- $\sqrt{36}=6$
- $\sqrt{x^2}=x$
- $\sqrt{x^6}=x^3$
- ...
If you have to take the square root of a product you can multiply the square roots of the factors.
SolutionIf you have the difference of two squares, you can factor as follows:
$e^2-f^2=(e+f)(e-f)$.
Let's consider a few examples:
$4x^2-9=0$.
Write the left side as the product of two binomials. We write
$(\sqrt{4x^2}+\sqrt{9})(\sqrt{4x^2}-\sqrt{9})=0$.
Then you can take the square root to get:
$(4x+3)(4x-3)=0$.
In a similar manner you can factor the following examples:
- $25-x^4=0$ $\rightarrow$ $(\sqrt{25}+ \sqrt{x^4})(\sqrt{25}-\sqrt{x^4})=0$, and by taking the square root we get $(5+x^2)(5-x^2)=0$.
- $25x^2-36=0$ $\rightarrow$ $(\sqrt{25x^2}+ \sqrt{36})(\sqrt{25x^2}-\sqrt{36})=0$, and by taking the square root we get $(5x+6)(5x-6)=0$.
- $49x^6-121=0$ $\rightarrow$ $(\sqrt{49x^6}+ \sqrt{121})(\sqrt{49x^6}-\sqrt{121})=0$, and by taking the square root we get $(7x^3+11)(7x^3-11)=0$.
-
Identify which factorizations of the equations are correct.
HintsLook at the example
$16x^4-36=0$.
First write as
$(\sqrt{16x^4}+\sqrt{36})(\sqrt{16x^4}-\sqrt{36})=0$.
Then take the square roots to get
$(4x^2+6)(4x^2-6)=0$.
If you have to take the square root of a product, you can take the square root of each factor and multiply those square roots after.
You can also check the factorization using the FOIL method for multiplication:
$(4x^2+6)(4x^2-6)=(4x^2)(4x^2)-(4x^2)(6)+(6)(4x^2)-(6)(6)=16x^4-36$ $~~~~~$✓
SolutionAll the equations have in common, that the regarding left side is the difference of two squares. So you can factor them as follows:
- $9x^2-9=0$ $\rightarrow$ $(\sqrt{9x^2}+ \sqrt{9})(\sqrt{9x^2}-\sqrt{9})=0$ and by taking the square root we get $(3x+6)(3x-6)=0$; the answer was correct.
- $x^6-100=0$ $\rightarrow$ $(\sqrt{x^6}+ \sqrt{100})(\sqrt{x^6}-\sqrt{100})=0$ and by taking the square root we get $(x^3+10)(x^3-10)=0$; the answer was wrong, because $\sqrt{x^6}=x^3$ instead of $x^2$.
- $100-16x^2=0$ $\rightarrow$ $(\sqrt{100}+ \sqrt{16x^2})(\sqrt{100}-\sqrt{16x^2})=0$ and by taking the square root we get $(10+4x)(10-4x)=0$; the answer was wrong. Keep in mind to take the square root for both factors.
- $9x^6-144=0$ $\rightarrow$ $(\sqrt{9x^6}+ \sqrt{144})(\sqrt{9x^6}-\sqrt{144})=0$ and by taking the square root we get $(3x^3+12)(3x^3-12)=0$; the answer was correct.
- $49x^2-64=0$ $\rightarrow$ $(\sqrt{49x^2}+ \sqrt{64})(\sqrt{49x^2}-\sqrt{64})=0$ and by taking the square root we get $(7x+8)(7x-8)=0$; the answer was correct.
-
Explain any differences between $16x^4 -81=0$ and $ax^2 +bx +c=0$.
HintsCompare the terms step by step.
$x$ is the variable.
Another example for such an equation is
$16x^4+81=0$.
SolutionLet's check the differences between the two equations:
- The degree, or largest exponent value of $x$ in a term, for $16x^4 -81=0$ is $4$ and for $ax^2 +bx +c=0$ is $2$.
- There is no term in $16x^4 -81=0$ of the form $bx$. This means that $b=0$.
- Normally $a$ and $b$ could have all possible values, except $a=0$, and also a positive as well as a negative sign. For $16x^4 -81=0$, $a=16$ and $c=-81$ have different signs.
-
Determine the factored equation.
Hints$4x^6-36=0$ is equivalent to
$(2x^3+6)(2x^3-6)=0$.
You still have to take the square root of the corresponding terms.
The square root of a power with an even exponent is the power with the same base and the half the value of the exponent:
$\sqrt{x^{2n}}=x^n$
SolutionEach time you have to factor an equation, where the left side is the difference of two squares, you can write the left side as follows:
$(\sqrt{~~~}+\sqrt{~~~})(\sqrt{~~~}-\sqrt{~~~})$,
and put the corresponding terms under the square root sign after.
Let's try it with $169x^4-144=0$. We have
$(\sqrt{169x^4}+\sqrt{144})(\sqrt{169x^4}-\sqrt{144})=0$.
Now take the square root to get
$(13x^2+12)(13x^2-12)=0$.
Let's try it again with $81-36x^2=0$. We have
$(\sqrt{81}+\sqrt{36x^2})(\sqrt{81}-\sqrt{36x^2})=0$.
Again we take the square root to get
$(9+6x)(9-6x)=0$.
Just one last example: $121-16x^8=0$.
Keeping the square root of a product in mind, $\sqrt{36x^2}=\sqrt{36}\times\sqrt{x^2}=6x$, we have
$(\sqrt{121}+\sqrt{16x^8})(\sqrt{121}-\sqrt{16x^8})=0$.
Now we take the square root
$(11+4x^4)(11-4x^4)=0$.
What are Quadratic Functions?
Graphing Quadratic Functions
FOILing and Explanation for FOIL

Solving Quadratic Equations by Taking Square Roots
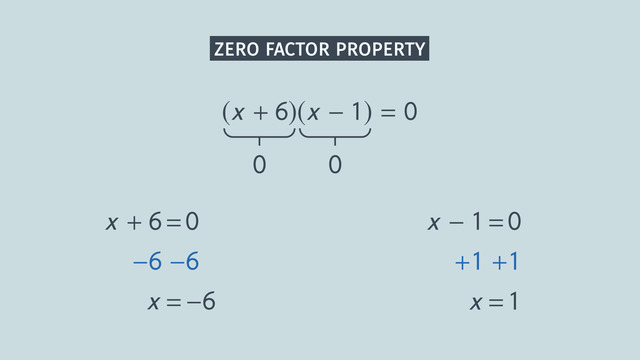
Solving Quadratic Equations by Factoring
Factoring with Grouping

Solving Quadratic Equations Using the Quadratic Formula

Solving Quadratic Equations by Completing the Square
Finding the Value that Completes the Square
Using and Understanding the Discriminant
Word Problems with Quadratic Equations








