How to Order Fractions?
Basics on the topic How to Order Fractions?
Ordering Fractions
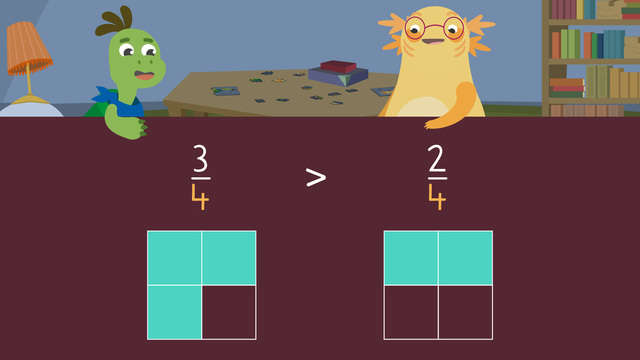
When you see two fractions in front of you, it can sometimes be hard to determine how these fractions are related to one another. We can compare and order fractions with different or unlike denominators by translating these fractions into equivalent fractions with common denominators and then we can use symbols < (less than) or > (more than) to compare them. We can also put fractions in order from least to greatest (ascending) or from greatest to least (descending) depending on the question.
Equivalent Fractions – Definition
Let’s revise what fractions and equivalent fractions are first:
Fractions always represent a part of a whole. For example if a pizza is divided into eight equal pieces, one piece is called $\frac{1}{8}$ of a whole pizza.
Equivalent fractions are fractions which have the same value but they are represented with a different numerator and denominator.
Comparing Fractions – Examples
We can look at the example below for a better understanding: both fractions $\frac{1}{3}$ and $\frac{4}{12}$ are fractions with different numerators and denominators but have the same value as the shaded purple area is the same on both diagrams.
Comparing and ordering fractions with different denominators from least to greatest means that we must translate the fractions into equivalent fractions first.Then we can compare the numerators to order them in ascending or descending order.
Let’s look at the examples below.
The fraction on the left has a denominator of three and the fraction on the right has a denominator of six.
For three and six the common multiple that the both numbers share is twelve. Now we need to multiply the numerator and denominator of the fraction on the left hand side by four (4) to get to a common denominator. The fractions on the right needs to be multiplied by two (2). So our two equivalent fractions for $\frac{1}{3}$ and $\frac{3}{6}$ are $\frac{4}{12}$ and $\frac{6}{12}$ .
Since we have found the common denominator, we can now compare. For this, we can look at numerators and decide which number is smaller. We use less than symbol (<) as 4 is less than 6 , so $\frac{1}{3}$ is less than $\frac{3}{6}$.
Ordering Fractions – Examples
When we have more than two fractions with different denominators and different numerators, we must find a common denominator first and then compare the numerators again. In order to find the common denominator, we have to find the multiple that the fractions share. Let’s look at the example below: We will compare three fractions this time: $\frac{2}{3}$, $\frac{1}{2}$ and $\frac{4}{5}$. We would like to order those three fractions in ascending order from least to greatest. The common denominator here is 30. Next,we translate all the fractions to have the denominator of 30. The first fraction $\frac{2}{3}$ must be multiplied both by ten (10). The second fraction $\frac{1}{2}$ must be multiplied by fifteen (15), and the last fraction $\frac{4}{5}$ must be multiplied by six (6). Remember to multiply both the denominator and the numerator if you want to order and compare fractions.
Since we have found all three equivalent fractions we are looking at denominators to compare them and decide which fraction is the smallest and which fraction is the biggest. 15 is the smallest numerator and the biggest is 24. So now, we can order them from least to greatest: $\frac{15}{30}$ is less than $\frac{20}{30}$ and $\frac{20}{30}$ is less than $\frac{24}{30}$ . So, we can say that $\frac{1}{2}$ is less than $\frac{2}{3}$ and $\frac{2}{3}$ is less than $\frac{4}{5}$. ½ < ⅔ < ⅘
Comparing and Ordering Fractions – Summary
Today we learned how to compare fractions and ordering fractions with different or unlike denominators. Let’s review our knowledge and remember all steps in correct order:
| Step # | Comparing fractions | Ordering fractions |
|---|---|---|
| 1 | Create an equivalent fraction with common denominators | Create an equivalent fraction with common denominators |
| 2 | Rewrite all fractions with the new common denominators | Rewrite all fractions with the new common denominators |
| 3. | Multiply the denominators and numerators by the same number |
Multiply the denominators and numerators by the same number |
| 4 |
Compare numerators and use > (greater than) or < (less than) symbols to state which fraction is bigger or smaller |
Put all fractions in ascending or descending order looking at numerators |
To test your knowledge on comparing and ordering fractions with different denominators, have a look at our videos, worksheets and quiz.
Transcript How to Order Fractions?
“The water glistens on the cave walls tonight.” “Tank, I think this machine is broken.” “We’ll have to get a new one.” We can help Axel find the best deal on a new karaoke machine by… “Ordering Fractions”. We can compare and order fractions with unlike denominators... by creating equivalent fractions with common denominators. An equivalent fraction is a fraction that has the same value but is represented with a different numerator and denominator. Let’s use three-fourths and five-sixths as an example. First, we rename each fraction with a common denominator. To find the common denominator of fractions, we need to think of a multiple that they share. What is one number that is a multiple of BOTH four and six? Twenty-four. This number becomes the denominator for both fractions. To rename the numerators, we multiply the numerator by the SAME number that we multiplied the original denominator by. In three-fourths, we multiply the denominator, four, by six to make twenty-four, so we will also multiply the numerator by six. What is three times six? Eighteen. Three-fourths is the same as eighteen twenty-fourths. In five-sixths, we multiply the six by four to make twenty-four, so we will multiply the five by four. What is five times four? Twenty. Five-sixths is the same as twenty-twenty-fourths. Once we have like denominators, we can order the fractions from least to greatest by looking at the numerators. Eighteen is less than twenty, so three-fourths is less than five-sixths. Axel sees ads for three stores selling karaoke machines. Each store is running a sale with the machine being a fractional amount off the regular price. If we make equivalent fractions and order them, we’ll determine which store has the biggest discount. We have two-thirds, one-half, and four-fifths. First, think of a multiple that three, two, AND five share. Thirty is a multiple that can be made with all three numbers. Now, rewrite all the denominators as thirty. Next, rename the numerators, by multiplying them by the SAME number that we multiplied the original denominator by. Let’s start with the store with two-thirds off the price. What do we multiply three by to make thirty? Ten… so we will multiply the numerator, two, by ten. What is two times ten? Twenty. Two-thirds and twenty-thirtieths are equivalent. In one-half, what do we multiply two by to make thirty? Fifteen. We will multiply the numerator, one, by fifteen and get fifteen. One-half and fifteen-thirtieths are equivalent. Finally, in four-fifths, what do we multiply five by to make thirty? Six. What is six times, the numerator, four? Twenty-four. Four-fifths and twenty-four thirtieths are equivalent. What do we do next? We compare the numerators and order the fractions from least to greatest. The order of the numerators from least to greatest is fifteen, twenty, and twenty-four, so we order the fractions as one-half is less than two-thirds is less than four-fifths. The store with four-fifths off the price has the biggest discount. As Axel and Tank make their purchase, let’s review. Remember… we can compare and order fractions with unlike denominators by creating equivalent fractions with common denominators. First, we rename each fraction with a common denominator. To rename the numerators, we multiply it by the SAME number that we needed to multiply to make the denominator. Once we have like denominators, we can order the fractions from least to greatest by looking at the numerators. We can write the original fractions as an expression using less than or greater than symbols. “The water glistens on the cave walls tonight.” “No fish can be seen.” singing beautifully] “I’m in an aquarium of solitude…” “ and it appears….I’m the KING!” "Ebb and FLOW, ebb and Flow..." "That's so beautiful!"
How to Order Fractions? exercise
-
Match equivalent fractions by multiplying by 4.
HintsAlways multiply the numerator and the denominator by the same number. For this problem the numerator and denominator are both being multiplied by 4.
In this example, both the numerator and denominator are multiplied by 6. This creates the equivalent fraction, $\frac{18}{24}$.
Solution- $\frac{1}{5}$ = $\frac{4}{20}$, because when the numerator and denominator in $\frac{1}{5}$ are both multipled by 4 we get $\frac{4}{20}$.
- $\frac{1}{4}$ = $\frac{4}{16}$, because when the numerator and denominator in $\frac{1}{4}$ are both multipled by 4 we get $\frac{4}{16}$.
- $\frac{1}{3}$ = $\frac{4}{12}$, because when the numerator and denominator in $\frac{1}{3}$ are both multipled by 4 we get $\frac{4}{12}$.
- $\frac{2}{6}$ = $\frac{8}{24}$, because when the numerator and denominator in $\frac{2}{6}$ are both multipled by 4 we get $\frac{8}{24}$.
-
Find the equivalent fractions.
Hints2 fractions are equivalent to $\frac{1}{2}$, and 2 fractions are equivalent to $\frac{1}{3}$.
To see if 2 fractions are equivalent, find a multiple the denominators share. Then multiply the numerator by the same to see if the fractions are equivalent. Example: $\frac{4}{16}$ and $\frac{1}{4}$
Both 4 and 16 fit into 16
4 x $\frac{1}{4}$ = $\frac{4}{16}$
$\frac{4}{16}$ = $\frac{4}{16}$
The fractions are equivalent.Multiply $\frac{1}{2}$ and $\frac{1}{3}$ by 5, 4, and 3 to find the equivalent fractions.
Solution- $\frac{1}{2}$ = $\frac{5}{10}$, because when the numerator and denominator in $\frac{1}{2}$ are both multipled by 5 we get $\frac{5}{10}$.
- $\frac{1}{2}$ = $\frac{4}{8}$, because when the numerator and denominator in $\frac{1}{2}$ are both multipled by 4 we get $\frac{4}{8}$.
- $\frac{1}{3}$ = $\frac{3}{9}$, because when the numerator and denominator in $\frac{1}{3}$ are both multipled by 3 we get $\frac{3}{9}$.
- $\frac{1}{3}$ = $\frac{4}{12}$, because when the numerator and denominator in $\frac{1}{3}$ are both multipled by 4 we get $\frac{4}{12}$.
-
Find the equivalent fractions.
HintsFind a number that the numerator and denominator on the left can be multiplied by, to make another fraction on the right.
For example, if we multiply $\frac{4}{5}$ by 2, we would get $\frac{8}{10}$. Or if we multiplied $\frac{4}{5}$ by 3 we would get $\frac{12}{15}$.
What is $\frac{2}{5}$ x 1? Or $\frac{2}{5}$ x 2? Eventually, you will find the equivalent fraction.
You're multiplying the fractions on the left by 2, 3 and 5.
SolutionThe above image shows the equivalent fractions. To find each equivalent pair:
- $\frac{1}{2}$ = $\frac{5}{10}$ because when the numerator and denominator in $\frac{1}{2}$ are both multipled by 5 we get $\frac{5}{10}$.
- $\frac{2}{5}$ = $\frac{4}{10}$ because when the numerator and denominator in $\frac{2}{5}$ are both multipled by 2 we get $\frac{4}{10}$.
- $\frac{3}{4}$ = $\frac{9}{12}$ because when the numerator and denominator in $\frac{3}{4}$ are both multipled by 3 we get $\frac{9}{12}$.
- $\frac{3}{6}$ = $\frac{9}{18}$ because when the numerator and denominator in $\frac{3}{6}$ are both multipled by 3 we get $\frac{9}{18}$.
-
Ordering fractions.
HintsAll of the denominators on the right are 50. Think about how the numerator and denominator in the fraction on the left can be multiplied to make a new fraction with a denominator of 50.
Look at the first question, $\frac{3}{5}$ . Find what factor the denominator (5) in $\frac{3}{5}$ needs to be multiplied by to make 50.
Next, multiply the numerator (3) by this same factor.
The top number in the fraction is the numerator.
The bottom number in the fraction is the denominator.
Solution- 1) $\frac{3}{5}$ x $\frac{10}{10}$ = $\frac{30}{50}$.
- 2) $\frac{2}{25}$ x $\frac{2}{2}$ = $\frac{4}{50}$
- 3) $\frac{4}{10}$ x $\frac{5}{5}$ = $\frac{20}{50}$
-
Complete the numerator.
HintsAll of the choices have the same denominator, 20. What multiplied by 5 makes 20? You must also multiply the numerator by this number.
To find the equivalent fraction, solve for the numerator.
Find the answer for 20 ÷ 5, then multiply the numerator (3) by the same number.Multiply the numerator and denominator by 4.
Solution- 5 x 4 = 20
- 3 x 4 = 12
- $\frac{12}{20}$ is an equivalent fraction to $\frac{3}{5}$
-
Ordering different denominators.
HintsFirst, find a common multiple of all fractions.
Try multiplying the largest denominator by 2, and see if the product is a number that is a common multiple of the other fractions.
- Next, create equivalent fractions with the same denominator.
- Finally, order the fractions from least to greatest.
6, 4, 8 and 12 are all common multiples of 24. Convert the fractions to have a denominator of 24.
Solution- $\frac{1}{6}$ x $\frac{4}{4}$ = $\frac{4}{24}$
- $\frac{1}{4}$ x $\frac{6}{6}$ = $\frac{6}{24}$
- $\frac{3}{8}$ x $\frac{3}{3}$ = $\frac{9}{24}$
- $\frac{5}{12}$ x $\frac{2}{2}$ = $\frac{10}{24}$